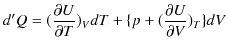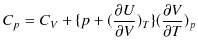Chapter2 熱力学第一法則(エネルギー法則)
2.1 熱と仕事
歴史的に見て,熱量と仕事(エネルギー)は別物だと考えられていて,熱量の単位には ![]() が使われていました.ここで,
が使われていました.ここで,![]() は水
は水 ![]() を
を ![]() 上昇させるのに必要な熱量です.一方,仕事(エネルギー)の単位には
上昇させるのに必要な熱量です.一方,仕事(エネルギー)の単位には ![]() (ジュール) が使われます.熱がエネルギーの一種であることを初めて確認したのはジュールです.ジュールは羽根車を使った実験で,仕事
(ジュール) が使われます.熱がエネルギーの一種であることを初めて確認したのはジュールです.ジュールは羽根車を使った実験で,仕事 ![]() と熱量
と熱量 ![]() の間に,次の関係を見出しました.
の間に,次の関係を見出しました.
ここで,
![]() を仕事当量といいます."熱" のChapterの冒頭で述べたように,現代では,熱がエネルギーであることは,熱の本質であると認識されています.今後の記述においては,熱の単位として
を仕事当量といいます."熱" のChapterの冒頭で述べたように,現代では,熱がエネルギーであることは,熱の本質であると認識されています.今後の記述においては,熱の単位として ![]() を使うことで統一します.
を使うことで統一します.
2.2 熱力学第一法則
物体の巨視的状態で決定される量を状態量といいます.状態量には物体の分量に関係のない示強変数と,物体の分量に比例する示量変数があります.示強変数の例としては,圧力 ![]() ,絶対温度
,絶対温度 ![]() などがあり,示量変数の例としては,体積
などがあり,示量変数の例としては,体積 ![]() ,内部エネルギー
,内部エネルギー ![]() などが挙げられます.
などが挙げられます.
内部エネルギーとは,文字通り物体の内部の状態によって決まるエネルギーですが,分子運動論的に考えると,その内容が明確になります.すなわち,内部エネルギーは,物体を構成している原子・分子の運動エネルギーと,原子・分子間の結合力に関係したポテンシャルによって決定されます.特に,気体のように分子間力が弱く,ポテンシャルが無視できる場合は,内部エネルギーは各分子の運動エネルギーの総和と考えることができます.
ここで,内部エネルギー ![]() を変化させるのに,2つの方法があることに注意しましょう.1つは電熱器やバーナーの火で熱するように,熱
を変化させるのに,2つの方法があることに注意しましょう.1つは電熱器やバーナーの火で熱するように,熱 ![]() を加える方法です.もう1つはジュールの実験や摩擦を加える場合などのように仕事
を加える方法です.もう1つはジュールの実験や摩擦を加える場合などのように仕事 ![]() を加える方法です.いずれも内部エネルギー
を加える方法です.いずれも内部エネルギー ![]() は増加します.(逆に,熱
は増加します.(逆に,熱 ![]() を奪う,あるいは仕事
を奪う,あるいは仕事 ![]() をさせる場合もあります.この場合は,内部エネルギー
をさせる場合もあります.この場合は,内部エネルギー ![]() は減少します.)このとき,前のSectionで見たように熱もエネルギーの一種であり,広い意味でのエネルギー保存則が成立します.すなわち,次の熱力学第一法則が成立します.
は減少します.)このとき,前のSectionで見たように熱もエネルギーの一種であり,広い意味でのエネルギー保存則が成立します.すなわち,次の熱力学第一法則が成立します.
法則2.1(熱力学第一法則1) "熱力学的状態変化に伴う内部エネルギーの変化量
![]() は,熱
は,熱 ![]() によるエネルギーの移動と,力学的仕事
によるエネルギーの移動と,力学的仕事 ![]() によるエネルギーの移動の総和になります."
によるエネルギーの移動の総和になります."
このことを式で表してみます.すなわち,状態1(内部エネルギー ![]() )から,状態2(内部エネルギー
)から,状態2(内部エネルギー ![]() )へ変化したとき,内部エネルギーの変化量
)へ変化したとき,内部エネルギーの変化量
![]() は,
は,
となります.このとき,内部エネルギーは状態量ですので,内部エネルギーの変化量
![]() は,状態1と状態2のみで決定され,変化の過程に依りません.一方,
は,状態1と状態2のみで決定され,変化の過程に依りません.一方,![]() と
と ![]() は非状態量です.例えば,状態1から状態2への変化を熱
は非状態量です.例えば,状態1から状態2への変化を熱 ![]() だけで行うことができます.または,同じ変化を仕事
だけで行うことができます.または,同じ変化を仕事 ![]() だけで行うこともできます.あるいは,熱
だけで行うこともできます.あるいは,熱 ![]() と仕事
と仕事 ![]() の組み合わせで行うこともできます.
の組み合わせで行うこともできます.
古来より,人類は外から何もエネルギーを供給せずに働く機関を夢見てきました.このような機関を第一種永久機関といいます.熱力学第一則はエネルギー保存則ですが,第一種永久機関は,明らかに熱力学第一法則に反しています.言い直すと熱力学第一法則とは,
法則2.2(熱力学第一法則2) "第一種永久機関は存在しません."
ということができます.
2.3 準静変化
熱力学においては,物体の状態が変化する場合を取り扱わねばなりません.そこで,物体が常に熱平衡の状態を保つように,ゆっくりとした変化を考えます.このような状態変化を準静変化といいます.準静変化はもとに戻すことができるので可逆変化です.力学的現象において,摩擦や空気抵抗がないような理想的な状況では,可逆変化が起こることが知られています.一方,熱力学においては,可逆変化といえば主に準静変化になります.
物体に熱を加えて(あるいは奪って),可逆的な準静変化を起こす場合を考えます.この場合,熱源といわれるものを使います.熱源は,物体の絶対温度と無限小だけ異なる絶対温度をもち,物体に接触させて熱をやり取りします.その際,物体の絶対温度は変化することもありますが,熱源はきわめて大きいので,その絶対温度は変わらないものとします.物体に微小な熱を加える,あるいは奪う場合,その量を,
と表すことができます.ダッシュを付けたのは,熱が非状態量であり,増加とか減少とかで言い表せるものではなく,ただ小さい熱ということを表すためです. 物体に仕事を加えて(あるいは仕事をされて),可逆的な準静変化を起こす場合を考えます.これは,物体を圧縮したり,膨張させたりする場合に相当します.仕事の量が微小な場合,それを,
と表すことができます.ダッシュを付けたのは,仕事が非状態量であり,増加とか減少とかで言い表せるものではなく,ただ小さい仕事ということを表すためです.
ここで,図のように,シリンダーの中に気体を入れ,ピストンで蓋をしている場合を考えましょう.
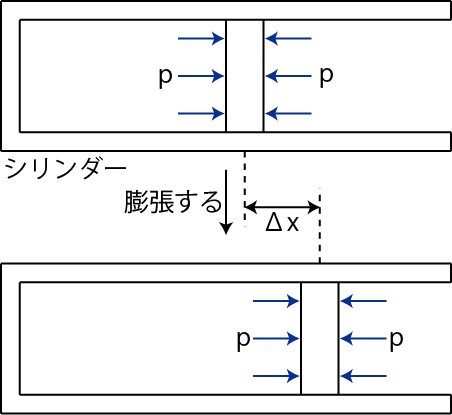
Figure2.1: 仕事1
準静変化の場合,シリンダー内部の気体の圧力と外部からの圧力はつりあいながらピストンはゆっくりと移動します.つりあっている圧力 ![]() が一定の場合を考えます.このとき,中の気体のする仕事
が一定の場合を考えます.このとき,中の気体のする仕事 ![]() は,
は,
となります.ただし,![]() はピストンの断面積であり,
はピストンの断面積であり,
![]() は体積変化量です.一方,外から気体に加えた仕事
は体積変化量です.一方,外から気体に加えた仕事 ![]() は,(外部からの圧力による力
は,(外部からの圧力による力 ![]() の向きとピストンの移動の向きが逆なので,膨張の場合,負の仕事になります.)
の向きとピストンの移動の向きが逆なので,膨張の場合,負の仕事になります.)
となります.上の2式は圧縮の場合にも成立します.(圧縮の場合は,
![]() になります.)
になります.)
それでは,圧力が変化する場合,気体のする仕事 ![]() ,外から気体に加えた仕事
,外から気体に加えた仕事 ![]() を求めましょう.
を求めましょう.
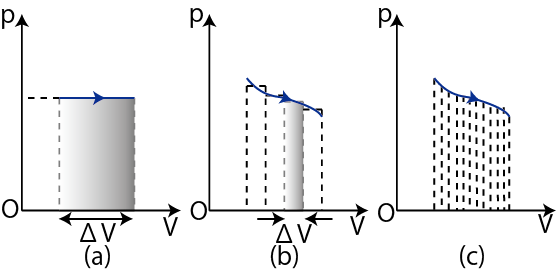
Figure2.2: 仕事2
圧力が一定の場合,![]() グラフは
グラフは ![]() が一定で,
が一定で,![]() 軸に平行な直線になりますが,気体のする仕事
軸に平行な直線になりますが,気体のする仕事![]() は,このグラフの長方形の面積になります.(図(a)を参照して下さい.)一般に,圧力が変化する場合では,グラフをある短い間隔
は,このグラフの長方形の面積になります.(図(a)を参照して下さい.)一般に,圧力が変化する場合では,グラフをある短い間隔
![]() で幾つかの区間に分割します.その区間において圧力の平均値をとり,有限個の長方形をつくります.各区間において,気体のする仕事
で幾つかの区間に分割します.その区間において圧力の平均値をとり,有限個の長方形をつくります.各区間において,気体のする仕事
![]() は長方形の面積で近似されます.したがって,全体の気体のする仕事
は長方形の面積で近似されます.したがって,全体の気体のする仕事 ![]() は長方形の面積の和となります.(図(b)を参照して下さい.)ここで,
は長方形の面積の和となります.(図(b)を参照して下さい.)ここで,
![]() を無限小にする極限をとります.無限個の細長い長方形でグラフは分割され,グラフのでこぼこはなくなり,気体のする仕事
を無限小にする極限をとります.無限個の細長い長方形でグラフは分割され,グラフのでこぼこはなくなり,気体のする仕事 ![]() は,無限個の細長い長方形の面積,
は,無限個の細長い長方形の面積,
の和になります.(図(c)を参照して下さい.)(このとき,微小区間での外から気体にする仕事は,
となります.)つまり,圧力が変化する場合でも,気体のする仕事 ![]() は,
は,![]() グラフの面積であり,これは圧力
グラフの面積であり,これは圧力 ![]() を体積
を体積 ![]() で積分したものです.故に,気体のする仕事
で積分したものです.故に,気体のする仕事 ![]() は,次式で表せます.
は,次式で表せます.
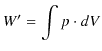
また,外から気体にした仕事 ![]() は,
は,
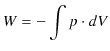
です.
熱力学第一法則(2.1)式を無限小の可逆的な準静変化の場合について書き直し,微分形式で表現すると,
となることがわかります.ここで,![]() だけが状態量でした.さらに,(2.2)式に,
だけが状態量でした.さらに,(2.2)式に,
を代入すると,
が成立します.
2.4 定積変化と定圧変化
これから,2つのSectionにおいて,理想気体の特徴のある4つの状態変化について取り扱うことにします.いずれの状態変化も準静変化であるとします.
まず,体積を一定にして行う状態変化(定積変化といいます.)を考えましょう.状況は図の通りです.
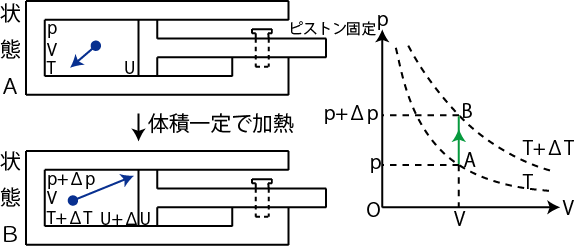
Figure2.3: 定積変化
この場合,ピストンが動かないので,気体がする仕事は ![]() です.
です.
外からの仕事も ![]() です.
です.
したがって,熱力学第一法則(2.1)式,
は,
となります.内部エネルギーは加えた熱の分だけ増加します.(逆に,熱を奪ったときは,内部エネルギーはその分減少します.)
次に,圧力を一定にして行う状態変化(定圧変化といいます.)を見ておきましょう.状況は図の通りです.
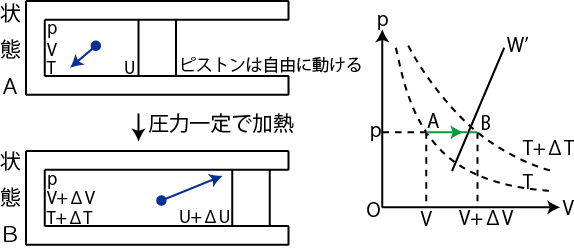
Figure2.4: 定圧変化
この場合,前のSectionの結果より,
が成立します.熱力学第一法則(2.1)式,
は,
となります.内部エネルギーは加えた熱の分だけ増加し,外に仕事をする分だけ減少します.(逆に,熱を奪ったときは,内部エネルギーは減少し,外から仕事をされたときは,内部エネルギーは増加します.)
物質 ![]() 当たり,絶対温度を
当たり,絶対温度を ![]() 上昇させるのに必要な熱量をモル比熱といいます.定積変化の場合のモル比熱(定積モル比熱といいます.)は,
上昇させるのに必要な熱量をモル比熱といいます.定積変化の場合のモル比熱(定積モル比熱といいます.)は,
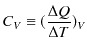
であり,定圧変化の場合のモル比熱(定圧モル比熱といいます.)は,
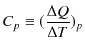
で,それぞれ定義されます.ここで,右下の添え字は一定の状態量を表します.また,これらの定義式では物質量 ![]() で割るべきですが,物質が
で割るべきですが,物質が ![]() の場合を考えて,
の場合を考えて,![]() で割ることは省略しました.(以下,このSectionでは気体が1[mol]ある場合を考えます.)ここで,内部エネルギー
で割ることは省略しました.(以下,このSectionでは気体が1[mol]ある場合を考えます.)ここで,内部エネルギー ![]() を状態量
を状態量 ![]() と
と ![]() の関数であるとみなし,
の関数であるとみなし,
と書くことにします.(理想気体の場合,状態量 ![]() については状態方程式で関係付けられます.)内部エネルギー
については状態方程式で関係付けられます.)内部エネルギー ![]() は状態量であり,全微分で書くことができます.故に,
は状態量であり,全微分で書くことができます.故に,
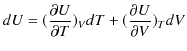
が成立します.前のSectionの関係式(2.3)式,
より,
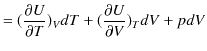 |
ですから,
となります.定積変化の場合,![]() なので,(2.4)式より,
なので,(2.4)式より,
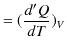 |
||
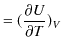 |
が成り立ちます.理想気体では,定積モル比熱
![]() は温度に依らないと考えてよいので,
は温度に依らないと考えてよいので,
となります.この式は定積変化を考えて導きましたが,同じ温度変化を定圧変化で起こしても,同じ式が成立します.一般に,理想気体では内部エネルギー ![]() は絶対温度
は絶対温度 ![]() のみの関数であり,圧力
のみの関数であり,圧力 ![]() と体積
と体積 ![]() に依存しません.このことは統計力学から説明されます.
に依存しません.このことは統計力学から説明されます.
また,(2.4)式で圧力 ![]() を一定にして,
を一定にして,![]() で偏微分し,定圧モル比熱
で偏微分し,定圧モル比熱
![]() を求めます.
を求めます.
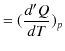 |
||
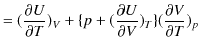 |
よって,
となります.ここで,上で説明したように,内部エネルギー ![]() は体積
は体積 ![]() に依存しないので,
に依存しないので,
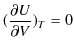
となります.また,![]() の理想気体については,状態方程式,
の理想気体については,状態方程式,
が成立します.この式の両辺を絶対温度 ![]() で偏微分して,
で偏微分して,
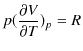
となります.したがって,(2.5)式は次のようになります.
よって,
です.(2.6)式はマイヤーの関係といわれ,気体の種類に依らずに成立します.
内部エネルギー ![]() ,圧力
,圧力 ![]() ,体積
,体積 ![]() から,
から,
により定義される関数 ![]() をエンタルピーといいます.エンタルピー
をエンタルピーといいます.エンタルピー ![]() の全微分を表すと,
の全微分を表すと,
となります.ここで,(2.3)式,
を代入して計算すると,次のようになります.
ここで,定圧変化の場合を考えると,![]() なので,
なので,
となり,よって,
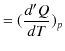 |
||
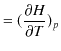 |
が成立します.
2.5 等温変化と断熱変化
3つ目の理想気体の可逆的準静変化として,絶対温度が一定の状態変化である等温変化を取り扱ってみましょう.状況は図の通りです.
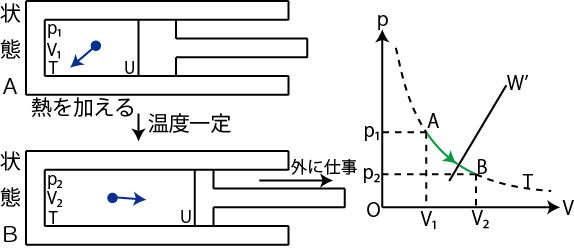
Figure2.5: 等温変化
絶対温度が一定なので,ボイルの法則,
が成立します.故に,![]() グラフは双曲線になります.また,絶対温度が一定なので,内部エネルギーの変化はありません.式で書くと,
グラフは双曲線になります.また,絶対温度が一定なので,内部エネルギーの変化はありません.式で書くと,
です.したがって,熱力学第一法則(2.1)式,
は,
となります.加えた熱の分,気体は外に仕事をします.(逆に,外から仕事をされた場合は,その分だけ熱を放出します.)ここで,気体がする仕事 ![]() は,
は,![]() グラフの面積ですが,次のように計算されます.
グラフの面積ですが,次のように計算されます.
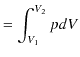 |
||
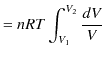 |
||
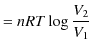 |
ここで,等温変化のとき,
が成立したので,加えた熱 ![]() は,
は,
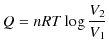
になります.
4つ目の理想気体の可逆的準静変化として,気体が外部と熱のやりとりをしない,断熱変化を取り扱ってみます.状況は図の通りです.
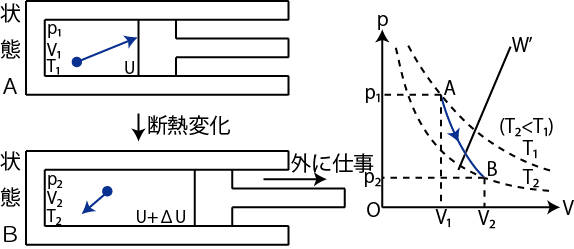
Figure2.6: 断熱変化
断熱変化の特徴を式で表せば,
です.したがって,熱力学第一法則(2.1)式,
は,
となります.つまり,気体が外に仕事をした分,内部エネルギーが減少します.(逆に,外から仕事をした場合は,その分,内部エネルギーが増加します.)したがって,体積が増加する断熱膨張の場合,内部エネルギーが減少し,絶対温度が下がります.体積が減少する断熱圧縮の場合,内部エネルギーが増加し,絶対温度が上昇します.ここで,無限小の可逆的準静変化の断熱変化を考えてみましょう.無限小の変化についての熱力学第一法則(2.3)式,
より,
となります.理想気体では,
が成り立ち,状態方程式より,
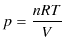
なので,上式は次のように変形されます.
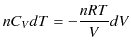 |
||
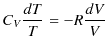 |
||
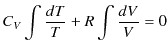 |
||
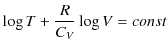 |
ただし,定積モル比熱
![]() は,温度に依存しないことを使いました.ここで,マイヤーの関係(2.6)式,
は,温度に依存しないことを使いました.ここで,マイヤーの関係(2.6)式,
より,
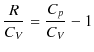
です.ここで,比熱比 ![]() を,
を,
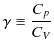
で定義すると,上式は,
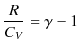
となります.よって,
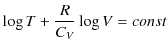
は,次のように変形されます.
ここで,状態方程式より,
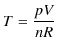
なので,
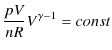 |
||
となります.最後の式をポアソンの式といいます.
2.6 カルノーサイクル
ここで,4つの状態変化と関連して,熱機関というものを取り扱っておきます.熱機関とは,熱を仕事に変える装置のことをいいます.熱機関の概念を示します.
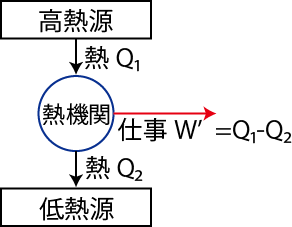
Figure2.7: 熱機関
熱機関の具体例としては,自動車のエンジンなどが挙げられます.このような熱機関で用いられる物質を作業物質といいますが,自動車のエンジンの場合はガソリンが使われます.そして,その状態は気体です.エンジンでは,気体がある1つの状態 ![]() から出発して,再びその状態
から出発して,再びその状態 ![]() に戻るような状態変化を繰り返しています.この1周りの状態変化をサイクルといいます.サイクルで1周りすると,内部エネルギーの変化量は
に戻るような状態変化を繰り返しています.この1周りの状態変化をサイクルといいます.サイクルで1周りすると,内部エネルギーの変化量は ![]() なので,熱力学第一法則(2.1)式,
なので,熱力学第一法則(2.1)式,
より,(熱機関は高熱源から熱
![]() をもらい,その一部を低熱源に熱
をもらい,その一部を低熱源に熱
![]() だけ捨てます.(
だけ捨てます.(
![]() ))
))
となります.(気体は外に仕事
![]() をします.)その際,もらった熱
をします.)その際,もらった熱 ![]() に対する,外にした仕事
に対する,外にした仕事
![]() の比を熱効率といいます.すなわち,熱効率
の比を熱効率といいます.すなわち,熱効率 ![]() は次式で定義されます.
は次式で定義されます.
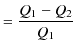 |
熱機関の最も簡単で理想的なものとして,理想気体を作業物質として使い,可逆的な準静変化である等温変化と断熱変化を組み合わせたカルノーサイクルというものを考えましょう.カルノーサイクルの ![]() グラフは図の通りです.
グラフは図の通りです.
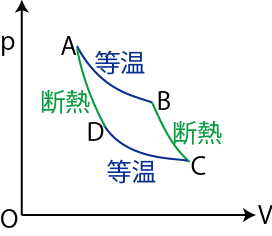
Figure2.8: カルノーサイクル
A→B: 高熱源(絶対温度 ![]() )に接し,熱平衡を保ちながら,準静的に等温膨張します.熱
)に接し,熱平衡を保ちながら,準静的に等温膨張します.熱 ![]() を吸収します.
を吸収します.
B→C: 準静的に断熱膨張して,低熱源の絶対温度 ![]() まで下げます.
まで下げます.
C→D: 低熱源(絶対温度 ![]() )に接し,熱平衡を保ちながら,準静的に等温圧縮します.熱
)に接し,熱平衡を保ちながら,準静的に等温圧縮します.熱 ![]() を放出します.
を放出します.
D→A: 準静的に断熱圧縮して,高熱源の絶対温度 ![]() まで上げます.
まで上げます.
ここで,気体のする仕事を考えましょう.状態変化
![]() の間に,その
の間に,その ![]() グラフの下の部分の面積だけ,気体は外から仕事をします.また,状態変化
グラフの下の部分の面積だけ,気体は外から仕事をします.また,状態変化
![]() の間に,その
の間に,その ![]() グラフの下の部分の面積だけ,気体は外から仕事をされます.したがって,差し引き1サイクルの間に気体がする仕事
グラフの下の部分の面積だけ,気体は外から仕事をされます.したがって,差し引き1サイクルの間に気体がする仕事 ![]() は,
は,![]() グラフの面積
グラフの面積 ![]() です.カルノーサイクルは現実のエンジンにはなりませんが,熱力学の様々な議論をする際,極めて重要です.特に,次のChapterで見ていく熱力学第二法則に関して,かかわりが深いです.また,カルノーサイクルの状態変化は,全て可逆的な準静変化です.したがって,逆周りのサイクルが考えられます.これを逆カルノーサイクルといいます.逆カルノーサイクルでは,低熱源から
です.カルノーサイクルは現実のエンジンにはなりませんが,熱力学の様々な議論をする際,極めて重要です.特に,次のChapterで見ていく熱力学第二法則に関して,かかわりが深いです.また,カルノーサイクルの状態変化は,全て可逆的な準静変化です.したがって,逆周りのサイクルが考えられます.これを逆カルノーサイクルといいます.逆カルノーサイクルでは,低熱源から
![]() の熱が奪われ,高熱源に
の熱が奪われ,高熱源に
![]() の熱が放出されます.(
の熱が放出されます.(
![]() )その結果,逆カルノーサイクルは,外から仕事
)その結果,逆カルノーサイクルは,外から仕事
![]() をされます.このように,逆カルノーサイクルは低熱源を冷やす働きがあります.
をされます.このように,逆カルノーサイクルは低熱源を冷やす働きがあります.