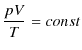Part1 熱力学の成立

Chapter1 熱

1.1 熱の本質

熱の本質は原子・分子のランダムな熱運動にあります．その意味で熱は原子物理学と関係しています．歴史的に見て，熱素という熱の性質をもった物質の存在も考えられましたが，現在では否定されています．熱運動を示す現象としては，煙が拡散していく現象やブラウン運動などが知られています．どちらの現象も原子・分子が熱運動をしていて，それが微粒子に衝突することが原因になっています．原子・分子の熱運動の力学的エネルギー（運動エネルギーとポテンシャル）の総和が熱です．したがって，熱はエネルギーの一種であり，熱エネルギーという言い方もします．

　また，全ての物質は固体・液体・気体の三態をとりますが，それらの違いは熱運動の激しさによって決定されます．固体の状態は原子・分子が振動している（固体は結晶をつくっていて，その各格子点を中心に原子・分子が振動しています．），液体の状態は原子・分子が動き回っている，気体の状態は原子・分子が飛びまわっていると表現されます．

 

1.2 温度

熱運動の激しさ（熱運動による原子・分子の運動エネルギー）を表すのが温度です．1気圧のもとで，水と氷が共存する温度を $ 0[^{\circ}C]$ とし，水が沸騰する温度を $ 100[^{\circ}C]$ として，その間を100等分した温度をセルシウス温度といいます．日常生活で使われる温度はセルシウス温度です．

　温度を下げていくと，熱運動の程度が低くなっていきますが，セルシウス温度で $ -273.15[^{\circ}C]$ で熱運動が停止します．（厳密に言うと量子力学的には零点振動をしていますが，ここでは考えません．）この温度を絶対零度といいます．自然界には，絶対零度よりも低い温度は存在しません．絶対零度を基準とし，温度差1度がセルシウス温度と等しくなるように定めた温度を絶対温度といい，単位にはケルビン $ [K]$ を用います．絶対温度 $ T[K]$ とセルシウス温度 $ t[^{\circ}C]$ の間には，次の関係が成立します．

$\displaystyle T=t+273.15$

 

温度

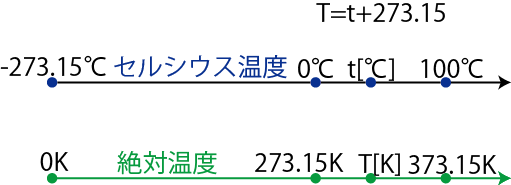
Figure1.1: 温度

 

1.3 熱量

高温物体Aと低温物体Bとを接触させると，次第にAの温度が下がり，Bの温度が上がります．やがて両者の温度は等しくなり，それ以後，温度は変わらなくなります．このような状態を熱平衡にあるといいます．このとき，熱運動のエネルギーがAからBへ移っています．これをAからBへ熱が移動したといい，移動した熱の量を熱量 $ Q$ といいます．熱量はエネルギーですので単位はジュール $ [J]$を使います．また，この場合，熱量の保存という次の関係が成立します．

　（高温物体Aが失った熱量）＝（低温物体Bが得た熱量）

この関係は，Aが失った熱量が移動し，それがそのままBに流れ込むことを考えれば理解できます．また，熱平衡に関して，次の熱力学第0法則が成立します．

法則1.1(熱力学第0法則) "物体Aと物体Bが熱平衡にあり，物体Aと物体Cが熱平衡にあれば，BとCも熱平衡の状態にあります．"

このことは当然のように思えますが，実験によってはじめて確かめられることです．

　物体の温度を同じだけ上昇させるために必要な熱量は，物体によって異なり，多くの熱量が必要な物体程，温まりにくい物体といえます．ある物体の絶対温度を $ 1[K]$ だけ上昇させるのに必要な熱量を，その物体の熱容量といいます．熱容量 $ C$ の物体の絶対温度を， $ \Delta T[K]$ だけ変化させるために必要な熱量 $ Q[J]$ は次式で与えられます．

$\displaystyle Q=C\cdot\Delta T$

この式から，熱容量Cの単位は $ [J/K]$であることがわかります．また，単位質量の物体の絶対温度を $ 1[K]$ だけ上昇させるのに必要な熱量を比熱といいます．比熱 $ c$ の物質からなる質量 $ m[g]$ の物体の温度を， $ \Delta T[K]$ だけ変化させるために必要な熱量 $ Q[J]$ は次式で与えられます．

$\displaystyle Q=mc\cdot\Delta T$

この式から，比熱 $ c$ の単位は $ [J/g\cdot K]$ であることがわかります．熱容量 $ C[J/K]$ と比熱 $ c[J/g\cdot K]$ の関係は次式になります．

$\displaystyle C=mc$

 

1.4 気体の法則

このSectionでは，気体の熱的性質について述べることにします．まず，気体の圧力について言及します．気体に圧力があることを示す例としては，ゴム風船が挙げられます．中に入っている気体の圧力により，ゴム風船は膨らみます．気体の圧力の原因は，やはり気体分子の熱運動にあります．非常に多くの気体分子が何度もゴム風船の壁に衝突し，その衝撃の総和が気体の圧力になっています．気体の圧力の単位には，パスカル $ [Pa]=[N/m^{2}]$ を使用します．身の回りの空気も圧力を生じています．これを大気圧といいます．地上における大気圧の大きさを $ 1[atm]$（アトム）といいます．$ 1[atm]$ を他の単位で表すと次のようになります．

$\displaystyle 1[atm]=1.013\times10^{5}[Pa]=760[mmHg]$

$ 760[mmHg]$ とは，常温で液体の金属である水銀の $ 760[mm]$ 分の高さの圧力と，大気圧がつりあうことから使われている単位です．このことは，トリチェリが実験によって示しました．また，普段大気圧をほとんど意識することなく生活していますが，これは大気圧が物体の外側から働くのと同時に，内側からも働いていて力がつりあっていることが原因です．

　気体の熱的性質に関しては，その状態を表す3つの物理量が問題となります．1つ目は気体の圧力 $ p[Pa]$，2つ目は気体の体積 $ V[m^{3}]$，3つ目は気体の絶対温度 $ T[K]$ です．この気体の状態を表す3つの物理量の間に成立する関係が気体の法則です．以下に，その内容を見ていくことにします．

　1つ目の法則はボイルの法則です．その内容は，

法則1.2(ボイルの法則) "絶対温度が一定の場合，一定質量の気体の体積 $ V[m^{3}]$ は圧力 $ p[Pa]$ に反比例します．"

というものです．このことを式で表せば，

$\displaystyle pV=const$

となります．ボイルの法則は気体分子運動の観点から，直観的に理解することができます．

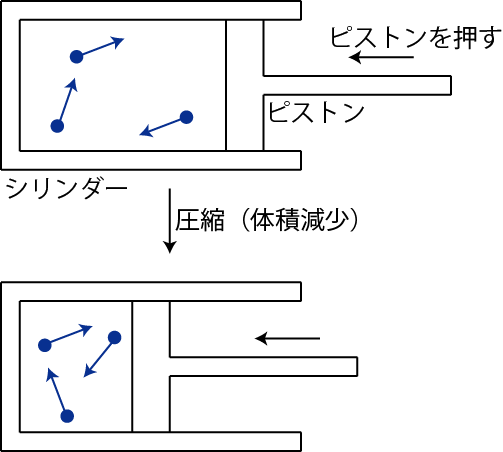
ボイルの法則

Figure1.2: ボイルの法則

絶対温度が一定の場合，分子の熱運動の激しさは変わりません．ピストンに力を加え圧縮し，体積を減らした場合，分子が壁と衝突する頻度が増加します．分子と壁との衝突が気体の圧力の原因なので，体積が減少したとき，気体の圧力は増大することになります．

　2つ目の法則はシャルルの法則です．その内容は，

法則1.3(シャルルの法則) "圧力が一定の場合，一定質量の気体の体積 $ V[m^{3}]$ は絶対温度 $ T[K]$ に比例します．"

というものです．このことを式で表せば，

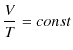
$\displaystyle \dfrac{V}{T}=const$

となります．シャルルの法則は気体分子運動の観点から直観的に理解することができます．

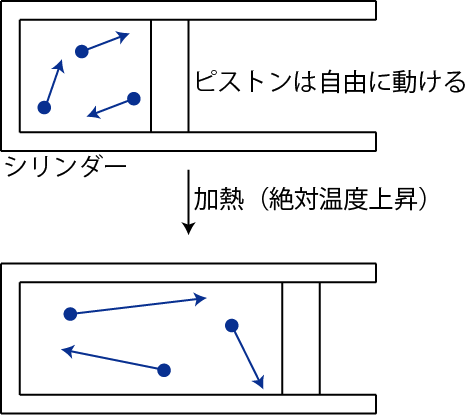
シャルルの法則1

Figure1.3: シャルルの法則1

ピストンを自由に動けるようにしておくと，大気圧と中の気体の圧力がつりあい，中の気体の圧力は一定に保たれます．そのようにしておいて，加熱すると絶対温度が上昇し，分子の熱運動が激しくなります．したがって，圧力を一定にするとき，体積が増大することになります．シャルルの法則について，$ V-T$ グラフを描くと次のようになります．

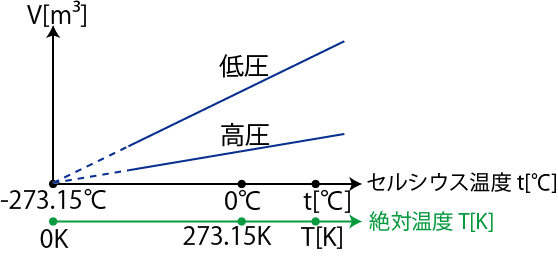
シャルルの法則2

Figure1.4: シャルルの法則2

この図からわかるように，シャルルの法則を適用するときには，必ず絶対温度を使用しなければなりません．セルシウス温度を使うと，$ V$ と$ t$ は一次関数の関係になってしまい，状況が複雑になってしまうからです．また，極低温においては物質が液体になってしまい，シャルルの法則が成立しません．（グラフでは，その部分を破線で描いておきました．）

　ボイルの法則とシャルルの法則を併せたものが，ボイル-シャルルの法則です．その内容は次のように表せます．

法則1.4(ボイル-シャルルの法則) "一定質量の気体の体積 $ V[m^{3}]$ は，絶対温度 $ T[K]$ に比例し，圧力 $ p[Pa]$ に反比例します．"

このことを，式で表せば，

$\displaystyle \dfrac{pV}{T}=const$ (1.1)

となります．ボイル-シャルルの法則に従う気体のことを理想気体といいます．実在する気体はよい近似で理想気体ですが，極低温や超高圧など，ある条件の下では理想気体からずれてきます．

　それでは，さらにボイル-シャルルの法則を変形しておきましょう．アボガドロの法則，

法則1.5(アボガドロの法則) "同温・同圧のもとで，同体積の気体は，種類によらず，同数個の分子を含みます．"

が成立するので，同温・同圧の下では，同じ物質量 $ n[mol]$ の気体の体積は，種類によらず一定になります．ここで，ボイル-シャルルの法則(1.1)式において，右辺の $ const$ は物質量 $ n[mol]$ に比例することに注意します．例えば，圧力 $ p[Pa]$ と絶対温度 $ T[K]$ が一定ならば，体積 $ V[m^{3}]$ を増加させると物質量 $ n[mol]$ が増えます．また，体積 $ V[m^{3}]$ と絶対温度 $ T[K]$ が一定ならば，圧力 $ p[Pa]$ を増加させると，物質量 $ n[mol]$ が増えます．したがって，

$\displaystyle const=nR$

とおけます．ただし，$ R$ は比例定数です．このとき，ボイル-シャルルの法則(1.1)式は，

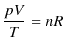
$\displaystyle \dfrac{pV}{T}=nR$

すなわち，

$\displaystyle \fbox{pV=nRT}$ (1.2)

となります．この(1.2)式を理想気体の状態方程式といいます．また，比例定数 $ R$ のことを気体定数といいますが，標準状態（ $ 0[^{\circ}C]=273.15[K],1[atm]=1.01325\times10^{5}[Pa]$）において，気体の体積は $ 1[mol]$ 当たり， $ 2.24139\times10^{-2}[m^{3}/mol]$ であることを使って，その値を求めます．このとき，(1.2)式より，

$\displaystyle 1.01325\times10^{5}[Pa]\times2.24139\times10^{-2}[m^{3}]=1[mol]\times R\times273.15[K]$

ですから，計算すると，

$\displaystyle R$ $\displaystyle =\dfrac{1.01325\times10^{5}\times2.24139\times10^{-2}[J]}{1[mol]\times273.15[K]}$    
  $\displaystyle \cong8.31[J/mol\cdot K]$    

となります．