が成立します.図の熱機関全体で考えると,
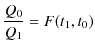
が成立することになります.以上の3つの式より,
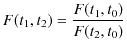 |
の関係が得られます.ここで,![]() は
は
![]() を満たす限り,任意の値をとることができるので,それを
を満たす限り,任意の値をとることができるので,それを ![]() とおき,
とおき,
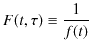
で定義される関数 ![]() を導入します.このとき,
を導入します.このとき,
理想的な力学的現象において,理論上可逆変化が存在することは,よく知られています.今まで述べてきたように,熱力学においても理想的な可逆的準静変化は理論上存在します.しかし,現実の世界を考えてみましょう.力学的現象においては,空気抵抗や摩擦が原因の熱の発生による不可逆的な現象が大半を占めます.また,熱力学においても熱伝導や摩擦熱等,不可逆的な現象がほとんどです.これら不可逆変化に関する法則を熱力学第二法則といいます.熱力学第二法則は3つの表現をとります.ここで,まとめておきます.
法則3.1(熱力学第二法則1(クラウジウスの原理)) "外に何も変化を与えずに,熱を低温から高温へ移すことは不可能です."
法則3.2(熱力学第二法則2(トムソンの原理)) "外から熱を吸収し,これを全部力学的な仕事に変えることは不可能です.(第二種永久機関は存在しません.熱効率 ![]() .)"
.)"
法則3.3(熱力学第二法則3(エントロピー増大の法則)) "不可逆断熱変化では,エントロピーは必ず増大します."
熱力学第二法則は経験則です.つまり,日常的な経験と直観的に矛盾しない内容になっています.そして,他の物理法則と同じように,多くの事象から帰納されたことが根拠となって,法則が成立しています.トムソンの原理において,第二種永久機関とは,外から熱を吸収し,これを全部力学的な仕事に変える機関のことをいいます.つまり,第二種永久機関とは,熱力学第二法則に反する機関です.これが実現すると,例えば,海水の内部エネルギーを吸収し,それを力学的仕事に変えて航行する船をつくることができます.しかし,熱力学第二法則は,これが不可能であることを言っています.
エントロピー増大の法則については,この後のSectionで詳しく取り扱うことにして,ここではクラウジウスの原理とトムソンの原理が同等であることを証明しておきましょう.証明の方法として,背理法を採用します.まず,クラウジウスの原理が正しくないと仮定します.この状況でカルノーサイクルを稼働し,高熱源から ![]() の熱を吸収し,低熱源に
の熱を吸収し,低熱源に ![]() の熱を放出させます.このカルノーサイクルは,熱力学第一法則より,
の熱を放出させます.このカルノーサイクルは,熱力学第一法則より,
の仕事を外にします.ここで,何の変化も残さずに熱は低熱源から高熱源へ移動できるので,![]() だけ移動させます.そうすると,低熱源の変化が打ち消されて,高熱源の熱
だけ移動させます.そうすると,低熱源の変化が打ち消されて,高熱源の熱
![]() が全部力学的な仕事になることになります.つまり,トムソンの原理が正しくないことになります.逆に,トムソンの原理が正しくないと仮定しましょう.この状況では,低熱源の
が全部力学的な仕事になることになります.つまり,トムソンの原理が正しくないことになります.逆に,トムソンの原理が正しくないと仮定しましょう.この状況では,低熱源の ![]() は全て力学的仕事にすることができます.この仕事により,逆カルノーサイクルを稼働することにします.ここで,仕事は全部逆カルノーサイクルを稼働することに使われたので,外には何の変化も与えません.低熱源から熱
は全て力学的仕事にすることができます.この仕事により,逆カルノーサイクルを稼働することにします.ここで,仕事は全部逆カルノーサイクルを稼働することに使われたので,外には何の変化も与えません.低熱源から熱 ![]() を吸収すると,1サイクル後,
を吸収すると,1サイクル後,
![]() の熱が低熱源から高熱源に移動したことになります.つまり,クラウジウスの原理は正しくないことになります.以上の議論により,2つの原理の同等性が証明されたことになります.
の熱が低熱源から高熱源に移動したことになります.つまり,クラウジウスの原理は正しくないことになります.以上の議論により,2つの原理の同等性が証明されたことになります.
カルノーサイクルは理想的な準静的可逆機関ですが,現実の熱機関は不可逆機関です.可逆機関と不可逆機関の熱効率について,次のカルノーの定理が成立します.
定理3.1(カルノーの定理1) "不可逆機関の熱効率は,同じ高熱源と低熱源との間に働く可逆機関の熱効率よりも小さくなります."
定理3.2(カルノーの定理2) "可逆機関ではどんな作業物質のときでも,高熱源と低熱源の絶対温度が等しければ,その熱効率は全て等しくなります."
それでは,熱力学第2法則を使ってカルノーの定理を証明します.そのために,下図のように高熱源と低熱源の間に,可逆機関である逆カルノーサイクル ![]() と不可逆機関
と不可逆機関 ![]() を稼働する状況を設定します.
を稼働する状況を設定します.
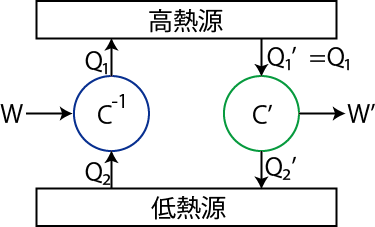
Figure3.1: カルノーの定理
可逆機関 ![]() の熱効率を
の熱効率を ![]() とし,低熱源からもらう熱を
とし,低熱源からもらう熱を ![]() ,高熱源に放出する熱を
,高熱源に放出する熱を ![]() ,外からされる仕事を,
,外からされる仕事を,
とします.(
![]() )不可逆機関
)不可逆機関 ![]() の熱効率を
の熱効率を ![]() とし,高熱源からもらう熱を
とし,高熱源からもらう熱を ![]() ,低熱源に放出する熱を
,低熱源に放出する熱を ![]() ,外にする仕事を,
,外にする仕事を,
とします.(
![]() )熱機関を適当に設定すれば,
)熱機関を適当に設定すれば,
とすることができるので,ここでは簡単のため,そのようにしておきます.このとき,高熱源には何の変化も起こりません.この系全体として,外にした仕事 ![]() は,
は,
となります.また,系全体として,低熱源に放出された熱
![]() は,
は,
です.ここで,
となりますが,
![]() は低熱源から吸収する熱を意味します.
は低熱源から吸収する熱を意味します.![]() ならば,系全体で低熱源から
ならば,系全体で低熱源から
![]() の熱をもらい,高熱源は変化なしで外に仕事をすることになります.これは,明らかに熱力学第二法則のトムソンの原理に反します.したがって,
の熱をもらい,高熱源は変化なしで外に仕事をすることになります.これは,明らかに熱力学第二法則のトムソンの原理に反します.したがって,![]() でなければなりません.故に,
でなければなりません.故に,
![]() なので,
なので,
となります.この不等式の両辺を
![]() で,辺々割ると,
で,辺々割ると,
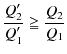
となります.ここで,
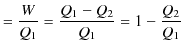 |
||
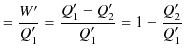 |
ですから,すなわち,
なので,
となります.故に,定理3.1が証明されました.次に,定理3.2を証明します.上図の系で不可逆機関 ![]() を可逆的なカルノーサイクルに置き換えます.そして,逆カルノーサイクル
を可逆的なカルノーサイクルに置き換えます.そして,逆カルノーサイクル ![]() を不可逆機関に取り換え,2つの熱機関の役割を入れ換えます.同様な議論により,
を不可逆機関に取り換え,2つの熱機関の役割を入れ換えます.同様な議論により,
が導出されます.元の状況と,2つの熱機関の役割を入れ換えた状況のいずれの場合についても,不可逆機関を可逆機関にすれば,2つの不等式が両立します.したがって,
が成立します.(証明終.)
カルノーの定理より,可逆機関の熱効率は,2つの熱源の温度だけで決定されることがわかります.温度 ![]() の高熱源から熱
の高熱源から熱 ![]() を吸収し,温度
を吸収し,温度
![]() の低熱源に熱
の低熱源に熱 ![]() を放出するとき,その間で働く可逆機関の熱効率
を放出するとき,その間で働く可逆機関の熱効率 ![]() は,
は,
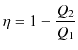
でした.これが2つの熱源の温度だけで決まるということは,ある関数 ![]() を用いて,
を用いて,
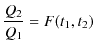
という関係が成立することになります.ここで,第3の熱源を考え,その温度を
![]() )とします.
)とします.![]() の熱源から
の熱源から ![]() を減らして,
を減らして,![]() の熱源に
の熱源に ![]() だけ増大させる可逆機関を考えると,
だけ増大させる可逆機関を考えると,
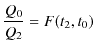
が成立します.図の熱機関全体で考えると,
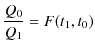
が成立することになります.以上の3つの式より,
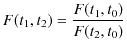 |
の関係が得られます.ここで,![]() は
は
![]() を満たす限り,任意の値をとることができるので,それを
を満たす限り,任意の値をとることができるので,それを ![]() とおき,
とおき,
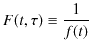
で定義される関数 ![]() を導入します.このとき,
を導入します.このとき,
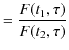 |
||
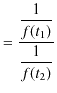 |
||
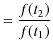 |
となります.関数 ![]() は可逆機関の性質からは決定することはできません.ただ,高熱源と低熱源の温度差が大きいほど熱効率が大きくなることから,
は可逆機関の性質からは決定することはできません.ただ,高熱源と低熱源の温度差が大きいほど熱効率が大きくなることから,![]() が増加すると
が増加すると ![]() の値も増加するという性質をもつことが確認できます.関数
の値も増加するという性質をもつことが確認できます.関数 ![]() が不定性をもっているので,最も簡単になるように温度を度盛ることを考えます.すなわち,
が不定性をもっているので,最も簡単になるように温度を度盛ることを考えます.すなわち,
とおくことにします.この ![]() を熱力学的絶対温度といいます.はじめにとった温度が摂氏であれ,華氏であれ,この式より熱力学的絶対温度に変換されることになります.これを用いると,
を熱力学的絶対温度といいます.はじめにとった温度が摂氏であれ,華氏であれ,この式より熱力学的絶対温度に変換されることになります.これを用いると,
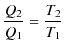
が導かれ,熱効率 ![]() は次式で表されます.
は次式で表されます.
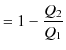 |
||
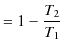 |
||
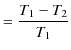 |
熱力学的絶対温度が,理想気体の状態方程式の絶対温度と一致することを確かめておきましょう.可逆機関であるカルノーサイクルは,等温変化と断熱変化を組み合わせたものであった.前のChapterの等温変化と断熱変化のSectionより,![]() の等温変化で高熱源(絶対温度
の等温変化で高熱源(絶対温度 ![]() )からもらう熱
)からもらう熱 ![]() は,
は,
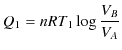
です.また,同様に ![]() の等温変化で低熱源(絶対温度
の等温変化で低熱源(絶対温度 ![]() )に放出する熱
)に放出する熱 ![]() は,
は,
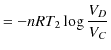 |
||
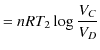 |
です.故に,カルノーサイクルの熱効率 ![]() は次のように計算されます.
は次のように計算されます.
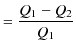 |
||
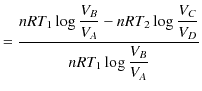 |
||
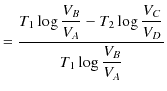 |
ここで,断熱変化 ![]() を考えると,
を考えると,
が成立します.ただし,![]() は比熱比です.同様に,断熱変化
は比熱比です.同様に,断熱変化 ![]() を考えると,
を考えると,
が成立します.この2つの等式を辺々割ると,
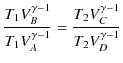 |
||
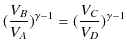 |
||
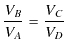 |
となります.最後の式を,![]() を表す上の式に代入すると,
を表す上の式に代入すると,
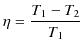
を得ます.故に,
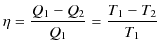 |
||
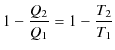 |
||
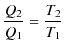 |
となります.したがって,理想気体の状態方程式の絶対温度と,熱力学的絶対温度は一致することが確かめられました.
熱力学的絶対温度の関係式を用いて,熱機関一般に成立する関係を導いてみましょう.熱力学的絶対温度の関係式より,
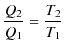 |
||
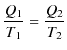 |
となります.ここで,放出される熱 ![]() は正ですが,これを負の
は正ですが,これを負の ![]() が吸収されると置き直します.そうすると,放出される熱は
が吸収されると置き直します.そうすると,放出される熱は ![]() になるので,
になるので,
という式が,カルノーサイクルについて成立します.(以降の議論では熱は吸収されるものとして統一し,放出されるときは負の熱を吸収しているとします.)さて,ある熱機関(可逆機関または不可逆機関)が絶対温度 ![]() の高熱源から熱
の高熱源から熱 ![]() をもらい,絶対温度
をもらい,絶対温度 ![]() の低熱源から熱
の低熱源から熱
![]() をもらっているとき,(つまり,低熱源には正の熱を放出しています.)この熱機関の熱効率
をもらっているとき,(つまり,低熱源には正の熱を放出しています.)この熱機関の熱効率 ![]() は,次式で表されます.
は,次式で表されます.
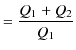 |
||
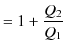 |
一方,可逆機関であるカルノーサイクルの熱効率 ![]() は次式でした.
は次式でした.
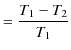 |
||
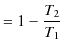 |
ここで,カルノーの定理より,
ですので,(等号は可逆変化に対して,不等号は不可逆変化に対して,それぞれ成立します.)
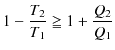 |
||
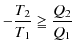 |
||
となります.よって,
となります.(3.2)式をクラウジウスの不等式といいます.(等号は可逆変化に対して,不等号は不可逆変化に対して,それぞれ成立します.)
次に,この関係を熱源が複数ある場合について拡張してみましょう.ただし,熱は熱機関に吸収されていると仮定し,放出される場合はそれが負の値をとるものとします.状況は下図の通りです.
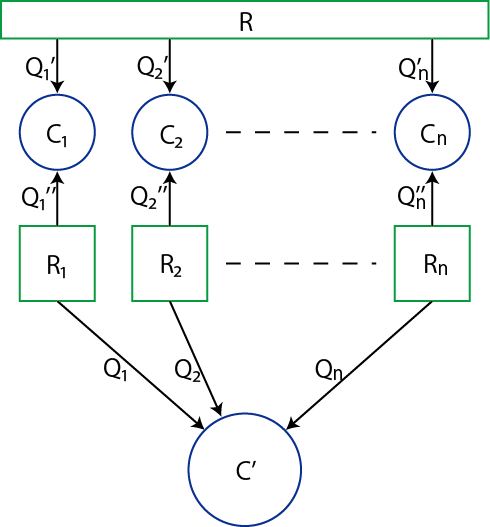
Figure3.3: クラウジウスの不等式1
![]() (絶対温度
(絶対温度 ![]() ),
),![]() (絶対温度
(絶対温度 ![]() ),
),![]() (絶対温度
(絶対温度 ![]() ),…,
),…,![]() (絶対温度
(絶対温度 ![]() )は熱源です.ただし,どれが高熱源で,どれが低熱源であるとは決めていません.
)は熱源です.ただし,どれが高熱源で,どれが低熱源であるとは決めていません.![]() は体系のサイクルで,可逆または不可逆であり,
は体系のサイクルで,可逆または不可逆であり,
![]() から熱
から熱
![]() を吸収すると仮定します.(吸収のとき熱は正,放出のとき熱は負と約束していました.)また,
を吸収すると仮定します.(吸収のとき熱は正,放出のとき熱は負と約束していました.)また,
![]() はカルノーサイクルであり,図のように熱を吸収すると仮定します.(吸収のとき熱は正,放出のとき熱は負です.)このとき,(3.1)式を各カルノーサイクルに適用して,
はカルノーサイクルであり,図のように熱を吸収すると仮定します.(吸収のとき熱は正,放出のとき熱は負です.)このとき,(3.1)式を各カルノーサイクルに適用して,
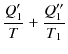 |
||
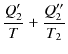 |
||
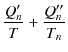 |
を得ます.これらの式を辺々足し上げると,
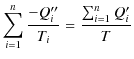
となります.ここで,すべてのサイクルが1サイクルだけ完了した時点で(つまり,
![]() が元に戻ったとき.),熱源
が元に戻ったとき.),熱源
![]() が元に戻るように
が元に戻るように
![]() を選ぶことができます.この場合,
を選ぶことができます.この場合,
の関係が成立します.したがって,上の式は,
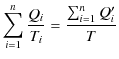
となります.また,![]() は外に仕事,
は外に仕事,
を行い,
![]() はそれぞれ外に仕事,
はそれぞれ外に仕事,
をします.故に,系全体で外にする仕事は,
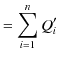 |
です.結局,全てのサイクルが1サイクルだけ完了した時点で,系全体は熱源 ![]() から,熱,
から,熱,
を吸収し,それを全部仕事に変えたことになります.これは,明らかに熱力学第二法則のトムソンの原理に反します.したがって,
としなければなりません.(不等号の場合,外から仕事をされて,それを全部熱源 ![]() に放出することになります.)もしもサイクル
に放出することになります.)もしもサイクル ![]() が可逆機関であれば,
が可逆機関であれば,
![]() は可逆なので系全体が可逆になり,上の操作を全て逆にすることができます.そのとき,
は可逆なので系全体が可逆になり,上の操作を全て逆にすることができます.そのとき,
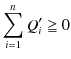
が成立しますが,これが(3.3)式と両立するためには,
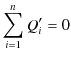
であり,この式が,![]() が可逆であること,つまり,系全体が可逆であることと等価になります.したがって,不等号が成立することと,
が可逆であること,つまり,系全体が可逆であることと等価になります.したがって,不等号が成立することと,![]() が不可逆であること,つまり,系全体が不可逆であることと等価になります.以上の議論により,
が不可逆であること,つまり,系全体が不可逆であることと等価になります.以上の議論により,
が成立します.(3.4)式もクラウジウスの不等式といいます.ここで,等号の場合は可逆変化,不等号の場合は不可逆変化です.また,(3.4)式で ![]() とおけば,当然(3.2)式になります.
とおけば,当然(3.2)式になります.
(3.4)式をさらに拡張して,![]() 個の熱源の代わりに連続的に絶対温度が変わる熱源を用意しましょう.系全体の1サイクルを下図のような閉曲線で表し,微小区間に分割します.
個の熱源の代わりに連続的に絶対温度が変わる熱源を用意しましょう.系全体の1サイクルを下図のような閉曲線で表し,微小区間に分割します.
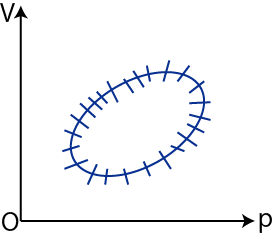
Figure3.4: クラウジウスの不等式2
各微小区間で系全体が吸収する熱を ![]() とします.ダッシュを付けたのは不完全微分であることを示すためです.また,その微小区間での絶対温度を
とします.ダッシュを付けたのは不完全微分であることを示すためです.また,その微小区間での絶対温度を ![]() とします.ここで,この絶対温度は系全体のものではなく,熱源の絶対温度であることに注意しましょう.微小区間を無限小にすると,(3.4)式の和は積分になり,次式が成立します.
とします.ここで,この絶対温度は系全体のものではなく,熱源の絶対温度であることに注意しましょう.微小区間を無限小にすると,(3.4)式の和は積分になり,次式が成立します.
(3.5)式もクラウジウスの不等式といいます.等号の場合は可逆変化,不等号の場合は不可逆変化です.積分記号に丸を付けたのは,サイクルが閉じていることを表すためです.
下図のような ![]() グラフにおける状態変化を考えます.ただし,全て可逆的準静変化であるとします.
グラフにおける状態変化を考えます.ただし,全て可逆的準静変化であるとします.
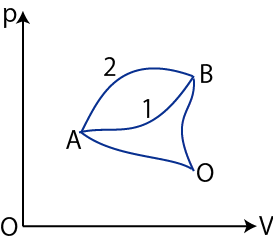
Figure3.5: エントロピー
このとき,
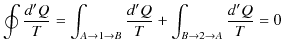
ここで,変化を逆にすると,熱の吸収と放出が逆になるので,
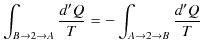
となります.したがって,
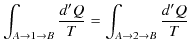
が成立します.つまり,この積分の量は途中の経路によらず,状態 ![]() と状態
と状態 ![]() だけで決まります.そこで,ある基準
だけで決まります.そこで,ある基準 ![]() をとり,次の積分で表される量を定義します.
をとり,次の積分で表される量を定義します.
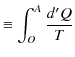 |
||
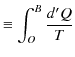 |
![]() は状態だけで決定されるので状態量です.また,基準
は状態だけで決定されるので状態量です.また,基準 ![]() の取り方による不定性があります.このとき,
の取り方による不定性があります.このとき,
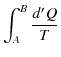 |
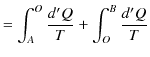 |
|
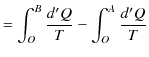 |
となり,
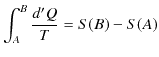
が成立します.ここで,状態量 ![]() をエントロピーといいます.エントロピーの微分は,
をエントロピーといいます.エントロピーの微分は,
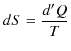
で与えられます.![]() が状態量なので,
が状態量なので,![]() は完全微分です.この式を書き直すと,
は完全微分です.この式を書き直すと,
なので,熱力学第1法則,
に代入すると,
が成立します.ここで,![]() の理想気体のエントロピーを求めてみましょう.定積モル比熱を
の理想気体のエントロピーを求めてみましょう.定積モル比熱を
![]() として,
として,
が成り立つので,(3.6)式に代入すると,
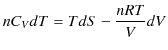 |
||
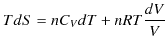 |
||
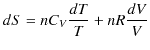 |
||
となります.最後の式が理想気体のエントロピーを表す式になります.
状態 ![]() から状態
から状態 ![]() へ不可逆変化で移り,状態
へ不可逆変化で移り,状態 ![]() から状態
から状態 ![]() へ可逆変化で戻る閉じた状態変化を考えましょう.クラウジウスの不等式より,次のように計算されます.ただし,式の中にあるRevは可逆変化を示し,Irrevは不可逆変化を表すものとします.
へ可逆変化で戻る閉じた状態変化を考えましょう.クラウジウスの不等式より,次のように計算されます.ただし,式の中にあるRevは可逆変化を示し,Irrevは不可逆変化を表すものとします.
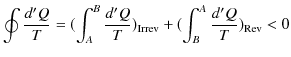 |
||
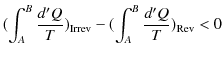 |
||
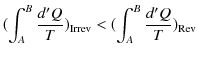 |
||
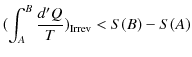 |
ここで,不可逆変化が入っているので,等号は成立せず,不等号のみ成立します.(全て可逆変化の場合には等号が成立します.)微小変化に対しては,
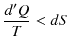
となります.ここで,断熱変化の場合を考えると,![]() は
は ![]() です.したがって,一般に,断熱変化
です.したがって,一般に,断熱変化 ![]() に対して,
に対して,
が成立します.微小変化に対しては,
です.言い換えると,
法則3.3(熱力学第二法則3(エントロピー増大の法則)) "不可逆断熱変化では,エントロピーは必ず増大します."
ということが言えます.これをエントロピー増大の法則といい,熱力学第二法則の3つ目の表現でした.なお,可逆断熱変化ではエントロピーは変化しません.
統計力学の立場では,エントロピーとは乱雑さを与えるものであり,それが増大するように不可逆変化が起こるのです.
エントロピーについて,次の熱力学第三法則(ネルンスト-プランクの定理)が成立します.
法則3.4(熱力学第三法則(ネルンスト-プランクの定理)) "化学的に一様で有限な密度をもつ物体のエントロピーは,温度が絶対零度に近づくにしたがい,圧力,密度,相によらず一定値に近づきます."
この一定値をゼロにとり,エントロピーの絶対値を定めることができます.
熱力学の立場では,熱力学第三法則は,第0,第一,第二法則と同様に経験法則です.しかし,統計力学の立場では,第三法則は理論的に導かれる定理です.