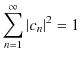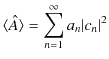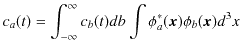J Simplicity 波動力学の展開

Chapter9 波動力学の展開

9.1 離散固有関数と離散固有値

波動力学においては，多くの微分方程式は固有値方程式で表されます．跳び跳びの性質をもつ離散固有関数と離散固有値について調べましょう．一般に離散固有値方程式は，

$\displaystyle \hat{A}\phi_{n}(\bm{x})=a_{n}\phi_{n}(\bm{x})\,(n=1,2,\cdots)$

という形式をしています． $\hat{A}$ は線形エルミート演算子， $\phi_{n}(\bm{x})$ は離散固有関数， $a_{n}$ は離散固有値です．離散固有関数と離散固有値は，それぞれ添え字の自然数で区別しています．（は跳び跳びに変化しますが，一般に無限個あります．）（時間に依存しないシュレディンガー方程式の解について，波動関数 $\phi(\bm{x})$ が離散固有関数になり，固有値が離散固有値となる量子状態を一般に束縛状態といいます．）これから述べることは，時間に依存しないシュレディンガー方程式の離散エネルギー固有関数と離散エネルギー固有値だけに限らず，線形エルミート演算子の離散固有関数と離散固有値一般について言えることです．

　エルミート演算子 $\hat{A}$ について，

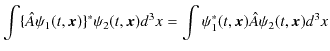
$\displaystyle \int\{\hat{A}\psi_{1}(t,\bm{x})\}^{*}\psi_{2}(t,\bm{x})d^{3}x=\int\psi_{1}^{*}(t,\bm{x})\hat{A}\psi_{2}(t,\bm{x})d^{3}x$

の関係が成立します．ただし，3次元の積分記号は，

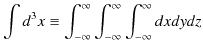
$\displaystyle \int d^{3}x\equiv\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}dxdydz$

と約束していました．粒子は全空間で存在する確率がありますので，積分範囲はこのようにとります．ここで，時間と位置の関数 $\psi(t,\bm{x})$ において，時間を固定し，位置のみの関数 $\phi(\bm{x})$ を特別な場合としてとることができます．そこで， $\psi_{1}(t,\bm{x})\to\phi_{n}(\bm{x}),\psi_{2}(t,\bm{x})\to\phi_{m}(\bm{x})$ とおきます．

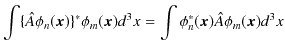	$\displaystyle \int\{\hat{A}\phi_{n}(\bm{x})\}^{}\phi_{m}(\bm{x})d^{3}x=\int\phi_{n}^{}(\bm{x})\hat{A}\phi_{m}(\bm{x})d^{3}x$
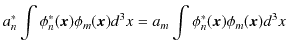$% latex2html id marker 2377 $\displaystyle \therefore$$	$\displaystyle a_{n}^{}\int\phi_{n}^{}(\bm{x})\phi_{m}(\bm{x})d^{3}x=a_{m}\int\phi_{n}^{*}(\bm{x})\phi_{m}(\bm{x})d^{3}x$

エルミート演算子の固有値は実数なので，

$\displaystyle a_{n}^{*}=a_{n}$

です．よって，

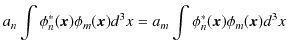	$\displaystyle a_{n}\int\phi_{n}^{}(\bm{x})\phi_{m}(\bm{x})d^{3}x=a_{m}\int\phi_{n}^{}(\bm{x})\phi_{m}(\bm{x})d^{3}x$
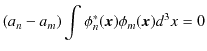$% latex2html id marker 2382 $\displaystyle \therefore$$	$\displaystyle (a_{n}-a_{m})\int\phi_{n}^{*}(\bm{x})\phi_{m}(\bm{x})d^{3}x=0$

となります．異なる固有関数についての固有値が等しくないとき，つまり，

$\displaystyle a_{n}\neq a_{m}$

の場合，

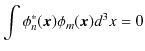
$\displaystyle \int\phi_{n}^{*}(\bm{x})\phi_{m}(\bm{x})d^{3}x=0$

の関係が成立します．このとき，固有関数は直交するといいます．すなわち，

定理9.1 "エルミート演算子の異なる離散固有値に属する２つの離散固有関数は直交します．"

という定理が証明されました．また，全空間での1個の粒子が観測される確率がであるという，時間に依存しない波動関数 $\phi(\bm{x})$ についての規格化条件，

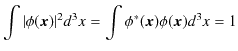
$\displaystyle \int\vert\phi(\bm{x})\vert^{2}d^{3}x=\int\phi^{*}(\bm{x})\phi(\bm{x})d^{3}x=1$

において， $\phi(\bm{x})$ としてある番目の離散固有関数をとります．このとき，

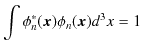
$\displaystyle \int\phi_{n}^{*}(\bm{x})\phi_{n}(\bm{x})d^{3}x=1$

の関係が成立します．

　さて，ある1つの固有値に対して，固有関数が1個しかないとき，固有関数は縮退していないといいます．一方，ある1つの固有値に対して，固有関数が個（ $g\geqq2$ ）存在するとき，固有関数は重に縮退しているといいます．上の議論は固有関数が縮退していないことを前提としていましたが，縮退している場合には，次のグラム-シュミットの直交化法を使います．いま，

$\displaystyle \phi_{1}(\bm{x}),\phi_{2}(\bm{x}),\cdots,\phi_{g}(\bm{x})$

が同じ固有値をもつ重に縮退した固有関数とします．まず，

$\displaystyle \phi'_{1}(\bm{x})=\alpha\phi_{1}(\bm{x})$

とおき， $\phi'_{1}(\bm{x})$ についての規格化条件，

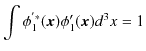
$\displaystyle \int\phi_{1}^{'*}(\bm{x})\phi'_{1}(\bm{x})d^{3}x=1$

を満たすように，定数 $\alpha$ を決めます．次に，

$\displaystyle \phi'_{2}(\bm{x})=\beta_{1}\phi'_{1}(\bm{x})+\beta_{2}\phi_{2}(\bm{x})$

とおき， $\phi'_{1}(\bm{x})$ と $\phi'_{2}(\bm{x})$ の直交条件，

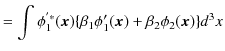$\displaystyle \int\phi_{1}^{'*}(\bm{x})\phi'_{2}(\bm{x})d^{3}x$	$\displaystyle =\int\phi_{1}^{'*}(\bm{x})\{\beta_{1}\phi'_{1}(\bm{x})+\beta_{2}\phi_{2}(\bm{x})\}d^{3}x$
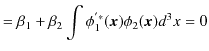	$\displaystyle =\beta_{1}+\beta_{2}\int\phi_{1}^{'*}(\bm{x})\phi_{2}(\bm{x})d^{3}x=0$

と， $\phi'_{2}(\bm{x})$ の規格化条件，

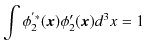
$\displaystyle \int\phi_{2}^{'*}(\bm{x})\phi'_{2}(\bm{x})d^{3}x=1$

より， $\beta_{1},\beta_{2}$ を決定し， $\phi'_{2}(\bm{x})$ を求めます．さらに，

$\displaystyle \phi'_{3}(\bm{x})=\gamma_{1}\phi'_{1}(\bm{x})+\gamma_{2}\phi'_{2}(\bm{x})+\gamma_{3}\phi_{3}(\bm{x})$

とおき，同様な議論をします．以下，その繰り返しです．最終的に得られた規格化条件と直交条件を満たす複数の固有関数のダッシュをとります．このように，縮退がある場合も必ず直交化することができます.

　規格化条件と直交条件をまとめて表した条件を規格直交条件といい，次の条件式で表すことができます．

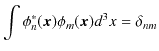
$\displaystyle \int\phi_{n}^{*}(\bm{x})\phi_{m}(\bm{x})d^{3}x=\delta_{nm}$

このときの $\phi(\bm{x})$ の集合全体を規格直交系といいます．ただし，右辺の記号はクロネッカーの $\delta$ （デルタ）といい，

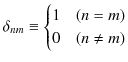
$\displaystyle \delta_{nm}\equiv\begin{cases} 1 & (n=m)\\ 0 & (n\neq m) \end{cases}$

で定義されます．言い直すと，離散固有関数について，

　"離散固有値をもつエルミート演算子の離散固有関数の全体は，規格直交系を形成しています．"

という重要な性質があります．

　時間に依存する波動関数 $\psi(t,\bm{x})$ についての重ね合わせの原理を，時間に依存しない波動関数 $\phi(\bm{x})$ について適用した議論を思い出しましょう．（"量子状態（波動関数と確率振幅）" のChapterを参照して下さい．）そのとき，

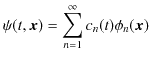
$\displaystyle \psi(t,\bm{x})=\sum_{n=1}^{\infty}c_{n}(t)\phi_{n}(\bm{x})$

の関係式が成立しました．ここで， $\phi(\bm{x})$ として規格直交系を形成する離散固有関数の集合全体 $\{\phi_{1}(\bm{x}),\phi_{2}(\bm{x}),\cdots\}$ を採った場合，任意の $\psi(t,\bm{x})$ は，上記のように展開して表せます．（一般に，固有関数は無限個あるので，添え字はから無限大まで和をとります．以下，断りがなければ同様とします．）このとき，規格直交系 $\{\phi_{1}(\bm{x}),\phi_{2}(\bm{x}),\cdots\}$ を完全系であるといいます．完全系を成し任意の $\psi(t,\bm{x})$ を展開して表せるということと，規格直交系の条件を満たすという意味で， $\{\phi_{1}(\bm{x}),\phi_{2}(\bm{x}),\cdots\}$ を基底といいます．ここで，展開係数は，

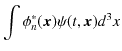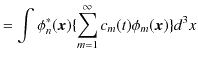$\displaystyle \int\phi_{n}^{*}(\bm{x})\psi(t,\bm{x})d^{3}x$	$\displaystyle =\int\phi_{n}^{*}(\bm{x})\{\sum_{m=1}^{\infty}c_{m}(t)\phi_{m}(\bm{x})\}d^{3}x$
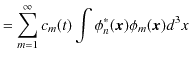	$\displaystyle =\sum_{m=1}^{\infty}c_{m}(t)\int\phi_{n}^{*}(\bm{x})\phi_{m}(\bm{x})d^{3}x$
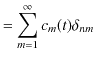	$\displaystyle =\sum_{m=1}^{\infty}c_{m}(t)\delta_{nm}$
	$\displaystyle =c_{1}(t)\delta_{n1}+c_{2}(t)\delta_{n2}+\cdots+c_{n-1}(t)\delta_{n,n-1}+c_{n}(t)\delta_{nn}+c_{n+1}(t)\delta_{n,n+1}+\cdots$
	$\displaystyle =c_{1}(t)\cdot0+c_{2}(t)\cdot0+\cdots+c_{n-1}(t)\cdot0+c_{n}(t)\cdot1+c_{n+1}(t)\cdot0+\cdots$
	$\displaystyle =c_{n}(t)$

ですから，故に，

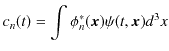
$\displaystyle c_{n}(t)=\int\phi_{n}^{*}(\bm{x})\psi(t,\bm{x})d^{3}x$

より求められます．また，波動関数 $\psi(t,\bm{x})$ に対する規格化条件より，

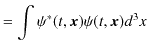$\displaystyle 1$	$\displaystyle =\int\psi^{*}(t,\bm{x})\psi(t,\bm{x})d^{3}x$
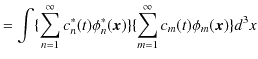	$\displaystyle =\int\{\sum_{n=1}^{\infty}c_{n}^{}(t)\phi_{n}^{}(\bm{x})\}\{\sum_{m=1}^{\infty}c_{m}(t)\phi_{m}(\bm{x})\}d^{3}x$
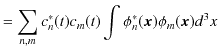	$\displaystyle =\sum_{n,m}c_{n}^{}(t)c_{m}(t)\int\phi_{n}^{}(\bm{x})\phi_{m}(\bm{x})d^{3}x$
	$\displaystyle =\sum_{n,m}c_{n}^{*}(t)c_{m}(t)\delta_{nm}$
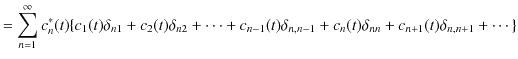	$\displaystyle =\sum_{n=1}^{\infty}c_{n}^{*}(t)\{c_{1}(t)\delta_{n1}+c_{2}(t)\de... ...+c_{n-1}(t)\delta_{n,n-1}+c_{n}(t)\delta_{nn}+c_{n+1}(t)\delta_{n,n+1}+\cdots\}$
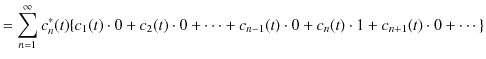	$\displaystyle =\sum_{n=1}^{\infty}c_{n}^{*}(t)\{c_{1}(t)\cdot0+c_{2}(t)\cdot0+\cdots+c_{n-1}(t)\cdot0+c_{n}(t)\cdot1+c_{n+1}(t)\cdot0+\cdots\}$
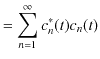	$\displaystyle =\sum_{n=1}^{\infty}c_{n}^{*}(t)c_{n}(t)$
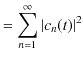	$\displaystyle =\sum_{n=1}^{\infty}\vert c_{n}(t)\vert^{2}$

ですから，故に，

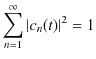
$\displaystyle \sum_{n=1}^{\infty}\vert c_{n}(t)\vert^{2}=1$

となります．ここで，

$\displaystyle c_{n}(t)\equiv c_{n}e^{-i\omega_{n}t}$

という関係がありました．（"量子状態（波動関数と確率振幅）" のChapterを参照して下さい．）したがって，

$\displaystyle \vert c_{n}(t)\vert^{2}$	$\displaystyle =c_{n}^{*}(t)c_{n}(t)$
	$\displaystyle =c_{n}^{*}e^{i\omega_{n}t}\cdot c_{n}e^{-i\omega_{n}t}$
	$\displaystyle =\vert c_{n}\vert^{2}$

より，

$\displaystyle \sum_{n=1}^{\infty}\vert c_{n}\vert^{2}=1$

(9.1)

の関係式が成立します．また，物理量の期待値は，

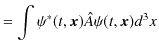$\displaystyle \langle\hat{A}\rangle$	$\displaystyle =\int\psi^{*}(t,\bm{x})\hat{A}\psi(t,\bm{x})d^{3}x$
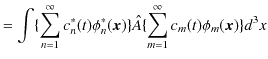	$\displaystyle =\int\{\sum_{n=1}^{\infty}c_{n}^{}(t)\phi_{n}^{}(\bm{x})\}\hat{A}\{\sum_{m=1}^{\infty}c_{m}(t)\phi_{m}(\bm{x})\}d^{3}x$
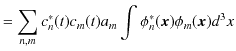	$\displaystyle =\sum_{n,m}c_{n}^{}(t)c_{m}(t)a_{m}\int\phi_{n}^{}(\bm{x})\phi_{m}(\bm{x})d^{3}x$
	$\displaystyle =\sum_{n,m}c_{n}^{*}(t)c_{m}(t)a_{m}\delta_{nm}$
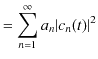	$\displaystyle =\sum_{n=1}^{\infty}a_{n}\vert c_{n}(t)\vert^{2}$
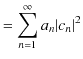	$\displaystyle =\sum_{n=1}^{\infty}a_{n}\vert c_{n}\vert^{2}$

より，

$\displaystyle \langle\hat{A}\rangle=\sum_{n=1}^{\infty}a_{n}\vert c_{n}\vert^{2}$

(9.2)

と表せます．つまり，期待値は固有値 $a_{n}$ に $\vert c_{n}\vert^{2}$ をかけて，全てのについての和をとったものになります．この(9.2)式と，その上にある(9.1)式より， $\vert c_{n}\vert^{2}$ は状態が $\phi_{n}(\bm{x})$ になり，固有値 $a_{n}$ を測定する確率であると解釈することができます．ここで，"オブザーバブル（線形エルミート演算子と期待値・固有値）" のChapterも参考にして，離散固有関数と離散固有値について，まとめておきます．

　"離散固有値問題で設定された物理系で，理想実験し観測すると，固有値の中のいずれか（例えば $a_{n}$ ．）を測定することになります．（理論値である固有値が，量子力学的理想測定値であるということになります．）一旦，固有値 $a_{n}$ を測定すると，量子状態を表す波動関数はその固有値 $a_{n}$ の固有状態 $\phi_{n}(\bm{x})$ に量子飛躍します．

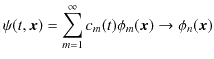
$\displaystyle \psi(t,\bm{x})=\sum_{m=1}^{\infty}c_{m}(t)\phi_{m}(\bm{x})\to\phi_{n}(\bm{x})$

逆に，固有状態 $\phi_{n}(\bm{x})$ において測定すると，測定値は必ず固有値 $a_{n}$ になります．量子飛躍は不連続的に起こり，その前後で因果関係はありません．ただし，波動関数が $\phi_{n}(\bm{x})$ になり，測定値に一致する固有値が $a_{n}$ になる確率は，展開係数の絶対値の２乗 $\vert c_{n}\vert^{2}$ で与えられます．"

9.2 数学的準備（δ関数）

次に連続固有関数と連続固有値を取り扱いますが，その前に数学的準備をしておきましょう．離散固有関数を取り扱う際，クロネッカーのデルタという量を頻繁に使いました．定義を再掲すると，

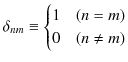
$\displaystyle \delta_{nm}\equiv\begin{cases} 1 & (n=m)\\ 0 & (n\neq m) \end{cases}$

でした．連続固有関数の場合，それに代わってディラックのδ関数という関数を導入します．定義は，

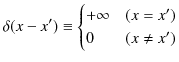
$\displaystyle \delta(x-x')\equiv\begin{cases} +\infty&(x=x')\\ 0&(x\neq x') \end{cases}$

と，

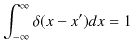
$\displaystyle \int_{-\infty}^{\infty}\delta(x-x')dx=1$

からなります．δ関数は直観的には，の点で無限大になる針のように尖った関数で， $x\neq x'$ では 0 の値をとります．そして，その面積は $-\infty$ から $+\infty$ まで積分してみると丁度になります．このような関数は普通の関数ではなく超関数と呼ばれるものです．δ関数の満たす公式を幾つか導いておきます．任意の関数に対して，

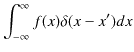
$\displaystyle \int_{-\infty}^{\infty}f(x)\delta(x-x')dx$

という積分を考えます． $x\neq x'$ で， $\delta(x-x')=0$ なので， $x\neq x'$ でのの値は上の積分には寄与しません．したがって，

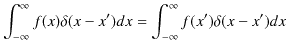
$\displaystyle \int_{-\infty}^{\infty}f(x)\delta(x-x')dx=\int_{-\infty}^{\infty}f(x')\delta(x-x')dx$

となります．ここで，は定数なので，積分の外に出すことができます．

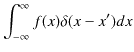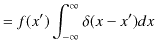$\displaystyle \int_{-\infty}^{\infty}f(x)\delta(x-x')dx$	$\displaystyle =f(x')\int_{-\infty}^{\infty}\delta(x-x')dx$
	$\displaystyle =f(x')\cdot1$

故に，

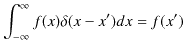
$\displaystyle \int_{-\infty}^{\infty}f(x)\delta(x-x')dx=f(x')$

が成立します．離散固有関数においてクロネッカーのデルタが使われたように，連続固有関数において，この関係式はよく使われます．次に，δ関数が偶関数であることを証明します．

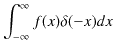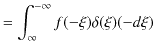$\displaystyle \int_{-\infty}^{\infty}f(x)\delta(-x)dx$	$\displaystyle =\int_{\infty}^{-\infty}f(-\xi)\delta(\xi)(-d\xi)$
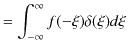	$\displaystyle =\int_{-\infty}^{\infty}f(-\xi)\delta(\xi)d\xi$
	$\displaystyle =f(-0)$
	$\displaystyle =f(0)$
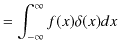	$\displaystyle =\int_{-\infty}^{\infty}f(x)\delta(x)dx$

故に，

$\displaystyle \delta(x)=\delta(-x)$

が成立します．また，

$\displaystyle x\delta(x)=0$

が成立します．証明は次の通りです．を任意の関数として，

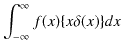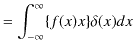$\displaystyle \int_{-\infty}^{\infty}f(x)\{x\delta(x)\}dx$	$\displaystyle =\int_{-\infty}^{\infty}\{f(x)x\}\delta(x)dx$
	$\displaystyle =f(0)\cdot0$
	$\displaystyle =0$

となります．故に，

$\displaystyle x\delta(x)=0$

が証明されました．（は任意の関数です．）最後に，

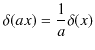
$\displaystyle \delta(ax)=\dfrac{1}{a}\delta(x)$

を導きます．

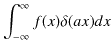$\displaystyle \int_{-\infty}^{\infty}f(x)\delta(ax)dx$	$\displaystyle =\int_{-\infty}^{\infty}f(\dfrac{\xi}{a})\delta(\xi)\dfrac{d\xi}{a}$
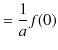	$\displaystyle =\dfrac{1}{a}f(0)$
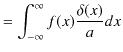	$\displaystyle =\int_{-\infty}^{\infty}f(x)\dfrac{\delta(x)}{a}dx$

よって，

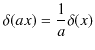
$\displaystyle \delta(ax)=\dfrac{1}{a}\delta(x)$

です．（以上，証明終．）

　ここで，一般に関数のフーリエ変換，

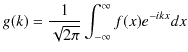
$\displaystyle g(k)=\dfrac{1}{\sqrt{2\pi}}\int_{-\infty}^{\infty}f(x)e^{-ikx}dx$

とフーリエ逆変換，

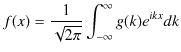
$\displaystyle f(x)=\dfrac{1}{\sqrt{2\pi}}\int_{-\infty}^{\infty}g(k)e^{ikx}dk$

を考えます．として，δ関数 $\delta(x)$ を代入すると，フーリエ変換より，

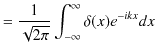$\displaystyle g(k)$	$\displaystyle =\dfrac{1}{\sqrt{2\pi}}\int_{-\infty}^{\infty}\delta(x)e^{-ikx}dx$
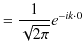	$\displaystyle =\dfrac{1}{\sqrt{2\pi}}e^{-ik\cdot0}$
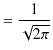	$\displaystyle =\dfrac{1}{\sqrt{2\pi}}$

となります．さらに，フーリエ逆変換より，

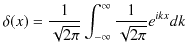	$\displaystyle \delta(x)=\dfrac{1}{\sqrt{2\pi}}\int_{-\infty}^{\infty}\dfrac{1}{\sqrt{2\pi}}e^{ikx}dk$
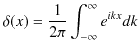$% latex2html id marker 2625 $\displaystyle \therefore$$	$\displaystyle \delta(x)=\dfrac{1}{2\pi}\int_{-\infty}^{\infty}e^{ikx}dk$

と表せます．このδ関数の表式はよく使われます．また，３次元のδ関数を次の式で定義しておきます．

$\displaystyle \delta^{3}(\bm{x}-\bm{x}')\equiv\delta(x-x')\delta(y-y')\delta(z-z')$

上の複素数の指数関数を使った表式も３次元で表しておきます．

$\displaystyle \delta^{3}(\bm{x})$	$\displaystyle =\delta(x)\delta(y)\delta(z)$
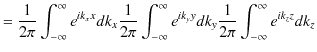	$\displaystyle =\dfrac{1}{2\pi}\int_{-\infty}^{\infty}e^{ik_{x}x}dk_{x}\dfrac{1}... ...\infty}e^{ik_{y}y}dk_{y}\dfrac{1}{2\pi}\int_{-\infty}^{\infty}e^{ik_{z}z}dk_{z}$
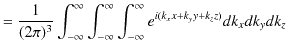	$\displaystyle =\dfrac{1}{(2\pi)^{3}}\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}e^{i(k_{x}x+k_{y}y+k_{z}z)}dk_{x}dk_{y}dk_{z}$

ですから，

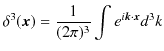
$\displaystyle \delta^{3}(\bm{x})=\dfrac{1}{(2\pi)^{3}}\int e^{i\bm{k}\cdot\bm{x}}d^{3}k$

が成立します．（ただし，3次元の積分記号は，

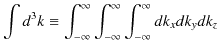
$\displaystyle \int d^{3}k\equiv\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}dk_{x}dk_{y}dk_{z}$

と約束します．）この式を使えば，3次元フーリエ変換が，

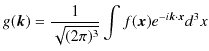
$\displaystyle g(\bm{k})=\dfrac{1}{\sqrt{(2\pi)^{3}}}\int f(\bm{x})e^{-i\bm{k}\cdot\bm{x}}d^{3}x$

であり，3次元フーリエ逆変換が，

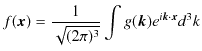
$\displaystyle f(\bm{x})=\dfrac{1}{\sqrt{(2\pi)^{3}}}\int g(\bm{k})e^{i\bm{k}\cdot\bm{x}}d^{3}k$

であることが，次のように確認されます．

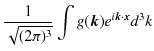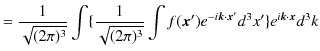$\displaystyle \dfrac{1}{\sqrt{(2\pi)^{3}}}\int g(\bm{k})e^{i\bm{k}\cdot\bm{x}}d^{3}k$	$\displaystyle =\dfrac{1}{\sqrt{(2\pi)^{3}}}\int\{\dfrac{1}{\sqrt{(2\pi)^{3}}}\int f(\bm{x}')e^{-i\bm{k}\cdot\bm{x}'}d^{3}x'\}e^{i\bm{k}\cdot\bm{x}}d^{3}k$
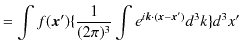	$\displaystyle =\int f(\bm{x}')\{\dfrac{1}{(2\pi)^{3}}\int e^{i\bm{k}\cdot(\bm{x}-\bm{x}')}d^{3}k\}d^{3}x'$
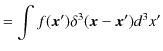	$\displaystyle =\int f(\bm{x}')\delta^{3}(\bm{x}-\bm{x}')d^{3}x'$
	$\displaystyle =f(\bm{x})$

9.3 連続固有関数と連続固有値

連続した性質をもつ連続固有関数と連続固有値について調べましょう．一般に連続固有値方程式は，

$\displaystyle \hat{A}\phi_{a}(\bm{x})=a\phi_{a}(\bm{x})$

という形式をしています． $\hat{A}$ は線形エルミート演算子， $\phi_{a}(\bm{x})$ は連続固有関数，は連続固有値です．連続固有関数と連続固有値は，で区別しています．（は連続的に変化します．無限個の連続固有関数と無限個の連続固有値があります．）（時間に依存しないシュレディンガー方程式の解について，波動関数 $\phi(\bm{x})$ が連続固有関数になり，固有値が連続固有値となる量子状態を一般に散乱状態といいます．）以下の記述については，時間に依存しないシュレディンガー方程式の連続エネルギー固有関数と連続エネルギー固有値だけに限らず，線形エルミート演算子の連続固有関数と連続固有値一般について言えることです．

　離散固有関数の場合と同じように，波動関数 $\psi(t,\bm{x})$ を連続固有関数 $\phi(\bm{x})$ で展開することができます．ただし，離散固有関数の場合は無限級数の和でしたが，連続固有関数の場合は積分になります．

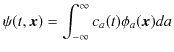
$\displaystyle \psi(t,\bm{x})=\int_{-\infty}^{\infty}c_{a}(t)\phi_{a}(\bm{x})da$

ここで，離散固有関数の場合と同様に， $c_{a}(t)$ は確率に関する展開係数で，

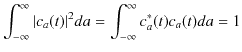
$\displaystyle \int_{-\infty}^{\infty}\vert c_{a}(t)\vert^{2}da=\int_{-\infty}^{\infty}c_{a}^{*}(t)c_{a}(t)da=1$

を満たします．離散固有関数の場合と同様に，

$\displaystyle \vert c_{a}(t)\vert^{2}$	$\displaystyle =c_{a}^{*}(t)c_{a}(t)$
	$\displaystyle =c_{a}^{*}e^{i\omega_{a}t}\cdot c_{a}e^{-i\omega_{a}t}$
	$\displaystyle =\vert c_{a}\vert^{2}$

となります． $\vert c_{a}(t)\vert^{2}da=\vert c_{a}\vert^{2}da$ は状態が $\phi_{a}(\bm{x})$ になり，固有値を測定する確率であると解釈することができます．また， $\psi(t,\bm{x})$ は規格化条件を満たします．

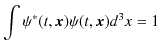
$\displaystyle \int\psi^{*}(t,\bm{x})\psi(t,\bm{x})d^{3}x=1$

この式に，上の $\psi(t,\bm{x})$ を展開した式を代入して計算します．

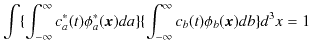	$\displaystyle \int\{\int_{-\infty}^{\infty}c_{a}^{}(t)\phi_{a}^{}(\bm{x})da\}\{\int_{-\infty}^{\infty}c_{b}(t)\phi_{b}(\bm{x})db\}d^{3}x=1$
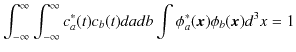$% latex2html id marker 2688 $\displaystyle \therefore$$	$\displaystyle \int_{-\infty}^{\infty}\int_{-\infty}^{\infty}c_{a}^{}(t)c_{b}(t)dadb\int\phi_{a}^{}(\bm{x})\phi_{b}(\bm{x})d^{3}x=1$

最後の式と，上述した，

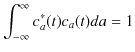
$\displaystyle \int_{-\infty}^{\infty}c_{a}^{*}(t)c_{a}(t)da=1$

の式を比較して，

$\displaystyle c_{a}(t)=\int_{-\infty}^{\infty}c_{b}(t)db\int\phi_{a}^{*}(\bm{x})\phi_{b}(\bm{x})d^{3}x$

(9.3)

が得られます．このとき，δ関数の性質より，

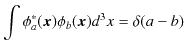
$\displaystyle \int\phi_{a}^{*}(\bm{x})\phi_{b}(\bm{x})d^{3}x=\delta(a-b)$

の関係式が成立します．この式を連続固有関数のδ関数規格直交条件といいます．（このとき，上の式を(9.3)式の右辺に代入して計算すると，

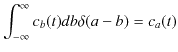
$\displaystyle \int_{-\infty}^{\infty}c_{b}(t)db\delta(a-b)=c_{a}(t)$

と確かめられます．）このSectionの最後に連続固有関数と連続固有値について，離散固有関数，離散固有値に対比させてまとめておきます．

　"連続固有値問題で設定された物理系で，理想実験し観測すると，固有値の中のいずれか（例えば．）を測定することになります．（理論値である固有値が，量子力学的理想測定値であるということになります．）一旦，固有値を測定すると，量子状態を表す波動関数はその固有値の固有状態 $\phi_{a}(\bm{x})$ に量子飛躍します．

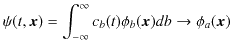
$\displaystyle \psi(t,\bm{x})=\int_{-\infty}^{\infty}c_{b}(t)\phi_{b}(\bm{x})db\to\phi_{a}(\bm{x})$

逆に，固有状態 $\phi_{a}(\bm{x})$ において測定すると，測定値は必ず固有値になります．量子飛躍は不連続的に起こり，その前後で因果関係はありません．状態が $\phi_{a}(\bm{x})$ になり，固有値を測定する確率は $\vert c_{a}\vert^{2}da$ で与えられます．"

9.4 表示

時間に依存しないシュレディンガー方程式の離散固有値方程式，

$\displaystyle \hat{H}(\bm{x},-i\hbar\bm{\nabla})\phi_{n}(\bm{x})=E_{n}\phi_{n}(\bm{x})\,(n=1,2,\cdots)$

を解くと，完全系，

$\displaystyle \{\phi_{1}(\bm{x}),\phi_{2}(\bm{x}),\cdots\}$

が得られ，これを基底に選び，任意の関数を展開することができます．

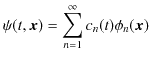
$\displaystyle \psi(t,\bm{x})=\sum_{n=1}^{\infty}c_{n}(t)\phi_{n}(\bm{x})$

また，時間に依存しないシュレディンガー方程式の連続固有値方程式，

$\displaystyle \hat{H}(\bm{x},-i\hbar\bm{\nabla})\phi_{E}(\bm{x})=E\phi_{E}(\bm{x})$

を解くと，完全系，

$\displaystyle \{\phi_{E}(\bm{x})\}$

が得られ，これを基底に選び，任意の関数を展開することができます．

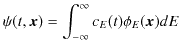
$\displaystyle \psi(t,\bm{x})=\int_{-\infty}^{\infty}c_{E}(t)\phi_{E}(\bm{x})dE$

このように時間に依存しないシュレディンガー方程式のエネルギー固有関数を基底として選び任意の関数を表すことを，エネルギー表示をとるといいます．

　表示の取り方，つまり基底の選択の方法として，他に位置表示と運動量表示というものが存在します．位置表示から考えましょう．位置演算子に対する固有値方程式はどのような形になるでしょうか？いままでの固有値方程式の形式で表現すると，位置演算子 $\hat{x}=x$ について，

$\displaystyle \hat{x}\phi_{x'}(x)=x'\phi_{x'}(x)$

となるでしょう．（１次元で考えました．は位置の変数，は，ある位置の定数です．）実は，この方程式を満たす固有関数はδ関数であることがわかっています．つまり，

$\displaystyle \hat{x}\delta(x-x')=x'\delta(x-x')$

が成立します．（連続固有値方程式になります．）証明は，左辺と右辺をそれぞれ積分すればできます．左辺を積分して，

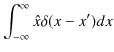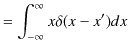$\displaystyle \int_{-\infty}^{\infty}\hat{x}\delta(x-x')dx$	$\displaystyle =\int_{-\infty}^{\infty}x\delta(x-x')dx$
	$\displaystyle =x'$

です．一方，右辺を積分して，

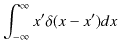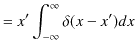$\displaystyle \int_{-\infty}^{\infty}x'\delta(x-x')dx$	$\displaystyle =x'\int_{-\infty}^{\infty}\delta(x-x')dx$
	$\displaystyle =x'$

です．（証明終．）改めて位置演算子の固有関数を，

$\displaystyle \phi_{x'}(x)=\delta(x-x')$

とおいて表しておきます．3次元に一般化すると，位置演算子の固有値方程式は次のようになります．

$\displaystyle \hat{\bm{x}}\delta^{3}(\bm{x}-\bm{x}')=\bm{x}'\delta^{3}(\bm{x}-\bm{x}')$

ただし，

$\displaystyle \delta^{3}(\bm{x}-\bm{x}')=\delta(x-x')\delta(y-y')\delta(z-z')$

です．このとき，位置演算子の固有関数は，

$\displaystyle \phi_{\bm{x}'}(\bm{x})=\delta^{3}(\bm{x}-\bm{x}')$

です．位置表示では， $\phi_{\bm{x}'}(\bm{x})=\delta^{3}(\bm{x}-\bm{x}')$ を基底にとり，任意の関数 $\psi(t,\bm{x})$ を展開します．

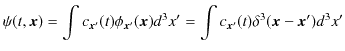
$\displaystyle \psi(t,\bm{x})=\int c_{\bm{x}'}(t)\phi_{\bm{x}'}(\bm{x})d^{3}x'=\int c_{\bm{x}'}(t)\delta^{3}(\bm{x}-\bm{x}')d^{3}x'$

また， $\phi_{\bm{x}'}(\bm{x})=\delta^{3}(\bm{x}-\bm{x}')$ は，次のδ関数規格直交条件を満たしています．

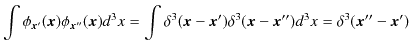
$\displaystyle \int\phi_{\bm{x}'}(\bm{x})\phi_{\bm{x}''}(\bm{x})d^{3}x=\int\delt... ...}(\bm{x}-\bm{x}')\delta^{3}(\bm{x}-\bm{x}'')d^{3}x=\delta^{3}(\bm{x}''-\bm{x}')$

導出は，δ関数の性質，

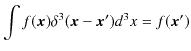
$\displaystyle \int f(\bm{x})\delta^{3}(\bm{x}-\bm{x}')d^{3}x=f(\bm{x}')$

により実行することができます．観測による量子飛躍についても考えておきます．"連続固有関数と連続固有値" のSectionを参考にして，全く同じ形式に揃えて記述すると，

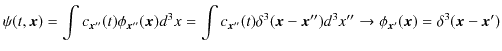
$\displaystyle \psi(t,\bm{x})=\int c_{\bm{x}''}(t)\phi_{\bm{x}''}(\bm{x})d^{3}x=... ...3}(\bm{x}-\bm{x}'')d^{3}x''\to\phi_{\bm{x}'}(\bm{x})=\delta^{3}(\bm{x}-\bm{x}')$

となります．この結果は，直観的に非常にわかりやすいものとなっています．すなわち，時間的に変動していて，空間的に広がっている波動関数が，観測した瞬間に，ある位置 $\bm{x}'$ に局在し，粒子として発見されることになります．このことは，"量子状態（波動関数と確率振幅）" のChapterでの観測による量子飛躍の表式，

$\displaystyle \psi(t,\bm{x})\to\phi_{\bm{x}'}$

と完全に一致します．つまり，矢印の右にある波動関数は，ある位置 $\bm{x}'$ に状態が局在することを示しているのですが，それが位置演算子の固有関数であるδ関数 $\delta^{3}(\bm{x}-\bm{x}')$ だったということが判明したのです．

$\displaystyle \psi(t,\bm{x})\to\phi_{\bm{x}'}=\delta^{3}(\bm{x}-\bm{x}')$

　それでは，運動量表示についても考えてみます．1次元の運動量演算子についての固有値方程式は，

	$\displaystyle \hat{p}_{x}\phi_{p_{x}}(x)=p_{x}\phi_{p_{x}}(x)$
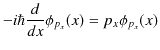$% latex2html id marker 2780 $\displaystyle \therefore$$	$\displaystyle -i\hbar\dfrac{d}{dx}\phi_{p_{x}}(x)=p_{x}\phi_{p_{x}}(x)$
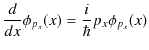$% latex2html id marker 2782 $\displaystyle \therefore$$	$\displaystyle \dfrac{d}{dx}\phi_{p_{x}}(x)=\dfrac{i}{\hbar}p_{x}\phi_{p_{x}}(x)$

となります．この微分方程式を満たす $\phi(\bm{x})$ は，

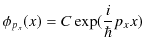
$\displaystyle \phi_{p_{x}}(x)=C\exp(\dfrac{i}{\hbar}p_{x}x)$

となります．（この解を上の微分方程式に代入して下さい．すぐに確かめられますね．）は定数です．3次元に拡張すると，

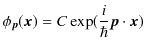
$\displaystyle \phi_{\bm{p}}(\bm{x})=C\exp(\dfrac{i}{\hbar}\bm{p}\cdot\bm{x})$

となります．このとき，

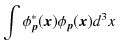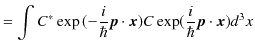$\displaystyle \int\phi_{\bm{p}}^{*}(\bm{x})\phi_{\bm{p}}(\bm{x})d^{3}x$	$\displaystyle =\int C^{*}\exp⁡(-\dfrac{i}{\hbar}\bm{p}\cdot\bm{x})C\exp(\dfrac{i}{\hbar}\bm{p}\cdot\bm{x})d^{3}x$
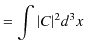	$\displaystyle =\int\vert C\vert^{2}d^{3}x$

となりますが，この積分は発散します．そこで，連続固有関数の場合に取り扱うδ関数規格直交条件を考えましょう．

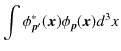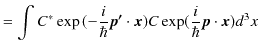$\displaystyle \int\phi_{\bm{p'}}^{*}(\bm{x})\phi_{\bm{p}}(\bm{x})d^{3}x$	$\displaystyle =\int C^{*}\exp⁡(-\dfrac{i}{\hbar}\bm{p'}\cdot\bm{x})C\exp(\dfrac{i}{\hbar}\bm{p}\cdot\bm{x})d^{3}x$
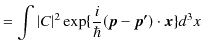	$\displaystyle =\int\vert C\vert^2\exp\{\dfrac{i}{\hbar}(\bm{p}-\bm{p'})\cdot\bm{x}\}d^{3}x$

ここで，δ関数の表式，

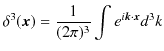
$\displaystyle \delta^{3}(\bm{x})=\dfrac{1}{(2\pi)^{3}}\int e^{i\bm{k}\cdot\bm{x}}d^{3}k$

において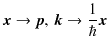， $\bm{x}\to\bm{p},\,\bm{k}\to\dfrac{1}{\hbar}\bm{x}$ と置き換えると，

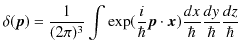	$\displaystyle \delta(\bm{p})=\dfrac{1}{(2\pi)^{3}}\int\exp(\dfrac{i}{\hbar}\bm{p}\cdot\bm{x})\dfrac{dx}{\hbar}\dfrac{dy}{\hbar}\dfrac{dz}{\hbar}$
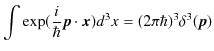$% latex2html id marker 2803 $\displaystyle \therefore$$	$\displaystyle \int\exp(\dfrac{i}{\hbar}\bm{p}\cdot\bm{x})d^{3}x=(2\pi\hbar)^{3}\delta^{3}(\bm{p})$

となります．最後の式を使うと，

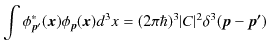
$\displaystyle \int\phi_{\bm{p'}}^{*}(\bm{x})\phi_{\bm{p}}(\bm{x})d^{3}x=(2\pi\hbar)^{3}\vert C\vert^{2}\delta^{3}(\bm{p}-\bm{p'})$

となります．ここで，δ関数規格直交条件，

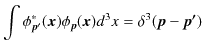
$\displaystyle \int\phi_{\bm{p'}}^{*}(\bm{x})\phi_{\bm{p}}(\bm{x})d^{3}x=\delta^{3}(\bm{p}-\bm{p'})$

が成立しなければならないとします．このとき，

	$\displaystyle (2\pi\hbar)^{3}\vert C\vert^{2}=1$
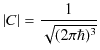$% latex2html id marker 2810 $\displaystyle \therefore$$	$\displaystyle \vert C\vert=\dfrac{1}{\sqrt{(2\pi\hbar)^{3}}}$

となります．したがって運動量演算子の連続固有関数は，

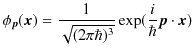
$\displaystyle \phi_{\bm{p}}(\bm{x})=\dfrac{1}{\sqrt{(2\pi\hbar)^{3}}}\exp(\dfrac{i}{\hbar}\bm{p}\cdot\bm{x})$

となります．さらに，アインシュタイン-ド・ブロイの関係式 $\bm{p}=\hbar\bm{k}$ を使うと，

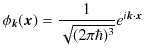
$\displaystyle \phi_{\bm{k}}(\bm{x})=\dfrac{1}{\sqrt{(2\pi\hbar)^{3}}}e^{i\bm{k}\cdot\bm{x}}$

となります．運動量表示では， $\phi_{\bm{k}}(\bm{x})=\frac{1}{\sqrt{(2\pi\hbar)^{3}}}\exp(i\bm{k}\cdot\bm{x})$ を基底にとり，任意の関数 $\psi(t,\bm{x})$ を展開します．

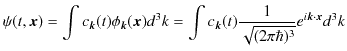
$\displaystyle \psi(t,\bm{x})=\int c_{\bm{k}}(t)\phi_{\bm{k}}(\bm{x})d^{3}k=\int c_{\bm{k}}(t)\dfrac{1}{\sqrt{(2\pi\hbar)^{3}}}e^{i\bm{k}\cdot\bm{x}}d^{3}k$

　このSectionでは，表示の方法，つまり任意の波動関数を固有関数系で展開する場合の基底の選び方について見てきました．ここで，基底の変換について言及しておきます．"数学的準備（δ関数）" のSectionで，δ関数のフーリエ変換とフーリエ逆変換について考えました．3次元フーリエ変換は，

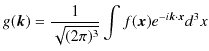
$\displaystyle g(\bm{k})=\dfrac{1}{\sqrt{(2\pi)^{3}}}\int f(\bm{x})e^{-i\bm{k}\cdot\bm{x}}d^{3}x$

であり，3次元フーリエ逆変換は，

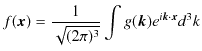
$\displaystyle f(\bm{x})=\dfrac{1}{\sqrt{(2\pi)^{3}}}\int g(\bm{k})e^{i\bm{k}\cdot\bm{x}}d^{3}k$

でした．3次元フーリエ変換で， $f(\bm{x})=\phi_{\bm{x}'}(\bm{x})=\delta^{3}(\bm{x}-\bm{x}')$ をとると，

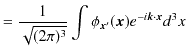$\displaystyle g(\bm{k})$	$\displaystyle =\dfrac{1}{\sqrt{(2\pi)^{3}}}\int\phi_{\bm{x}'}(\bm{x})e^{-i\bm{k}\cdot\bm{x}}d^{3}x$
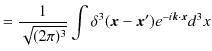	$\displaystyle =\dfrac{1}{\sqrt{(2\pi)^{3}}}\int\delta^{3}(\bm{x}-\bm{x}')e^{-i\bm{k}\cdot\bm{x}}d^{3}x$
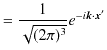	$\displaystyle =\dfrac{1}{\sqrt{(2\pi)^{3}}}e^{-i\bm{k}\cdot\bm{x}'}$
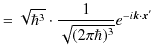	$\displaystyle =\sqrt{\hbar^{3}}\cdot\dfrac{1}{\sqrt{(2\pi\hbar)^{3}}}e^{-i\bm{k}\cdot\bm{x}'}$
	$\displaystyle =\sqrt{\hbar^{3}}\phi_{\bm{-k}}(\bm{x}')$

となり，位置表示の基底をフーリエ変換すると，運動量表示の基底になることが理解されます．一方，3次元フーリエ逆変換で， $g(\bm{k})=\phi_{-\bm{k}}(\bm{x}')=\frac{1}{\sqrt{(2\pi\hbar)^{3}}}\exp(-i\bm{k}\cdot\bm{x}')$ をとると，

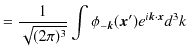$\displaystyle f(\bm{x})$	$\displaystyle =\dfrac{1}{\sqrt{(2\pi)^{3}}}\int\phi_{-\bm{k}}(\bm{x}')e^{i\bm{k}\cdot\bm{x}}d^{3}k$
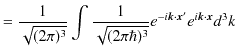	$\displaystyle =\dfrac{1}{\sqrt{(2\pi)^{3}}}\int\dfrac{1}{\sqrt{(2\pi\hbar)^{3}}}e^{-i\bm{k}\cdot\bm{x}'}e^{i\bm{k}\cdot\bm{x}}d^{3}k$
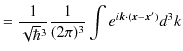	$\displaystyle =\dfrac{1}{\sqrt{\hbar}^{3}}\dfrac{1}{(2\pi)^{3}}\int e^{i\bm{k}\cdot(\bm{x}-\bm{x}')}d^{3}k$
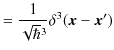	$\displaystyle =\dfrac{1}{\sqrt{\hbar}^{3}}\delta^{3}(\bm{x}-\bm{x}')$
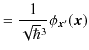	$\displaystyle =\dfrac{1}{\sqrt{\hbar}^{3}}\phi_{\bm{x}'}(\bm{x})$

が確かめられます．このように，運動量表示の基底をフーリエ逆変換したものは，位置表示の基底になることが理解されますね．

9.5 併立するオブザーバブル

これから2つのSectionで演算子の交換関係について成立する定理を与えておきます．オブザーバブルが2つある場合について，次の定理が成立します．

定理9.2 " $[\hat{A},\hat{B}]\Leftrightarrow$ $\hat{A}$ の固有状態と $\hat{B}$ の固有状態は同時固有状態をなします．"

同時固有状態とは，その状態が $\hat{A}$ の固有状態でもあり， $\hat{B}$ の固有状態でもある量子状態のことです．

　まず，（ $\Rightarrow$ ）向きの証明を実行します． $\hat{A}$ と $\hat{B}$ が交換可能なので，

$\displaystyle \hat{A}\hat{B}=\hat{B}\hat{A}$

が成り立ちます．この演算子を $\hat{A}$ の固有状態 $\phi_{a}(\bm{x})$ に作用させます．

$\displaystyle \hat{A}\hat{B}\phi_{a}(\bm{x})$	$\displaystyle =\hat{B}\hat{A}\phi_{a}(\bm{x})$
	$\displaystyle =a\hat{B}\phi_{a}(\bm{x})$

故に， $\hat{B}\phi_{a}(\bm{x})$ は演算子 $\hat{A}$ の固有状態になっています．したがって， $\hat{B}\phi_{a}(\bm{x})$ は $\phi_{a}(\bm{x})$ の定数倍になるはずです．

$\displaystyle \hat{B}\phi_{a}(\bm{x})=b\phi_{a}(\bm{x})$

この式は， $\hat{A}$ の固有状態 $\phi_{a}(\bm{x})$ が $\hat{B}$ の固有状態であることを示しています．つまり， $\hat{A}$ の固有状態と $\hat{B}$ の固有状態が同時固有状態であることが証明されました．

　次に，逆方向（ $\Leftarrow$ ）について証明します．まず， $\hat{A}$ と $\hat{B}$ の同時固有状態 $\phi_{n}(\bm{x})$ に交換子 $[\hat{A},\hat{B}]$ を作用させます．

$\displaystyle [\hat{A},\hat{B}]\phi_{n}(\bm{x})$	$\displaystyle =(\hat{A}\hat{B}-\hat{B}\hat{A})\phi_{n}(\bm{x})$
	$\displaystyle =(a_{n}b_{n}-b_{n}a_{n})\phi_{n}(\bm{x})$
	$\displaystyle =0$

ここで，について和をとります．

	$\displaystyle \sum_{n=1}^{\infty}[\hat{A},\hat{B}]\phi_{n}(\bm{x})=0$
$% latex2html id marker 2912 $\displaystyle \therefore$$	$\displaystyle [\hat{A},\hat{B}]\sum_{n=1}^{\infty}\phi_{n}(\bm{x})=0$

ここで，

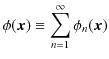
$\displaystyle \phi(\bm{x})\equiv\sum_{n=1}^{\infty}\phi_{n}(\bm{x})$

とおくと，

$\displaystyle [\hat{A},\hat{B}]\phi(\bm{x})=0$

となりますが，任意の $\phi(\bm{x})$ について成立すると仮定すると，

$\displaystyle [\hat{A},\hat{B}]=0$

となります．よって，定理は証明されました．

9.6 併立しないオブザーバブル

2つのオブザーバブル（演算子）が非可換の場合，次の定理が成立します．

定理9.3

$\displaystyle [\hat{A},\hat{B}]\neq0\Rightarrow\Delta A\cdot\Delta B\geqq\dfrac{1}{2}\vert\langle[\hat{A},\hat{B}]\rangle\vert$

$\Delta A$ と $\Delta B$ は理想測定値の不確定性を表します．また，右辺の絶対値の中の記号は演算子の期待値でした．この定理は，不確定性原理のChapterにおいて思考実験で導いておいた原理を一般的に表したものです．具体例として，位置と運動量の間の不確定性を挙げておきます．（1次元で考えています．）交換関係，

$\displaystyle [\hat{x},\hat{p}_{x}]=i\hbar$

が成立しましたので，

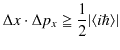	$\displaystyle \Delta x\cdot\Delta p_{x}\geqq\dfrac{1}{2}\vert\langle i\hbar\rangle\vert$
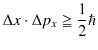$% latex2html id marker 2937 $\displaystyle \therefore$$	$\displaystyle \Delta x\cdot\Delta p_{x}\geqq\dfrac{1}{2}\hbar$

が成り立ちます．最後の式が，位置と運動量の不確定性原理の正確な表式です．それでは，もとの一般的な定理を証明しましょう．まず，2つのエルミート演算子を定義します．

	$\displaystyle \hat{\alpha}\equiv\hat{A}-\langle\hat{A}\rangle$
	$\displaystyle \hat{\beta}\equiv\hat{B}-\langle\hat{B}\rangle$

ここで，次の状態 $\chi(\bm{x})$ をつくります．

$\displaystyle \chi=(\hat{\alpha}+i\lambda\hat{\beta})\phi(\bm{x})$

ただし， $\lambda$ は実数とします．ここで，状態の絶対値の2乗は 0 以上なので， $\chi(\bm{x})$ について次の式が成立します．

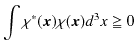
$\displaystyle \int\chi^{*}(\bm{x})\chi(\bm{x})d^{3}x\geqq0$

$\chi(\bm{x})$ に上述の式を代入して計算します．

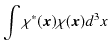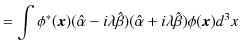$\displaystyle \int\chi^{*}(\bm{x})\chi(\bm{x})d^{3}x$	$\displaystyle =\int\phi^{*}(\bm{x})(\hat{\alpha}-i\lambda\hat{\beta})(\hat{\alpha}+i\lambda\hat{\beta})\phi(\bm{x})d^{3}x$
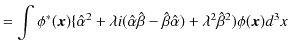	$\displaystyle =\int\phi^{*}(\bm{x})\{\hat{\alpha}^{2}+\lambda i(\hat{\alpha}\hat{\beta}-\hat{\beta}\hat{\alpha})+\lambda^{2}\hat{\beta}^{2})\phi(\bm{x})d^{3}x$
	$\displaystyle =\langle\hat{\beta}^{2}\rangle\lambda^{2}+\langle i[\hat{\alpha},\hat{\beta}]\rangle\lambda+\langle\hat{\alpha}^{2}\rangle\geqq0$

最後の不等式を変形していきます．

	$\displaystyle \langle\hat{\beta}^{2}\rangle(\lambda^{2}+2\dfrac{\langle i[\hat{... ...gle\hat{\beta}^{2}\rangle-\langle i[\hat{\alpha},\hat{\beta}]\rangle^{2})\geqq0$
$% latex2html id marker 2959 $\displaystyle \therefore$$	$\displaystyle \langle\hat{\beta}^{2}\rangle(\lambda+\dfrac{\langle i[\hat{\alph... ...angle\langle\hat{\beta}^{2}\rangle-\langle i[\hat{A},\hat{B}]\rangle^{2})\geqq0$

最後の不等式が常に成立するためには，最小値，

$\displaystyle \dfrac{1}{4\langle\hat{\beta}^{2}\rangle}(4\langle\hat{\alpha}^2\rangle\langle\hat{\beta}^{2}\rangle-\langle i[\hat{A},\hat{B}]\rangle^{2})$

が 0 以上にならなければなりません．よって，

	$\displaystyle 4\langle\hat{\alpha}^2\rangle\langle\hat{\beta}^{2}\rangle-\langle i[\hat{A},\hat{B}]\rangle^{2}\geqq0$
$% latex2html id marker 2965 $\displaystyle \therefore$$	$\displaystyle 2\sqrt{\langle\hat{\alpha}^{2}\rangle}\sqrt{\langle\hat{\beta}^{2}\rangle}\geqq\vert\langle i[\hat{A},\hat{B}]\rangle\vert$
$% latex2html id marker 2967 $\displaystyle \therefore$$	$\displaystyle \Delta A\cdot\Delta B\geqq\dfrac{1}{2}\vert\langle[\hat{A},\hat{B}]\rangle\vert$

が成立します．（証明終．）

　前のSectionとこのSectionの定理により，次の事項が理解されます．すなわち，2つのオブザーバブルが交換可能の場合は量子状態が同時固有状態になり，2つのオブザーバブルに対して，同時に不確定性なしに理論値の計算ができます．それに対して，2つのオブザーバブルが交換不可能の場合は，2つのオブザーバブルの間に不確定性関係が成立し，同時に正確な理論値を得ることができません．

　このChapterまで波動力学の一般論を述べてきました．次の4つのChapterでは具体例を取り扱っていきたいと思います．