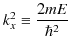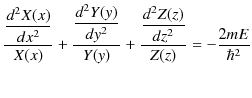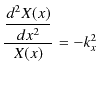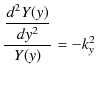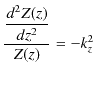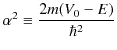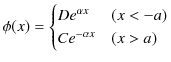J Simplicity 束縛状態1（例1: 自由粒子と井戸型ポテンシャル）

Chapter10 束縛状態1（例1: 自由粒子と井戸型ポテンシャル）

10.1 1次元無限空間の中の自由粒子

前のChapterまで，波動力学の一般論を展開しました．このChapterから具体例を取り扱うことにします．最も簡単な例は，1個の自由粒子だと考えられます．自由という意味は電場や磁場などの外場がなく，他のいずれとも相互作用しないということです．言い直すとポテンシャルは 0 になります．自由粒子の粒子というのは，量子のことを意味し，例えば電子などを想像して下さい．ここで，簡単のため，空間次元は1次元と限定します．もとになる時間に依存しないシュレディンガー方程式は，

$\displaystyle \hat{H}(\bm{x},-i\hbar\bm{\nabla})\phi(\bm{x})=E\phi(\bm{x})$

ですが，一般に，ハミルトニアンは，

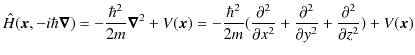
$\displaystyle \hat{H}(\bm{x},-i\hbar\bm{\nabla})=-\dfrac{\hbar^{2}}{2m}\bm{\nab... ...c{\partial^{2}}{\partial y^{2}}+\dfrac{\partial^{2}}{\partial z^{2}})+V(\bm{x})$

と与えられています．今考えている，空間次元が1次元でポテンシャルが 0 の場合は，ハミルトニアンは，

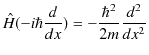
$\displaystyle \hat{H}(-i\hbar\dfrac{d}{dx})=-\dfrac{\hbar^{2}}{2m}\dfrac{d^{2}}{dx^{2}}$

となります．したがって，解くべきシュレディンガー方程式は，

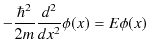
$\displaystyle -\dfrac{\hbar^{2}}{2m}\dfrac{d^{2}}{dx^{2}}\phi(x)=E\phi(x)$

となります．これを少し変形します．

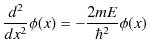
$\displaystyle \dfrac{d^{2}}{dx^{2}}\phi(x)=-\dfrac{2mE}{\hbar^{2}}\phi(x)$

ここで，自由粒子のエネルギーは正なので，

$\displaystyle k_{x}^{2}\equiv\dfrac{2mE}{\hbar^{2}}$

(10.1)

とおくと，方程式は，

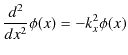
$\displaystyle \dfrac{d^{2}}{dx^{2}}\phi(x)=-k_{x}^{2}\phi(x)$

となります．この微分方程式は固有値方程式です．以下，解法を示しておくことにします．

$\displaystyle \phi(x)=\alpha e^{\lambda x}$

とおき，微分方程式に代入します．（ $\alpha$ と $\lambda$ は複素数の定数とします．）

	$\displaystyle \alpha\lambda^{2}e^{\lambda x}=-k_{x}^{2}\alpha e^{\lambda x}$
$% latex2html id marker 1923 $\displaystyle \therefore$$	$\displaystyle \lambda^{2}=-k_{x}^{2}$
$% latex2html id marker 1925 $\displaystyle \therefore$$	$\displaystyle \lambda=\pm ik_{x}$

故に，解は，

$\displaystyle \phi(x)=\alpha_{1}e^{ik_{x}x}+\alpha_{2}e^{-ik_{x}x}$

(10.2)

となります．さらに，複素数の指数関数を3角関数で表して計算します．

$\displaystyle \phi(x)$	$\displaystyle =\alpha_{1}(\cos k_{x}x+i\sin k_{x}x)+\alpha_{2}(\cos k_{x}x-i\sin k_{x}x)$
	$\displaystyle =(\alpha_{1}-\alpha_{2})i\sin k_{x}x+(\alpha_{1}+\alpha_{2})\cos k_{x}x$

ここで，2つの複素数の定数を導入して，

	$\displaystyle A\equiv(\alpha_{1}-\alpha_{2})i$
	$\displaystyle B\equiv\alpha_{1}+\alpha_{2}$

とおくと，

$\displaystyle \phi(x)=A\sin k_{x}x+B\cos k_{x}x$

(10.3)

という一般解が得られます．（波動関数は一般に複素数の関数でしたね．）この波動関数 $\phi(x)$ が1次元空間いっぱいに広がっていて，粒子はどこにあるかは，観測前はわかりません．（2重性の中の波動性が現れています．）ただその存在確率のみ計算することができるのです．このような状況の中で，観測という行為を行うと波動関数が量子飛躍し，1次元の全空間の中のどこかに電子が発見されます．（粒子性が現れます．）

　ここで，注意しなければならないことがあります．今，1次元空間は負の無限大から正の無限大にとってあるので，規格化条件を計算すると無限大になってしまうということです．実際に計算してみます．（(10.2)式の一般解を使います．）

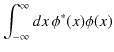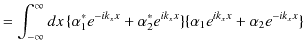$\displaystyle \int_{-\infty}^{\infty}dx\,\phi^{*}(x)\phi(x)$	$\displaystyle =\int_{-\infty}^{\infty}dx\,\{\alpha_{1}^{}e^{-ik_{x}x}+\alpha_{2}^{}e^{ik_{x}x}\}\{\alpha_{1}e^{ik_{x}x}+\alpha_{2}e^{-ik_{x}x}\}$
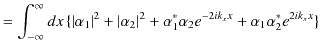	$\displaystyle =\int_{-\infty}^{\infty}dx\,\{\vert\alpha_{1}\vert^{2}+\vert\alph... ...2}+\alpha_{1}^{}\alpha_{2}e^{-2ik_{x}x}+\alpha_{1}\alpha_{2}^{}e^{2ik_{x}x}\}$
	$\displaystyle =[(\vert\alpha_{1}\vert^{2}+\vert\alpha_{2}\vert^{2})x+\dfrac{1}{... ...pha_{2}e^{-2ik_{x}x}+\alpha_{1}\alpha_{2}^{*}e^{2ik_{x}x}\}]_{-\infty}^{\infty}$
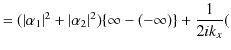	$\displaystyle =(\vert\alpha_{1}\vert^{2}+\vert\alpha_{2}\vert^{2})\{\infty-(-\infty)\}+\dfrac{1}{2ik_{x}}($ 有限値 $\displaystyle )$
	$\displaystyle =\infty$

このことは，1次元全宇宙空間に1個の自由粒子が存在していた場合，波動関数は遠方でも減衰しないため，無限遠から無限遠まで存在確率は 0 ではないことを反映しています．しかし，全体の存在確率がではなく，無限大になってしまう状況は，物理的に意味がありません．次のSectionで回避策を考えましょう．

10.2 1次元箱の中の自由粒子

存在確率の無限大を避ける簡単な方法は，量子を箱の中に入れることです．今考えているのは1次元ですから，箱というのは，この場合線分になります．（以下，この線分のことを箱ということにします．）この箱の中に量子状態を表す波動関数が存在しています．その解は，前Sectionの(10.3)式より，

$\displaystyle \phi(x)=A\sin k_{x}x+B\cos k_{x}x$

であることがわかっています．量子は箱の中に存在しているので，その箱の中以外での存在確率は 0 になります．したがって，量子状態を表す波動関数も箱の中以外では 0 の値をとります．一般に，波動関数に関しては，座標についてなめらかな連続関数でなければならないという条件が付きます．つまり， $\phi(x)$ とその1階微分の $\phi'(x)$ が至る所で連続でなければなりません．しかし，この場合，箱の外は完全に存在確率 0 としているので，境界でなめらかなという条件，すなわち $\phi'(x)$ が連続であるという条件は成立しません．そこで，箱の境界で $\phi(x)$ が連続であるという条件のみを書くと，次のようになります．（微分方程式を解く場合，ニュートン力学では初期条件を使いましたが，波動力学では，このように境界での条件である境界条件を使います．）

$\displaystyle \phi(0)=\phi(L)=0$

1次元の箱の長さをにして，0 からまでの領域に箱を置きました．この境界条件を(10.3)式の一般解に適用します． $\phi(0)=0$ より，

	$\displaystyle \phi(0)=A\cdot0+B\cdot1=0$
$% latex2html id marker 1972 $\displaystyle \therefore$$	$\displaystyle B=0$
$% latex2html id marker 1974 $\displaystyle \therefore$$	$\displaystyle \phi(x)=A\sin k_{x}x$

となります．さらに， $\phi(L)=0$ より，

$\displaystyle \phi(L)=A\sin k_{x}L=0$

となります．ここで，とすると，波動関数が恒等的に 0 になってしまい，不適となります．したがって，

	$\displaystyle \sin k_{x}L=0$
$% latex2html id marker 1984 $\displaystyle \therefore$$	$\displaystyle k_{x}L=n\pi$
$% latex2html id marker 1986 $\displaystyle \therefore$$	$\displaystyle k_{x}=\dfrac{n\pi}{L}$

となります．ここで，は整数です．故に，固有関数は，

$\displaystyle \phi_{n}(x)=A\sin(\dfrac{n\pi}{L}x)$

と表せ，定常波を形成していることが理解できます．また，このように波動関数が実数のこともあります．（この固有関数は離散固有関数であることがわかります．したがって，量子状態は束縛状態ということになりますね．）とすると，波動関数が座標によらずに 0 になり，意味のある量子状態になりません．また， $n=-1,-2,\cdots$ などは， $n=1,2,\cdots$ のときの逆符号になるだけで，独立な解にはなりません．よって， $n=1,2,\cdots$ とします．（を量子数といいます．）の状態を基底状態といい， $n=2,3,\cdots$ の状態を励起状態といいます．また，離散エネルギー固有値は，(10.1)式より，

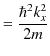$\displaystyle E_{n}$	$\displaystyle =\dfrac{\hbar^{2}k_{x}^{2}}{2m}$
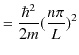	$\displaystyle =\dfrac{\hbar^{2}}{2m}(\dfrac{n\pi}{L})^{2}$
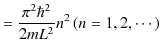	$\displaystyle =\dfrac{\pi^{2}\hbar^{2}}{2mL^{2}}n^{2}\,(n=1,2,\cdots)$

となり，跳び跳びの値をもちます．エネルギー固有値は，のとき最小値をとりますが，0 にはなりません．これを零点エネルギーといいます．絶対零度の場合でもエネルギーは 0 ではないのです．このことは古典的には考えられない，波動力学の特徴です．

　次に，箱（1次元の線分）の全領域における存在確率がであるという規格化条件を適用して，定数を決定します．

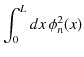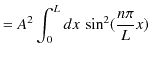$\displaystyle \int_{0}^{L}dx\,\phi_{n}^{2}(x)$	$\displaystyle =A^{2}\int_{0}^{L}dx\,\sin^{2}(\dfrac{n\pi}{L}x)$
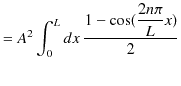	$\displaystyle =A^{2}\int_{0}^{L}dx\,\dfrac{1-\cos(\dfrac{2n\pi}{L}x)}{2}$
	$\displaystyle =A^{2}[\dfrac{x}{2}-\dfrac{L}{4n\pi}\sin(\dfrac{2n\pi}{L}x)]_{0}^{L}$
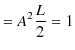	$\displaystyle =A^{2}\dfrac{L}{2}=1$

となりますので，故に，

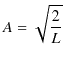	$\displaystyle A=\sqrt{\dfrac{2}{L}}$
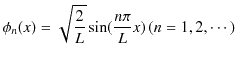$% latex2html id marker 2025 $\displaystyle \therefore$$	$\displaystyle \phi_{n}(x)=\sqrt{\dfrac{2}{L}}\sin(\dfrac{n\pi}{L}x)\,(n=1,2,\cdots)$

となります．最後の式が規格化された離散固有関数になります．したがって，存在確率密度は，

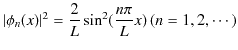
$\displaystyle \vert\phi_{n}(x)\vert^{2}=\dfrac{2}{L}\sin^{2}(\dfrac{n\pi}{L}x)\,(n=1,2,\cdots)$

になります．さらに，量子数の異なる離散固有関数が直交することを確かめておきます． $n\neq m$ のとき，

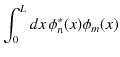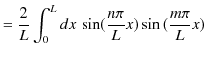$\displaystyle \int_{0}^{L}dx\,\phi_{n}^{*}(x)\phi_{m}(x)$	$\displaystyle =\dfrac{2}{L}\int_{0}^{L}dx\,\sin(\dfrac{n\pi}{L}x)\sin⁡(\dfrac{m\pi}{L}x)$
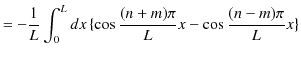	$\displaystyle =-\dfrac{1}{L}\int_{0}^{L}dx\,\{\cos\dfrac{(n+m)\pi}{L}x-\cos\dfrac{(n-m)\pi}{L}x\}$
	$\displaystyle =-\dfrac{1}{L}[\dfrac{L}{(n+m)\pi}\sin\dfrac{(n+m)\pi}{L}x-\dfrac{L}{(n-m)\pi}\sin\dfrac{(n-m)\pi}{L}x]_{0}^{L}$
	$\displaystyle =0$

となります．まとめると，離散固有関数は規格直交条件，

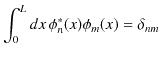
$\displaystyle \int_{0}^{L}dx\,\phi_{n}^{*}(x)\phi_{m}(x)=\delta_{nm}$

を満たし，規格直交系を成すということが確認されました．ただし，右辺の記号は，クロネッカーのデルタで，

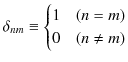
$\displaystyle \delta_{nm}\equiv\begin{cases} 1 & (n=m)\\ 0 & (n\neq m) \end{cases}$

で定義されます．

10.3 3次元箱の中の自由粒子

空間を1次元にすることは，状況を簡単にして，また計算をしやすくするというメリットがありますが，現実の空間は3次元です．そこで，3次元の箱の中にある1個の自由粒子を考えていきましょう．箱は立方体の場合を考え，デカルト座標で，,,,,,,, を頂点にとります．もとになる時間に依存しないシュレディンガー方程式は，

$\displaystyle \hat{H}(\bm{x},-i\hbar\bm{\nabla})\phi(\bm{x})=E\phi(\bm{x})$

で，ハミルトニアンは，

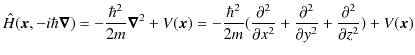
$\displaystyle \hat{H}(\bm{x},-i\hbar\bm{\nabla})=-\dfrac{\hbar^{2}}{2m}\bm{\nab... ...c{\partial^{2}}{\partial y^{2}}+\dfrac{\partial^{2}}{\partial z^{2}})+V(\bm{x})$

でした．ここで，自由粒子を扱いますので，ポテンシャルは 0 です．したがって，シュレディンガー方程式は，

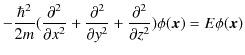
$\displaystyle -\dfrac{\hbar^{2}}{2m}(\dfrac{\partial^{2}}{\partial x^{2}}+\dfra... ...\partial y^{2}}+\dfrac{\partial^{2}}{\partial z^{2}})\phi(\bm{x})=E\phi(\bm{x})$

となります．この微分方程式を変数分離の方法で解くことにします．すなわち，波動関数 $\phi(\bm{x})$ を，

$\displaystyle \phi(\bm{x})\equiv X(x)Y(y)Z(z)$

とし，のそれぞれの関数の積であるとします．このとき，微分方程式は，

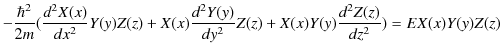
$\displaystyle -\dfrac{\hbar^{2}}{2m}(\dfrac{d^{2}X(x)}{dx^{2}}Y(y)Z(z)+X(x)\dfrac{d^{2}Y(y)}{dy^{2}}Z(z)+X(x)Y(y)\dfrac{d^{2}Z(z)}{dz^{2}})=EX(x)Y(y)Z(z)$

となります．この方程式の両辺をで割り，変形すると，

$\displaystyle \dfrac{\dfrac{d^{2}X(x)}{dx^{2}}}{X(x)}+\dfrac{\dfrac{d^{2}Y(y)}{dy^{2}}}{Y(y)}+\dfrac{\dfrac{d^{2}Z(z)}{dz^{2}}}{Z(z)}=-\dfrac{2mE}{\hbar^{2}}$

(10.4)

となります．最後の式で，左辺第1項はだけの関数，左辺第2項はだけの関数，左辺第3項はだけの関数です．そして，この3つの項の和が右辺の定数に等しいということは，それぞれの項が定数でなければならないということになります．ここで，方向，方向，方向については特別な方向がなく，3方向は同等な方向であることに注意しましょう．右辺の定数が負の値をとっているということは，左辺のそれぞれの項も負の定数になります．そこで，

	$\displaystyle \dfrac{\dfrac{d^{2}X(x)}{dx^{2}}}{X(x)}=-k_{x}^{2}$	(10.5)
	$\displaystyle \dfrac{\dfrac{d^{2}Y(y)}{dy^{2}}}{Y(y)}=-k_{y}^{2}$	(10.6)
	$\displaystyle \dfrac{\dfrac{d^{2}Z(z)}{dz^{2}}}{Z(z)}=-k_{z}^{2}$	(10.7)

と置くことができます．故に，

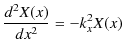	$\displaystyle \dfrac{d^{2}X(x)}{dx^{2}}=-k_{x}^{2}X(x)$
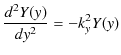	$\displaystyle \dfrac{d^{2}Y(y)}{dy^{2}}=-k_{y}^{2}Y(y)$
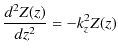	$\displaystyle \dfrac{d^{2}Z(z)}{dz^{2}}=-k_{z}^{2}Z(z)$

という微分方程式が導かれます．これは前Sectionの1次元箱の中の自由粒子と全く同じ方程式で，境界条件もそれぞれの変数について 0 からまでと同じになっています．よって，解は，

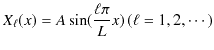	$\displaystyle X_{\ell}(x)=A\sin(\dfrac{\ell\pi}{L}x)\,(\ell=1,2,\cdots)$
	$\displaystyle Y_{m}(y)=B\sin(\dfrac{m\pi}{L}y)\,(m=1,2,\cdots)$
	$\displaystyle Z_{n}(z)=C\sin(\dfrac{n\pi}{L}z)\,(n=1,2,\cdots)$

となります．全体の波動関数は，をあらためてと置きなおして，

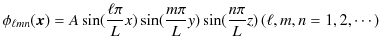
$\displaystyle \phi_{\ell mn}(\bm{x})=A\sin(\dfrac{\ell\pi}{L}x)\sin(\dfrac{m\pi}{L}y)\sin(\dfrac{n\pi}{L}z)\,(\ell,m,n=1,2,\cdots)$

となります．次に，規格化条件から定数の値を決定します．

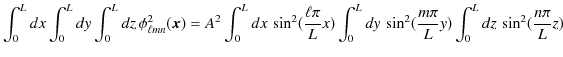
$\displaystyle \int_{0}^{L}dx\int_{0}^{L}dy\int_{0}^{L}dz\,\phi_{\ell mn}^{2}(\b... ...{0}^{L}dy\,\sin^{2}(\dfrac{m\pi}{L}y)\int_{0}^{L}dz\,\sin^{2}(\dfrac{n\pi}{L}z)$

ここで，

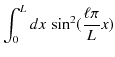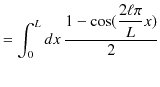$\displaystyle \int_{0}^{L}dx\,\sin^{2}(\dfrac{\ell\pi}{L}x)$	$\displaystyle =\int_{0}^{L}dx\,\dfrac{1-\cos(\dfrac{2\ell\pi}{L}x)}{2}$
	$\displaystyle =[\dfrac{x}{2}-\dfrac{L}{4\ell\pi}\sin(\dfrac{2\ell\pi}{L}x)]_{0}^{L}$
	$\displaystyle =\dfrac{L}{2}$

なので，

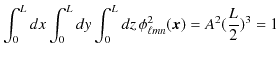	$\displaystyle \int_{0}^{L}dx\int_{0}^{L}dy\int_{0}^{L}dz\,\phi_{\ell mn}^{2}(\bm{x})=A^{2}(\dfrac{L}{2})^{3}=1$
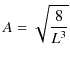$% latex2html id marker 2115 $\displaystyle \therefore$$	$\displaystyle A=\sqrt{\dfrac{8}{L^{3}}}$

となります．まとめると固有関数は，

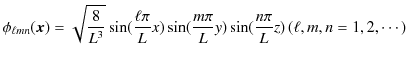
$\displaystyle \phi_{\ell mn}(\bm{x})=\sqrt{\dfrac{8}{L^{3}}}\sin(\dfrac{\ell\pi}{L}x)\sin(\dfrac{m\pi}{L}y)\sin(\dfrac{n\pi}{L}z)\,(\ell,m,n=1,2,\cdots)$

となり，定常波を形成していることが理解できます．また，エネルギー固有値は，(10.4)式，(10.5)式，(10.6)式，(10.7)式より，

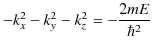	$\displaystyle -k_{x}^{2}-k_{y}^{2}-k_{z}^{2}=-\dfrac{2mE}{\hbar^{2}}$
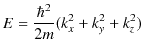$% latex2html id marker 2120 $\displaystyle \therefore$$	$\displaystyle E=\dfrac{\hbar^{2}}{2m}(k_{x}^{2}+k_{y}^{2}+k_{z}^{2})$
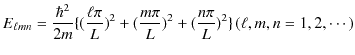$% latex2html id marker 2122 $\displaystyle \therefore$$	$\displaystyle E_{\ell mn}=\dfrac{\hbar^{2}}{2m}\{(\dfrac{\ell\pi}{L})^{2}+(\dfrac{m\pi}{L})^{2}+(\dfrac{n\pi}{L})^{2}\}\,(\ell,m,n=1,2,\cdots)$

と求められます． $\ell=m=n=1$ の場合が基底状態，それ以外の基底状態よりエネルギーの高い状態が励起状態です．

　箱の中に1個の量子が自由に存在している場合，観測前は波動関数 $\phi(\bm{x})$ が箱一杯に定常波を形成して広がっています．波動性が現れていて，粒子性は表に出てきません．ここで，何らかの方法で観測すると量子飛躍が起こり，箱の中のどこかに粒子が1個見つかります．（粒子性の現れ．）観測の前後に因果関係はなく，波動関数からその存在確率のみを計算することができるのです．実際に，存在確率密度を計算すると，

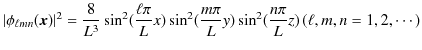
$\displaystyle \vert\phi_{\ell mn}(\bm{x})\vert^{2}=\dfrac{8}{L^{3}}\sin^{2}(\df... ...L}x)\sin^{2}(\dfrac{m\pi}{L}y)\sin^{2}(\dfrac{n\pi}{L}z)\,(\ell,m,n=1,2,\cdots)$

になります．

10.4 1次元井戸型ポテンシャルとシュレディンガー方程式

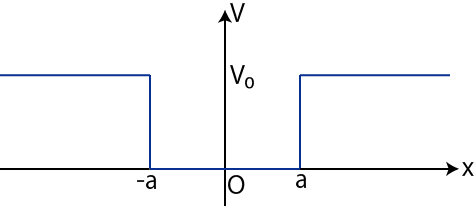
井戸型ポテンシャル

Figure10.1: 井戸型ポテンシャル

1次元井戸型ポテンシャルとは，図のような形をしたポテンシャルです．式で書くと，

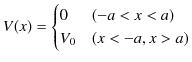
$\displaystyle V(x)=\begin{cases} 0 & (-a<x<a)\\ V_{0} & (x<-a,x>a) \end{cases}$

となります．ただし，と $V_{0}$ は正の定数です．このポテンシャルの中に1個の量子（例えば電子．）がある状況を考えましょう．この量子のエネルギーが $V_{0}$ より小さく正の場合を取り扱ってみます．

$\displaystyle 0<E<V_{0}$

　それでは，この系について時間に依存しないシュレディンガー方程式を立てましょう．もとになる時間に依存しないシュレディンガー方程式は，

$\displaystyle \hat{H}(\bm{x},-i\hbar\bm{\nabla})\phi(\bm{x})=E\phi(\bm{x})$

ですが，一般に，ハミルトニアンは，

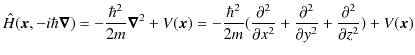
$\displaystyle \hat{H}(\bm{x},-i\hbar\bm{\nabla})=-\dfrac{\hbar^{2}}{2m}\bm{\nab... ...c{\partial^{2}}{\partial y^{2}}+\dfrac{\partial^{2}}{\partial z^{2}})+V(\bm{x})$

と与えられています．1次元の系では，方向のみが関係してきます．

　ここで，の領域を考えます．ポテンシャルの値が 0 なので，ハミルトニアンは，

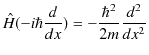
$\displaystyle \hat{H}(-i\hbar\dfrac{d}{dx})=-\dfrac{\hbar^{2}}{2m}\dfrac{d^{2}}{dx^{2}}$

となります．したがって，解くべきシュレディンガー方程式は，

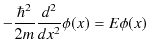
$\displaystyle -\dfrac{\hbar^{2}}{2m}\dfrac{d^{2}}{dx^{2}}\phi(x)=E\phi(x)$

となります．これを少し変形します．

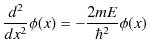
$\displaystyle \dfrac{d^{2}}{dx^{2}}\phi(x)=-\dfrac{2mE}{\hbar^{2}}\phi(x)$

ここで，量子のエネルギーは正なので，

$\displaystyle k_{x}^{2}\equiv\dfrac{2mE}{\hbar^{2}}$

(10.8)

とおくと，方程式は，

$\displaystyle \dfrac{d^{2}}{dx^{2}}\phi(x)=-k_{x}^{2}\phi(x)$

(10.9)

となります．

　次に，の領域を見てみます．1次元なので方向のみ関係し，ポテンシャルの値は定数 $V_{0}$ なので，ハミルトニアンは，

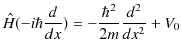
$\displaystyle \hat{H}(-i\hbar\dfrac{d}{dx})=-\dfrac{\hbar^{2}}{2m}\dfrac{d^{2}}{dx^{2}}+V_{0}$

となります．したがって，シュレディンガー方程式は，

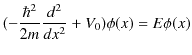
$\displaystyle (-\dfrac{\hbar^{2}}{2m}\dfrac{d^{2}}{dx^{2}}+V_{0})\phi(x)=E\phi(x)$

となります．この式を変形していきます．

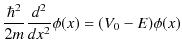	$\displaystyle \dfrac{\hbar^{2}}{2m}\dfrac{d^{2}}{dx^{2}}\phi(x)=(V_{0}-E)\phi(x)$
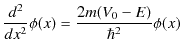$% latex2html id marker 2179 $\displaystyle \therefore$$	$\displaystyle \dfrac{d^{2}}{dx^{2}}\phi(x)=\dfrac{2m(V_{0}-E)}{\hbar^{2}}\phi(x)$

ここで， $E<V_{0}$ なので，右辺の係数は正になります．そこで，

$\displaystyle \alpha^{2}\equiv\dfrac{2m(V_{0}-E)}{\hbar^{2}}$

(10.10)

とおくことができます．解くべき固有値方程式は，

$\displaystyle \dfrac{d^{2}}{dx^{2}}\phi(x)=\alpha^{2}\phi(x)$

(10.11)

となります．

10.5 シュレディンガー方程式の解とパリティ

前のSectionの2つの固有値方程式の解を求めましょう．の領域における(10.9)式は，自由粒子の微分方程式と全く同じ方程式なので，解(10.3)式，

$\displaystyle \phi(x)=A\sin k_{x}x+B\cos k_{x}x$

を持ちます．ただし，とは定数です．

　次に，の領域を考えます．この場合の固有値方程式(10.11)式，

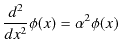
$\displaystyle \dfrac{d^{2}}{dx^{2}}\phi(x)=\alpha^{2}\phi(x)$

を解きます．

$\displaystyle \phi(x)=\beta e^{\lambda x}$

とおき，微分方程式(10.11)式に代入します．（ $\beta$ と $\lambda$ は複素数の定数とします．）

	$\displaystyle \beta\lambda^{2}e^{\lambda x}=\alpha^{2}\beta e^{\lambda x}$
$% latex2html id marker 2207 $\displaystyle \therefore$$	$\displaystyle \lambda^{2}=\alpha^{2}$
$% latex2html id marker 2209 $\displaystyle \therefore$$	$\displaystyle \lambda=\pm\alpha$

故に，解は，

$\displaystyle \phi(x)=Ce^{-\alpha x}+De^{\alpha x}$

となります．（とは定数です．）ここで，の領域では， $x\to-\infty$ において $\phi(x)$ が発散しないという境界条件より，になります．同様に，の領域では， $x\to+\infty$ において $\phi(x)$ が発散しないという境界条件より，になります．まとめると，

$\displaystyle \phi(x)=\begin{cases} De^{\alpha x} & (x<-a)\\ Ce^{-\alpha x} & (x>a) \end{cases}$

(10.12)

となります．

　次に，1次元井戸型ポテンシャルの問題について，パリティという概念を導入します．1次元井戸型ポテンシャルが偶関数であることに注意しましょう．（．）時間に依存しない1次元シュレディンガー方程式，

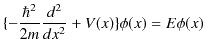
$\displaystyle \{-\dfrac{\hbar^{2}}{2m}\dfrac{d^{2}}{dx^{2}}+V(x)\}\phi(x)=E\phi(x)$

において， $x\to-x$ と置き換えると，

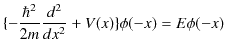
$\displaystyle \{-\dfrac{\hbar^{2}}{2m}\dfrac{d^{2}}{dx^{2}}+V(x)\}\phi(-x)=E\phi(-x)$

となり， $\phi(-x)$ も解になります．独立な解が1つの場合，解 $\phi(-x)$ は解 $\phi(x)$ の定数倍になります．つまり，

$\displaystyle \phi(-x)=c\phi(x)$

が成立します．（は定数です．）さらに， $x\to-x$ と置き換えると，

$\displaystyle \phi(x)$	$\displaystyle =c\phi(-x)$
	$\displaystyle =c\cdot c\phi(x)$
	$\displaystyle =c^{2}\phi(x)$

となります．故に，

	$\displaystyle c^{2}=1$
$% latex2html id marker 2260 $\displaystyle \therefore$$	$\displaystyle c=\pm1$

と，は特定されます．したがって，波動関数 $\phi(x)$ は偶関数，または奇関数のどちらかになります．このことを量子状態のパリティは偶または奇であるといいます．

10.6 パリティ偶の解

このSectionでは，パリティが偶の場合を取り扱います．この場合，波動関数は偶関数になります．領域はを考えれば十分です．このとき，解は次のようになります．(10.3)式と(10.12)式より，

	$\displaystyle \phi(x)=B\cos k_{x}x\,(0<x<a)$
	$\displaystyle \phi(x)=Ce^{-\alpha x}\,(x>a)$

となります．（ $\phi(x)$ は偶関数なので，としました．）これら2式をそれぞれで微分すると，

	$\displaystyle \phi'(x)=-k_{x}B\sin k_{x}x\,(0<x<a)$
	$\displaystyle \phi'(x)=-\alpha Ce^{-\alpha x}\,(x>a)$

となります．このとき，で $\phi(x)$ はなめらかに接続していなければなりません．したがって，で $\phi(x)$ が連続であるという条件より，

$\displaystyle B\cos k_{x}a=Ce^{-\alpha a}$

(10.13)

の関係が成立します．さらに，で $\phi'(x)$ が連続であるという条件より，

$\displaystyle -k_{x}B\sin k_{x}a=-\alpha Ce^{-\alpha a}$

ですから，すなわち，

$\displaystyle k_{x}B\sin k_{x}a=\alpha Ce^{-\alpha a}$

(10.14)

の関係が成立します．ここで，(10.14)式÷(10.13)式をつくると次のようになります．

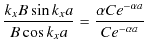	$\displaystyle \dfrac{k_{x}B\sin k_{x}a}{B\cos k_{x}a}=\dfrac{\alpha Ce^{-\alpha a}}{Ce^{-\alpha a}}$
$% latex2html id marker 2298 $\displaystyle \therefore$$	$\displaystyle k_{x}\tan k_{x}a=\alpha$

見やすくするために，

	$\displaystyle \xi\equiv k_{x}a$
	$\displaystyle \eta\equiv\alpha a$

とおくと，

$\displaystyle \eta=\xi\tan\xi$

(10.15)

が成立します．ここで，(10.8)式と(10.10)式より，

$\displaystyle \xi^{2}+\eta^{2}$	$\displaystyle =(k_{x}^{2}+\alpha^{2})a^{2}$
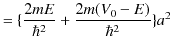	$\displaystyle =\{\dfrac{2mE}{\hbar^{2}}+\dfrac{2m(V_{0}-E)}{\hbar^{2}}\}a^{2}$

ですから，

$\displaystyle \xi^{2}+\eta^{2}=\dfrac{2mV_{0}a^{2}}{\hbar^{2}}$

(10.16)

の関係があります．(10.15)式と(10.16)式を連立すればエネルギー固有値を求めることができます．ただし，解析的な方法ではなく，グラフを使って解くことになります．このとき，エネルギー固有値は跳び跳びの値をとります．（離散エネルギー固有値になります．）

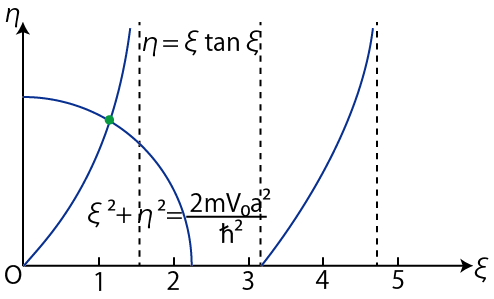
パリティ偶の解

Figure10.2: パリティ偶の解

一般に，エネルギーがポテンシャルよりも低い場合は，離散固有関数と離散エネルギー固有値が得られ，量子状態は束縛状態になります．量子はポテンシャルの井戸の底付近に局在します．

10.7 パリティ奇の解

このSectionでは，パリティが奇の場合を取り扱います．この場合，波動関数は奇関数になります．領域はを考えれば十分です．このとき，解は次のようになります．(10.3)式と(10.12)式より，

	$\displaystyle \phi(x)=A\sin k_{x}x\,(0<x<a)$
	$\displaystyle \phi(x)=Ce^{-\alpha x}\,(x>a)$

となります．（ $\phi(x)$ は奇関数なので，としました．）これら2式をそれぞれで微分すると，

	$\displaystyle \phi'(x)=k_{x}A\cos k_{x}x\,(0<x<a)$
	$\displaystyle \phi'(x)=-\alpha Ce^{-\alpha x}\,(x>a)$

となります．このとき，で $\phi(x)$ はなめらかに接続していなければなりません．したがって，で $\phi(x)$ が連続であるという条件より，

$\displaystyle A\sin k_{x}a=Ce^{-\alpha a}$

(10.17)

の関係が成立します．さらに，で $\phi'(x)$ が連続であるという条件より，

$\displaystyle k_{x}A\cos k_{x}a=-\alpha Ce^{-\alpha a}$

(10.18)

の関係が成立します．ここで，(10.18)式÷(10.17)式をつくると次のようになります．

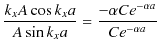	$\displaystyle \dfrac{k_{x}A\cos k_{x}a}{A\sin k_{x}a}=\dfrac{-\alpha Ce^{-\alpha a}}{Ce^{-\alpha a}}$
$% latex2html id marker 2343 $\displaystyle \therefore$$	$\displaystyle k_{x}\cot k_{x}a=-\alpha$

見やすくするために，

	$\displaystyle \xi\equiv k_{x}a$
	$\displaystyle \eta\equiv\alpha a$

とおくと，

$\displaystyle \eta=-\xi\cot\xi$

(10.19)

が成立します．ここで，前Sectionの(10.16)式，

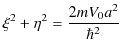
$\displaystyle \xi^{2}+\eta^{2}=\dfrac{2mV_{0}a^{2}}{\hbar^{2}}$

の関係がありました．(10.19)式と(10.16)式を連立すればエネルギー固有値を求めることができます．ただし，解析的な方法ではなく，グラフを使って解くことになります．このとき，エネルギー固有値は跳び跳びの値をとります．（離散エネルギー固有値になります．）

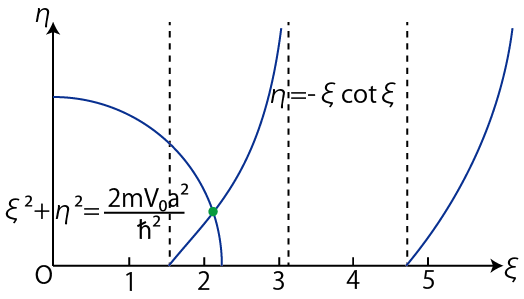
パリティ奇の解

Figure10.3: パリティ奇の解

　エネルギーの値は， $0<E<V_{0}$ の場合を考えました．このとき，古典的にはの領域で量子は存在しないはずです．しかし，上記のように波動関数 $\phi(x)$ は 0 ではなく，したがって存在確率密度 $\vert\phi(x)\vert^{2}$ も 0 ではありません．この原因は量子の波動性が現れていると考えることができます．つまり，観測する前は量子状態が確率の波として存在し，それが染み出ているという訳です．ポテンシャルの壁の外側に量子が染み出る現象をトンネル効果といいます．古典論では考えられない，波動力学特有の現象です．