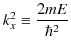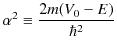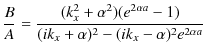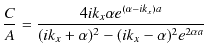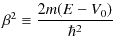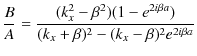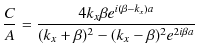Chapter11 散乱状態1(例2: ポテンシャル障壁)
11.1 1次元ポテンシャル障壁
1次元ポテンシャル障壁のポテンシャルは,図のような形をしたものです.
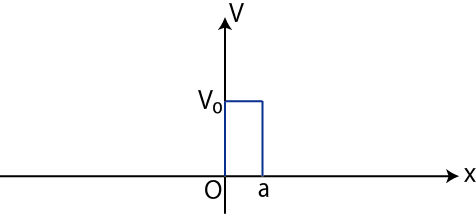
Figure11.1: ポテンシャル障壁
式で書くと,
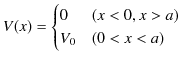
となります.ただし,![]() と
と ![]() は正の定数です.物理的な状況設定としては,
は正の定数です.物理的な状況設定としては,![]() からエネルギー
からエネルギー ![]() の量子のビームが入射され,障壁において反射または透過するようにします.なお,入射波,反射波,透過波は一定の状態に落ち着いており,定常状態になっていると考えることができます.時間に依存しないシュレディンガー方程式を用いて議論していきましょう.
の量子のビームが入射され,障壁において反射または透過するようにします.なお,入射波,反射波,透過波は一定の状態に落ち着いており,定常状態になっていると考えることができます.時間に依存しないシュレディンガー方程式を用いて議論していきましょう.
11.2 エネルギーがポテンシャルの壁よりも低い場合のシュレディンガー方程式とその解
まず,![]() の場合を考えましょう.この系について時間に依存しないシュレディンガー方程式を立てます.もとになる方程式は,
の場合を考えましょう.この系について時間に依存しないシュレディンガー方程式を立てます.もとになる方程式は,
ですが,一般に,ハミルトニアンは,
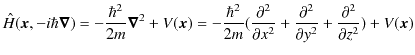
と与えられています.1次元の系を考えていますので,![]() 方向のみが関係してきます.
方向のみが関係してきます.![]() の領域においてはポテンシャルが 0 なので,シュレディンガー方程式は,
の領域においてはポテンシャルが 0 なので,シュレディンガー方程式は,
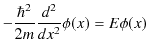
となります.これを少し変形します.
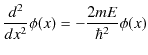
ここで,量子のエネルギー ![]() は正なので,
は正なので,
とおくと,方程式は,
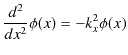
となります.この微分方程式は "束縛状態(例: 自由粒子と井戸型ポテンシャル)" のChapterで,既に解いていますが,再度見ておきます.まず,
とおき,微分方程式に代入します.(![]() と
と ![]() は複素数の定数とします.)
は複素数の定数とします.)
よって,一般解は,
となります.ただし,![]() と
と ![]() は定数です.この
は定数です.この ![]() から時間に依存する波動関数
から時間に依存する波動関数 ![]() を表すとき,
を表すとき,![]() に
に
![]() をかけることになります.("シュレディンガー方程式" のChapterでの議論を思い出して下さい.)つまり,
をかけることになります.("シュレディンガー方程式" のChapterでの議論を思い出して下さい.)つまり,
です.したがって,解の第1項は ![]() の正の方向に進行する波,つまり入射波を表し,解の第2項は
の正の方向に進行する波,つまり入射波を表し,解の第2項は ![]() の負の方向に進行する波,つまり反射波を表していることになります.
の負の方向に進行する波,つまり反射波を表していることになります.![]() の領域においては,入射波も反射波も存在しますので,解は,そのまま,
の領域においては,入射波も反射波も存在しますので,解は,そのまま,
です.(![]() と
と ![]() は定数です.)
は定数です.)![]() の領域では透過波のみが存在しますので,解は,
の領域では透過波のみが存在しますので,解は,![]() の正の方向に進行する波のみで,
の正の方向に進行する波のみで,
となります.ここで,![]() は定数です.古典的には,
は定数です.古典的には,![]() ならば,全て反射されるはずですが,量子力学の場合ははっきりとわかっていませんので,透過波が存在するものと仮定して計算していきます.透過波が存在しなければ,
ならば,全て反射されるはずですが,量子力学の場合ははっきりとわかっていませんので,透過波が存在するものと仮定して計算していきます.透過波が存在しなければ,![]() の計算結果になるはずです.次に,
の計算結果になるはずです.次に,![]() の領域を考えましょう.この領域ではポテンシャルが一定値
の領域を考えましょう.この領域ではポテンシャルが一定値 ![]() なので,シュレディンガー方程式は,
なので,シュレディンガー方程式は,
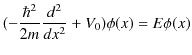
となります.これを少し変形します.
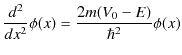
ここで,![]() の場合を考えているので,
の場合を考えているので,
とおくと,方程式は,
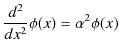
となります.この微分方程式も "束縛状態(例: 自由粒子と井戸型ポテンシャル)" のChapterで取り扱いましたが,再度見ておきます.
とおき,微分方程式に代入します.(![]() と
と ![]() は複素数の定数とします.)
は複素数の定数とします.)
よって,この方程式の一般解は,
となります.![]() と
と ![]() は定数です.
は定数です.
波動関数は,なめらかな連続関数でなければならないので,![]() と
と ![]() において,
において,![]() と
と ![]() が連続であるという境界条件を満たすことになります.境界条件を立てる前に,
が連続であるという境界条件を満たすことになります.境界条件を立てる前に,![]() を求めておきます.
を求めておきます.
それでは,境界条件を立てましょう.![]() で
で ![]() が連続であるという条件は,
が連続であるという条件は,
となります.![]() で
で ![]() が連続であるという条件は,
が連続であるという条件は,
となります.![]() で
で ![]() が連続であるという条件は,
が連続であるという条件は,
となります.![]() で
で ![]() が連続であるという条件は,
が連続であるという条件は,
となります.未知量が5つあり式が4つなので,未知量の値を求めることはできませんが,
![]() や
や
![]() といった係数の比を求めることはできます.以下,計算していきます.(11.3)式×α+(11.4)式より,
といった係数の比を求めることはできます.以下,計算していきます.(11.3)式×α+(11.4)式より,
となります.(11.3)式×α-(11.4)式より,
となります.(11.5)式×α+(11.6)式より,
となります.(11.5)式×α-(11.6)式より,
となります.上の1番目と2番目の式を,それぞれ3番目と4番目の式に代入すると,次式を得ることができます.
ここで,(11.7)式÷(11.8)式をつくり,計算していきます.
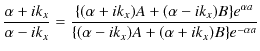 |
||
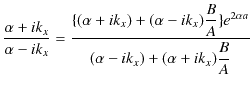 |
||
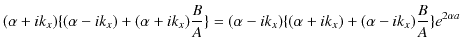 |
||
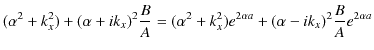 |
||
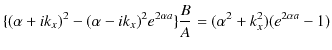 |
||
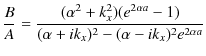 |
よって,
となります.最後の式は,反射波の複素振幅 ![]() と入射波の複素振幅
と入射波の複素振幅 ![]() の比を表しています.また,(11.7)式の両辺を
の比を表しています.また,(11.7)式の両辺を ![]() で割って計算していきます.
で割って計算していきます.
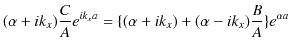
故に,
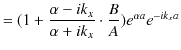 |
||
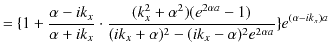 |
||
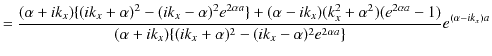 |
となります.ここで,最後の式の分子は,
です.よって,
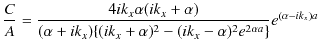
ですから,すなわち,
となります.最後の式は透過波の複素振幅 ![]() と入射波の複素振幅
と入射波の複素振幅 ![]() の比を表しています.また,
の比を表しています.また,![]() と
と ![]() は連続的に変わりますから,エネルギー固有値
は連続的に変わりますから,エネルギー固有値 ![]() も連続的に変化します.量子がポテンシャルの壁に囲まれていない場合は,量子状態は散乱状態になることがわかります.
も連続的に変化します.量子がポテンシャルの壁に囲まれていない場合は,量子状態は散乱状態になることがわかります.
11.3 エネルギーがポテンシャルの壁よりも低い場合の反射率と透過率
ここで,入射波,反射波,透過波の確率の流れ密度 ![]() を調べておきます."量子状態(波動関数と確率振幅)" のChapterで定義したように,
を調べておきます."量子状態(波動関数と確率振幅)" のChapterで定義したように,
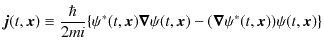
ですが,1次元の時間に依存しない場合に対して書きなおします.
ですから,
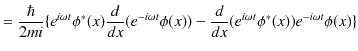 |
||
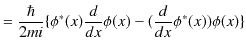 |
となります.ここで,
に対して確率の流れ密度を計算します.
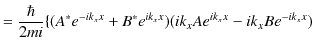 |
||
 |
||
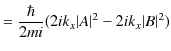 |
||
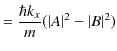 |
ここで,入射波の流れ密度 ![]() と反射波の流れ密度
と反射波の流れ密度 ![]() を次のように表すことができるでしょう.
を次のように表すことができるでしょう.
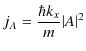 |
||
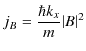 |
同様に,
に対して,確率の流れ密度を計算します.
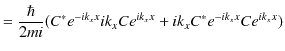 |
||
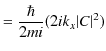 |
||
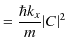 |
よって,透過波の流れ密度 ![]() を次のように表すことができるでしょう.
を次のように表すことができるでしょう.
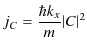
確率の流れ密度の比により,反射率と透過率を計算することができます.反射率は,
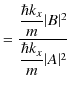 |
||
となり,透過率は,
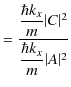 |
||
と表されます.
それでは,![]() の場合について,実際に反射率と透過率を計算してみましょう.まず,反射率を求めます.(11.9)式より,
の場合について,実際に反射率と透過率を計算してみましょう.まず,反射率を求めます.(11.9)式より,
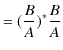 |
||
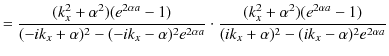 |
ですが,ここで,分母を計算します.
したがって,
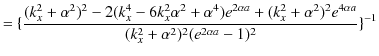 |
||
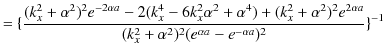 |
ですが,![]() の中の分子は,
の中の分子は,
ですから,
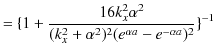 |
||
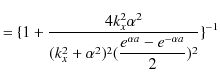 |
||
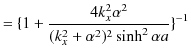 |
です.(11.1)式と(11.2)式を代入して,
![$\displaystyle =[1+\dfrac{4\dfrac{2mE}{\hbar^{2}}\dfrac{2m(V_{0}-E)}{\hbar^{2}}}...
...ac{2mE}{\hbar^{2}}+\dfrac{2m(V_{0}-E)}{\hbar^{2}}\}^{2}\sinh^{2}\alpha a}]^{-1}$](ja_Chapter11_ScatteringState1_Example2_PotentialBarrier_images/img145.png) |
||
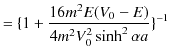 |
||
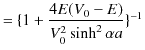 |
となります.次に透過率を計算します.(11.10)式より,
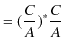 |
||
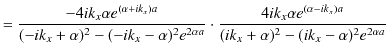 |
となります.ここで,分母は,
です.計算を続けます.
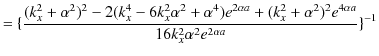 |
||
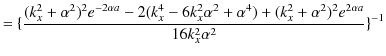 |
||
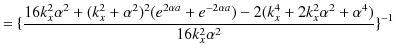 |
||
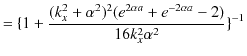 |
||
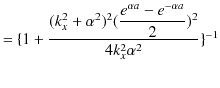 |
||
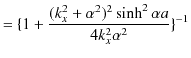 |
ここで,(11.1)式と(11.2)式を代入します.
![$\displaystyle =[1+\dfrac{\{\dfrac{2mE}{\hbar^{2}}+\dfrac{2m(V_{0}-E)}{\hbar^2}\...
...\sinh^{2}\alpha a}{4\dfrac{2mE}{\hbar^{2}}\dfrac{2m(V_{0}-E)}{\hbar^{2}}}]^{-1}$](ja_Chapter11_ScatteringState1_Example2_PotentialBarrier_images/img159.png) |
||
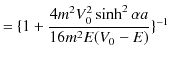 |
||
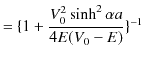 |
古典的には,![]() の場合,透過率は 0 になると思われます.しかし,上記のように波動力学による計算では,確かに透過率が存在するのです.この現象も井戸型ポテンシャルの場合と同じようにトンネル効果の現れです.量子は波動性により,ポテンシャルの壁を透過するのです.また,予想されるように,反射率と透過率を足し合わせた値は
の場合,透過率は 0 になると思われます.しかし,上記のように波動力学による計算では,確かに透過率が存在するのです.この現象も井戸型ポテンシャルの場合と同じようにトンネル効果の現れです.量子は波動性により,ポテンシャルの壁を透過するのです.また,予想されるように,反射率と透過率を足し合わせた値は ![]() になります.
になります.
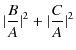 |
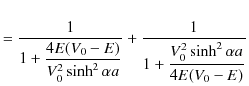 |
|
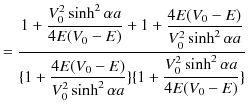 |
||
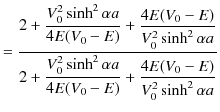 |
||
11.4 エネルギーがポテンシャルの壁よりも高い場合のシュレディンガー方程式とその解
このSectionでは,![]() の場合を考えます.
の場合を考えます.![]() の領域においてはポテンシャルが 0 なので,シュレディンガー方程式は,
の領域においてはポテンシャルが 0 なので,シュレディンガー方程式は,
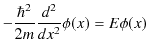
となります.これは,前々Sectionの ![]() の領域の場合と全く同じ方程式です.したがって,
の領域の場合と全く同じ方程式です.したがって,
とおくと,解は次のようになります.![]() の領域において,
の領域において,
となります.解の第1項は入射波を表し,解の第2項は反射波を表しています.![]() の解は,
の解は,
となります.次に,![]() の領域を考えましょう.シュレディンガー方程式は,
の領域を考えましょう.シュレディンガー方程式は,
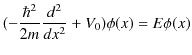
となります.これを少し変形します.
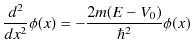
ここで,![]() の場合を考えているので,
の場合を考えているので,
とおくと,方程式は,
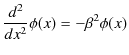
となります.右辺の符号が負ですから,上と同様に,この方程式の一般解は,
となります.ただし,![]() と
と ![]() は定数です.
は定数です.
ここで,![]() と
と ![]() において,
において,![]() と
と ![]() が連続であるという境界条件を満たさなければなりません.境界条件を立てる前に,
が連続であるという境界条件を満たさなければなりません.境界条件を立てる前に,![]() を求めておきます.
を求めておきます.
それでは,境界条件を立てましょう.![]() で
で ![]() が連続であるという条件は,
が連続であるという条件は,
となります.![]() で
で ![]() が連続であるという条件は,
が連続であるという条件は,
となります.![]() で
で ![]() が連続であるという条件は,
が連続であるという条件は,
となります.![]() で
で ![]() が連続であるという条件は,
が連続であるという条件は,
となります.未知量が5つあり式が4つなので,未知量の値を求めることはできませんが,
![]() や
や
![]() といった係数の比を求めることはできます.以下,計算していきます.(11.13)式×β+(11.14)式より,
といった係数の比を求めることはできます.以下,計算していきます.(11.13)式×β+(11.14)式より,
となります.(11.13)式×β-(11.14)式より,
となります.(11.15)式×β+(11.16)式より,
となります.(11.15)式×β-(11.16)式より,
となります.上の1番目と2番目の式を,それぞれ3番目と4番目の式に代入すると,次式を得ることができます.
ここで,(11.17)式÷(11.18)式をつくり,計算していきます.
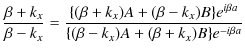 |
||
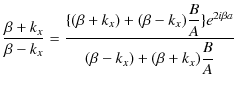 |
||
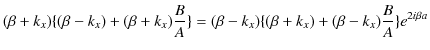 |
||
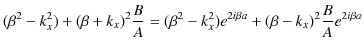 |
||
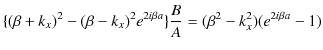 |
||
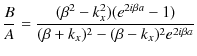 |
よって,
です.最後の式は,反射波の複素振幅 ![]() と入射波の複素振幅
と入射波の複素振幅 ![]() の比を表しています.また,(11.17)式の両辺を
の比を表しています.また,(11.17)式の両辺を ![]() で割って計算していきます.
で割って計算していきます.
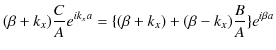
よって,
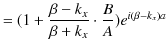 |
||
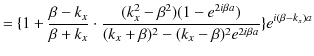 |
||
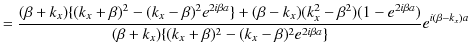 |
ですが,分子は,
です.故に,
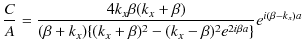
ですから,よって,
となります.最後の式は透過波の複素振幅 ![]() と入射波の複素振幅
と入射波の複素振幅 ![]() の比を表しています.また,
の比を表しています.また,![]() と
と ![]() は連続的に変わりますから,エネルギー固有値
は連続的に変わりますから,エネルギー固有値 ![]() も連続的に変化します.量子がポテンシャルの壁に囲まれていない場合は,量子状態は散乱状態になることがわかります.
も連続的に変化します.量子がポテンシャルの壁に囲まれていない場合は,量子状態は散乱状態になることがわかります.
11.5 エネルギーがポテンシャルの壁よりも高い場合の反射率と透過率
それでは,![]() の場合について,反射率と透過率を計算してみましょう.
の場合について,反射率と透過率を計算してみましょう.![]() と
と ![]() での確率の流れ密度の式は前と同じになりますので,この場合も反射率は
での確率の流れ密度の式は前と同じになりますので,この場合も反射率は
![]() で,透過率は
で,透過率は
![]() になります.まず,反射率を求めます.(11.19)式より,
になります.まず,反射率を求めます.(11.19)式より,
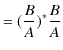 |
||
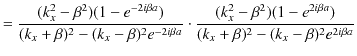 |
ですが,ここで,分母は,
です.故に,
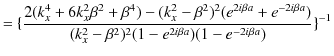 |
||
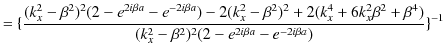 |
||
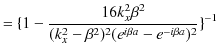 |
||
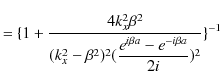 |
||
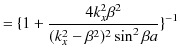 |
です.ここで,(11.11)式と(11.12)式より,
![$\displaystyle =[1+\dfrac{4\dfrac{2mE}{\hbar^{2}}\dfrac{2m(E-V_{0})}{\hbar^{2}}}...
...frac{2mE}{\hbar^{2}}-\dfrac{2m(E-V_{0})}{\hbar^{2}}\}^{2}\sin^{2}\beta a}]^{-1}$](ja_Chapter11_ScatteringState1_Example2_PotentialBarrier_images/img219.png) |
||
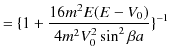 |
||
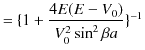 |
となります.![]() の場合,古典的には反射率は 0 ですが,量子力学ではこのように有限値をとります.ここでも量子の波動性が効いていますね.次に透過率を計算します.(11.20)式より,
の場合,古典的には反射率は 0 ですが,量子力学ではこのように有限値をとります.ここでも量子の波動性が効いていますね.次に透過率を計算します.(11.20)式より,
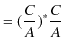 |
||
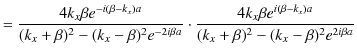 |
ですが,ここで,分母は,
となります.故に,
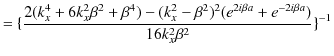 |
||
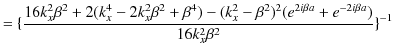 |
||
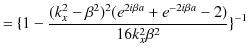 |
||
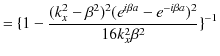 |
||
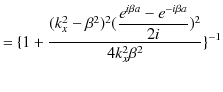 |
||
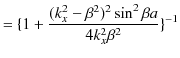 |
です.ここで,(11.11)式と(11.12)式を代入して,
![$\displaystyle =[1+\dfrac{\{\dfrac{2mE}{\hbar^{2}}-\dfrac{2m(E-V_{0})}{\hbar^{2}...
...2}\sin^{2}\beta a}{4\dfrac{2mE}{\hbar^{2}}\dfrac{2m(E-V_{0})}{\hbar^{2}}}]^{-1}$](ja_Chapter11_ScatteringState1_Example2_PotentialBarrier_images/img229.png) |
||
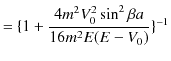 |
||
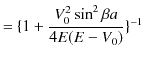 |
となります.予想されるように,反射率と透過率を足し合わせた値は ![]() になることを確認しておきましょう.
になることを確認しておきましょう.
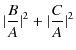 |
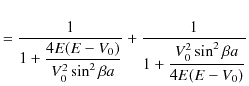 |
|
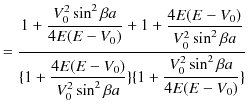 |
||
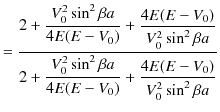 |
||