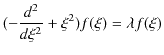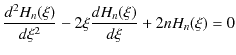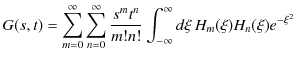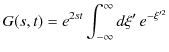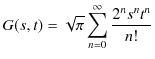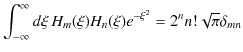J Simplicity 束縛状態2（例3: 調和振動子）

Chapter12 束縛状態2（例3: 調和振動子）

12.1 1次元調和振動子のシュレディンガー方程式

古典的には調和振動子とは，ばね振り子や単振り子のような系でした．そして，全ての任意の振動はフーリエ解析により，調和振動子に分解できるという強力な性質をもっています．その調和振動子を波動力学的に取り扱ってみましょう．簡単のため，空間は1次元にします．時間に依存しないシュレディンガー方程式を立ててみます．もとになる方程式は，

$\displaystyle \hat{H}(\bm{x},-i\hbar\bm{\nabla})\phi(\bm{x})=E\phi(\bm{x})$

ですが，一般に，ハミルトニアンは，

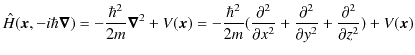
$\displaystyle \hat{H}(\bm{x},-i\hbar\bm{\nabla})=-\dfrac{\hbar^{2}}{2m}\bm{\nab... ...c{\partial^{2}}{\partial y^{2}}+\dfrac{\partial^{2}}{\partial z^{2}})+V(\bm{x})$

と与えられています．1次元の系を考えていますので，方向のみが関係してきます．また，古典論における1次元調和振動子のポテンシャルは，

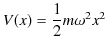
$\displaystyle V(x)=\dfrac{1}{2}m\omega^{2}x^{2}$

と表すことができます．ただし，は質量， $\omega$ は角振動数です．（振動の中心を原点にとっています．）座標演算子は， $\hat{x}=x$ であり，古典的な量と変わりませんから，このポテンシャルは量子化しても，同じ式で表せます．故に，シュレディンガー方程式は，

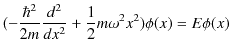
$\displaystyle (-\dfrac{\hbar^{2}}{2m}\dfrac{d^{2}}{dx^{2}}+\dfrac{1}{2}m\omega^{2}x^{2})\phi(x)=E\phi(x)$

となります．この方程式を解きやすくするために，

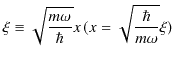	$\displaystyle \xi\equiv\sqrt{\dfrac{m\omega}{\hbar}}x\,(x=\sqrt{\dfrac{\hbar}{m\omega}}\xi)$
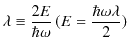	$\displaystyle \lambda\equiv\dfrac{2E}{\hbar\omega}\,(E=\dfrac{\hbar\omega\lambda}{2})$
	$\displaystyle f(\xi)=\phi(x)$

という変数の変換をします．このとき，

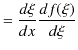$\displaystyle \dfrac{d\phi(x)}{dx}$	$\displaystyle =\dfrac{d\xi}{dx}\dfrac{df(\xi)}{d\xi}$
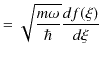	$\displaystyle =\sqrt{\dfrac{m\omega}{\hbar}}\dfrac{df(\xi)}{d\xi}$

ですから，

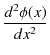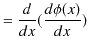$\displaystyle \dfrac{d^{2}\phi(x)}{dx^{2}}$	$\displaystyle =\dfrac{d}{dx}(\dfrac{d\phi(x)}{dx})$
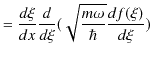	$\displaystyle =\dfrac{d\xi}{dx}\dfrac{d}{d\xi}(\sqrt{\dfrac{m\omega}{\hbar}}\dfrac{df(\xi)}{d\xi})$
	$\displaystyle =\sqrt{\dfrac{m\omega}{\hbar}}\dfrac{d}{d\xi}(\sqrt{\dfrac{m\omega}{\hbar}}\dfrac{df(\xi)}{d\xi})$
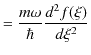	$\displaystyle =\dfrac{m\omega}{\hbar}\dfrac{d^{2}f(\xi)}{d\xi^{2}}$

となります．新しい変数でシュレディンガー方程式を書きなおしていくと，次のようになります．

	$\displaystyle (-\dfrac{\hbar^{2}}{2m}\dfrac{m\omega}{\hbar}\dfrac{d^{2}}{d\xi^{... ...ega^{2}\dfrac{\hbar}{m\omega}\xi^{2})f(\xi)=\dfrac{\hbar\omega\lambda}{2}f(\xi)$
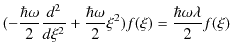$% latex2html id marker 2532 $\displaystyle \therefore$$	$\displaystyle (-\dfrac{\hbar\omega}{2}\dfrac{d^{2}}{d\xi^{2}}+\dfrac{\hbar\omega}{2}\xi^{2})f(\xi)=\dfrac{\hbar\omega\lambda}{2}f(\xi)$

したがって，

$\displaystyle (-\dfrac{d^{2}}{d\xi^{2}}+\xi^{2})f(\xi)=\lambda f(\xi)$

(12.1)

となります．(12.1)式は常微分方程式の固有値方程式です．次のSection以降で解いていきましょう．

12.2 エルミート多項式による解法

このSectionでは，(12.1)式をエルミート多項式と呼ばれるものを使って解くことを試みます． $\xi\to\pm\infty$ の極限を考えると， $\xi\gg\lambda$ なので，方程式は，

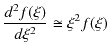
$\displaystyle \dfrac{d^{2}f(\xi)}{d\xi^{2}}\cong\xi^{2}f(\xi)$

と近似されます．この式の漸近解は，

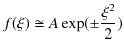
$\displaystyle f(\xi)\cong A\exp(\pm\dfrac{\xi^{2}}{2})$

です．（ただし，は定数です．）実際，

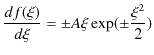	$\displaystyle \dfrac{df(\xi)}{d\xi}=\pm A\xi\exp(\pm\dfrac{\xi^{2}}{2})$
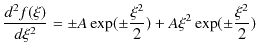$% latex2html id marker 2548 $\displaystyle \therefore$$	$\displaystyle \dfrac{d^{2}f(\xi)}{d\xi^{2}}=\pm A\exp(\pm\dfrac{\xi^{2}}{2})+A\xi^{2}\exp(\pm\dfrac{\xi^{2}}{2})$

となり， $\xi\to\pm\infty$ の極限で，解になっていることがわかります．ここで，指数関数の肩で正の符号をとると， $\xi\to\pm\infty$ で $f(\xi)$ は発散してしまい，量子の存在確率が無限大になってしまいます．そこで，指数関数の肩の符号は負であると決定されます．

　この漸近解をもとに，方程式の一般解を求めましょう．そのために， $\xi$ の関数 $u(\xi)$ を導入して，

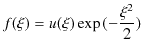
$\displaystyle f(\xi)=u(\xi)\exp⁡(-\dfrac{\xi^{2}}{2})$

とおきます．ここで， $f(\xi)$ を $\xi$ で微分していくと，次のようになります．

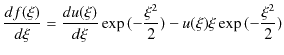	$\displaystyle \dfrac{df(\xi)}{d\xi}=\dfrac{du(\xi)}{d\xi}\exp⁡(-\dfrac{\xi^{2}}{2})-u(\xi)\xi\exp⁡(-\dfrac{\xi^{2}}{2})$
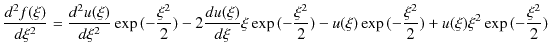$% latex2html id marker 2567 $\displaystyle \therefore$$	$\displaystyle \dfrac{d^{2}{f(\xi)}}{d\xi^{2}}=\dfrac{d^{2}u(\xi)}{d\xi^{2}}\exp... ...})-u(\xi)\exp⁡(-\dfrac{\xi^{2}}{2})+u(\xi)\xi^{2}\exp⁡(-\dfrac{\xi^{2}}{2})$

このとき，(12.1)式は，

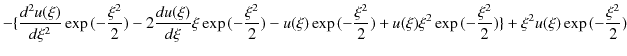	$\displaystyle -\{\dfrac{d^{2}u(\xi)}{d\xi^{2}}\exp⁡(-\dfrac{\xi^{2}}{2})-2\df... ...\xi^{2}\exp⁡(-\dfrac{\xi^{2}}{2})\}+\xi^{2}u(\xi)\exp⁡(-\dfrac{\xi^{2}}{2})$
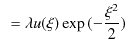	$\displaystyle \,\,\,=\lambda u(\xi)\exp⁡(-\dfrac{\xi^{2}}{2})$

すなわち，

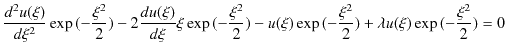
$\displaystyle \dfrac{d^{2}u(\xi)}{d\xi^{2}}\exp⁡(-\dfrac{\xi^{2}}{2})-2\dfrac... ...u(\xi)\exp⁡(-\dfrac{\xi^{2}}{2})+\lambda u(\xi)\exp⁡(-\dfrac{\xi^{2}}{2})=0$

ですから，

$\displaystyle \dfrac{d^{2}u(\xi)}{d\xi^{2}}-2\xi\dfrac{du(\xi)}{d\xi}+(\lambda-1)u(\xi)=0$

(12.2)

となります．(12.2)式を解くために， $u(\xi)$ は $\xi$ のべき級数で展開できると仮定します．すなわち，

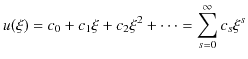
$\displaystyle u(\xi)=c_{0}+c_{1}\xi+c_{2}\xi^{2}+\cdots=\sum_{s=0}^{\infty}c_{s}\xi^{s}$

とします．（ $c_{s}$ は展開係数です．）ここで， $u(\xi)$ を $\xi$ で微分していきます．

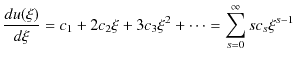	$\displaystyle \dfrac{du(\xi)}{d\xi}=c_{1}+2c_{2}\xi+3c_{3}\xi^{2}+\cdots=\sum_{s=0}^{\infty}sc_{s}\xi^{s-1}$
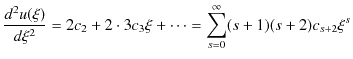$% latex2html id marker 2588 $\displaystyle \therefore$$	$\displaystyle \dfrac{d^{2}u(\xi)}{d\xi^{2}}=2c_{2}+2\cdot3c_{3}\xi+\cdots=\sum_{s=0}^{\infty}(s+1)(s+2)c_{s+2}\xi^{s}$

これらの式を，(12.2)式に代入して計算します．

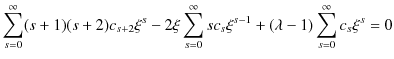	$\displaystyle \sum_{s=0}^{\infty}(s+1)(s+2)c_{s+2}\xi^{s}-2\xi\sum_{s=0}^{\infty}sc_{s}\xi^{s-1}+(\lambda-1)\sum_{s=0}^{\infty}c_{s}\xi^{s}=0$
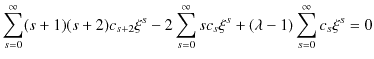$% latex2html id marker 2591 $\displaystyle \therefore$$	$\displaystyle \sum_{s=0}^{\infty}(s+1)(s+2)c_{s+2}\xi^{s}-2\sum_{s=0}^{\infty}sc_{s}\xi^{s}+(\lambda-1)\sum_{s=0}^{\infty}c_{s}\xi^{s}=0$
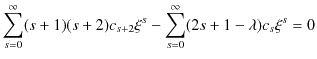$% latex2html id marker 2593 $\displaystyle \therefore$$	$\displaystyle \sum_{s=0}^{\infty}(s+1)(s+2)c_{s+2}\xi^{s}-\sum_{s=0}^{\infty}(2s+1-\lambda)c_{s}\xi^{s}=0$

最後の式が成立するためには， $\xi^{s}$ の係数は全て 0 にならなければなりません．したがって，

$\displaystyle (s+1)(s+2)c_{s+2}=(2s+1-\lambda)c_{s}$

(12.3)

が成り立ちます．

　ここで，1次元調和振動子のポテンシャルが偶関数であることに注意しましょう．このとき，"束縛状態（例: 自由粒子と井戸型ポテンシャル）" のChapterでのパリティについての議論により，波動関数 $\phi(x)$ は偶関数または奇関数であることがわかります．すなわち， $f(\xi)$ が偶関数または奇関数なので，結局 $u(\xi)$ が偶関数または奇関数ということになります．よって， $u(\xi)$ は $\xi$ について，偶べきのみか，または奇べきのみの級数になります．よく知られているように，この級数が無限級数の場合，波動関数 $\phi(x)$ が発散することを証明しましょう．まず，(12.3)式より，

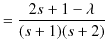$\displaystyle \dfrac{c_{s+2}}{c_{s}}$	$\displaystyle =\dfrac{2s+1-\lambda}{(s+1)(s+2)}$
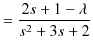	$\displaystyle =\dfrac{2s+1-\lambda}{s^{2}+3s+2}$
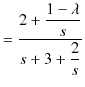	$\displaystyle =\dfrac{2+\dfrac{1-\lambda}{s}}{s+3+\dfrac{2}{s}}$

となりますが， $s\to\infty$ のとき，

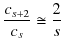
$\displaystyle \dfrac{c_{s+2}}{c_{s}}\cong\dfrac{2}{s}$

と近似されます．この係数の関係は，関数，

$\displaystyle g(\xi^{2})=e^{\xi^{2}}$

と同じであることが，次のように確かめられます． $\eta\equiv\xi^{2}$ とおき， $g(\xi^{2})=g(\eta)=e^{\eta}$ をマクローリン展開すると，

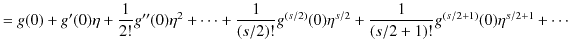$\displaystyle g(\eta)$	$\displaystyle =g(0)+g'(0)\eta+\dfrac{1}{2!}g''(0)\eta^{2}+\cdots+\dfrac{1}{(s/2)!}g^{(s/2)}(0)\eta^{s/2}+\dfrac{1}{(s/2+1)!}g^{(s/2+1)}(0)\eta^{s/2+1}+\cdots$
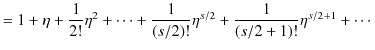	$\displaystyle =1+\eta+\dfrac{1}{2!}\eta^{2}+\cdots+\dfrac{1}{(s/2)!}\eta^{s/2}+\dfrac{1}{(s/2+1)!}\eta^{s/2+1}+\cdots$
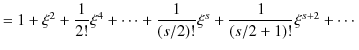	$\displaystyle =1+\xi^{2}+\dfrac{1}{2!}\xi^{4}+\cdots+\dfrac{1}{(s/2)!}\xi^{s}+\dfrac{1}{(s/2+1)!}\xi^{s+2}+\cdots$

となります． $\xi^{s+2}$ の係数 $d_{s+2}$ と $\xi^{s}$ の係数 $d_{s}$ の比を計算します．

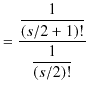$\displaystyle \dfrac{d_{s+2}}{d_{s}}$	$\displaystyle =\dfrac{\dfrac{1}{(s/2+1)!}}{\dfrac{1}{(s/2)!}}$
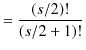	$\displaystyle =\dfrac{(s/2)!}{(s/2+1)!}$
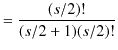	$\displaystyle =\dfrac{(s/2)!}{(s/2+1)(s/2)!}$
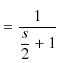	$\displaystyle =\dfrac{1}{\dfrac{s}{2}+1}$
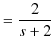	$\displaystyle =\dfrac{2}{s+2}$

ここで， $s\to\infty$ のとき，

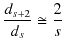
$\displaystyle \dfrac{d_{s+2}}{d_{s}}\cong\dfrac{2}{s}$

と近似されます．確かに， $c_{s}$ についての関係と同じになりますね．よって，べき級数が無限級数ならば， $\xi$ が大きいときの $u(\xi)$ の振る舞いは，

$\displaystyle u(\xi)\varpropto e^{\xi^{2}}$

となることがわかります．このとき，波動関数 $\phi(x)$ は，

$\displaystyle \phi(x)$	$\displaystyle =f(\xi)$
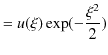	$\displaystyle =u(\xi)\exp(-\dfrac{\xi^{2}}{2})$
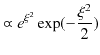	$\displaystyle \varpropto e^{\xi^{2}}\exp(-\dfrac{\xi^{2}}{2})$
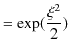	$\displaystyle =\exp(\dfrac{\xi^{2}}{2})$

となります．この波動関数は $\xi$ が大きいとき，すなわちが大きいとき，発散してしまいますね．これが証明したかったことです．一方，古典的な1次元調和振動子は原点付近で振動を続けますが，波動力学的な系においても，波動関数は原点付近に局在することが考えられます．つまり， $x\to\pm\infty\,(\xi\to\pm\infty)$ において， $\phi(x)$ が 0 にならなければなりません．そのためには，べき級数が無限級数ではなく，有限でなければならないのです． $u(\xi)$ は偶べきのみ，または奇べきのみの級数だったことは，先ほど説明しましたが，その級数が有限であるためには，(12.3)式より，

$\displaystyle \lambda=2n+1\,(n=0,1,2,\cdots)$

の関係が満たされていることが，条件になります．このとき，級数の途中から，

$\displaystyle c_{n+2},c_{n+4},c_{n+6},\cdots$

は，全て 0 になります．

　ここで，エネルギー固有値 $E_{n}$ を求めます．

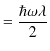$\displaystyle E$	$\displaystyle =\dfrac{\hbar\omega\lambda}{2}$
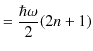	$\displaystyle =\dfrac{\hbar\omega}{2}(2n+1)$

ですから，

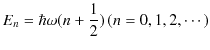
$\displaystyle E_{n}=\hbar\omega(n+\dfrac{1}{2})\,(n=0,1,2,\cdots)$

となります．ポテンシャルの中でのエネルギー固有値を図で示しておきます．エネルギー固有値は離散的な値をもつことが理解できます．また，量子は束縛状態にあることも確認できます．

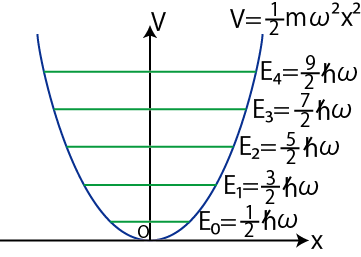
調和振動子

Figure12.1: 調和振動子

量子数が増えるに従って，エネルギーは増大していきます．の状態を基底状態，が2以上の状態を励起状態といいます．のとき，エネルギーが最小値をとり，絶対零度の状態になります．古典的にはエネルギーは 0 になるはずですが，この場合も量子は零点振動をしています．波動力学では不確定性原理のため，量子は静止することができないのです．

　次に，(12.2)式，

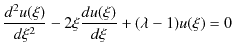
$\displaystyle \dfrac{d^{2}u(\xi)}{d\xi^{2}}-2\xi\dfrac{du(\xi)}{d\xi}+(\lambda-1)u(\xi)=0$

の解を求めましょう．この式に，

$\displaystyle \lambda=2n+1\,(n=0,1,2,\cdots)$

を代入すると，

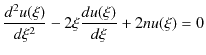
$\displaystyle \dfrac{d^{2}u(\xi)}{d\xi^{2}}-2\xi\dfrac{du(\xi)}{d\xi}+2nu(\xi)=0$

となります．この方程式と同形の，

$\displaystyle \dfrac{d^{2}H_{n}(\xi)}{d\xi^{2}}-2\xi\dfrac{dH_{n}(\xi)}{d\xi}+2nH_{n}(\xi)=0$

(12.4)

の微分方程式を満たす， $\xi$ の次の多項式 $H_{n}(\xi)$ をエルミート多項式といいます． $u(\xi)$ は $H_{n}(\xi)$ で表されます．エルミート多項式は母関数，

$\displaystyle S(\xi,t)=e^{-t^{2}+2\xi t}$

を用いて定義することができます．その方法は，母関数を展開して，

$\displaystyle S(\xi,t)$	$\displaystyle =e^{-t^{2}+2\xi t}$
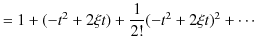	$\displaystyle =1+(-t^{2}+2\xi t)+\dfrac{1}{2!}(-t^{2}+2\xi t)^{2}+\cdots$
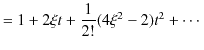	$\displaystyle =1+2\xi t+\dfrac{1}{2!}(4\xi^{2}-2)t^{2}+\cdots$

としておいて，

$\displaystyle S(\xi,t)=e^{-t^{2}+2\xi t}=\sum_{n=0}^{\infty}\dfrac{H_{n}(\xi)}{n!}t^{n}$

(12.5)

によって，エルミート多項式 $H_{n}(\xi)$ を定義するのです．このとき，具体的には，

$\displaystyle H_{0}(\xi)$	$\displaystyle =1$
$\displaystyle H_{1}(\xi)$	$\displaystyle =2\xi$
$\displaystyle H_{2}(\xi)$	$\displaystyle =4\xi^{2}-2$
	$\displaystyle \vdots$

のようになります．それでは，この母関数を用いた定義，(12.5)式による $H_{n}(\xi)$ が確かに，(12.4)式の微分方程式の解になっていることを示しておきます．(12.5)式を $\xi$ で偏微分すると，左辺は，

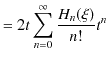$\displaystyle 2t\cdot e^{-t^{2}+2\xi t}$	$\displaystyle =2t\sum_{n=0}^{\infty}\dfrac{H_{n}(\xi)}{n!}t^{n}$
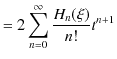	$\displaystyle =2\sum_{n=0}^{\infty}\dfrac{H_{n}(\xi)}{n!}t^{n+1}$

となります．右辺も $\xi$ で偏微分します．

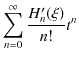
$\displaystyle \sum_{n=0}^{\infty}\dfrac{H'_{n}(\xi)}{n!}t^{n}$

故に，

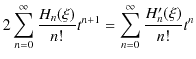
$\displaystyle 2\sum_{n=0}^{\infty}\dfrac{H_{n}(\xi)}{n!}t^{n+1}=\sum_{n=0}^{\infty}\dfrac{H'_{n}(\xi)}{n!}t^{n}$

となります．この式の両辺の $t^{n}$ の係数を比較して，

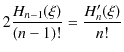
$\displaystyle 2\dfrac{H_{n-1}(\xi)}{(n-1)!}=\dfrac{H'_{n}(\xi)}{n!}$

すなわち，

$\displaystyle H'_{n}(\xi)=2nH_{n-1}(\xi)$

(12.6)

の関係式を得ることができます．また，(12.5)式を，で偏微分します．左辺は，

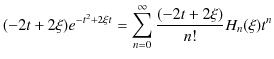
$\displaystyle (-2t+2\xi)e^{-t^{2}+2\xi t}=\sum_{n=0}^{\infty}\dfrac{(-2t+2\xi)}{n!}H_{n}(\xi)t^{n}$

となります．このとき，右辺もで偏微分すると，

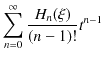
$\displaystyle \sum_{n=0}^{\infty}\dfrac{H_{n}(\xi)}{(n-1)!}t^{n-1}$

となります．したがって，

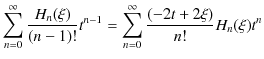
$\displaystyle \sum_{n=0}^{\infty}\dfrac{H_{n}(\xi)}{(n-1)!}t^{n-1}=\sum_{n=0}^{\infty}\dfrac{(-2t+2\xi)}{n!}H_{n}(\xi)t^{n}$

という等式が成立します．ここで， $t^{n}$ の係数を比較して，

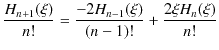
$\displaystyle \dfrac{H_{n+1}(\xi)}{n!}=\dfrac{-2H_{n-1}(\xi)}{(n-1)!}+\dfrac{2\xi H_{n}(\xi)}{n!}$

となります．よって，

$\displaystyle H_{n+1}(\xi)=2\xi H_{n}(\xi)-2nH_{n-1}(\xi)$

(12.7)

の関係式が成立します．この式を $\xi$ で微分します．

$\displaystyle H'_{n+1}(\xi)=2H_{n}(\xi)+2\xi H'_{n}(\xi)-2nH'_{n-1}(\xi)$

ここで，関係式(12.6)式を使い，計算していきます．

	$\displaystyle 2(n+1)H_{n}(\xi)=2H_{n}(\xi)+2\xi H'_{n}(\xi)-H''_{n}(\xi)$
$% latex2html id marker 2774 $\displaystyle \therefore$$	$\displaystyle H''_{n}(\xi)-2\xi H'_{n}(\xi)+2nH_{n}(\xi)=0$

最後の式より，母関数(12.5)式により定義されたエルミート多項式 $H_{n}(\xi)$ が，エルミートの微分方程式(12.4)式を満たすことが確認されました．

　これまでの議論により，1次元調和振動子の番目の固有関数は，

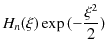
$\displaystyle H_{n}(\xi)\exp⁡(-\dfrac{\xi^{2}}{2})$

に比例することが理解されますが，この関数を規格化しましょう．そのために，次の積分を考えます．

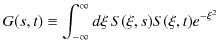
$\displaystyle G(s,t)\equiv\int_{-\infty}^{\infty}d\xi\,S(\xi,s)S(\xi,t)e^{-\xi^{2}}$

ここで，この積分に母関数を表す(12.5)式，

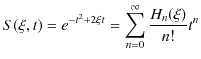
$\displaystyle S(\xi,t)=e^{-t^{2}+2\xi t}=\sum_{n=0}^{\infty}\dfrac{H_{n}(\xi)}{n!}t^{n}$

の右辺を代入します．

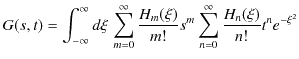
$\displaystyle G(s,t)=\int_{-\infty}^{\infty}d\xi\,\sum_{m=0}^{\infty}\dfrac{H_{m}(\xi)}{m!}s^{m}\sum_{n=0}^{\infty}\dfrac{H_{n}(\xi)}{n!}t^{n}e^{-\xi^{2}}$

したがって，

$\displaystyle G(s,t)=\sum_{m=0}^{\infty}\sum_{n=0}^{\infty}\dfrac{s^{m}t^{n}}{m!n!}\int_{-\infty}^{\infty}d\xi\,H_{m}(\xi)H_{n}(\xi)e^{-\xi^{2}}$

(12.8)

となります．一方，積分に(12.5)式の左辺を代入して計算します．

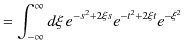$\displaystyle G(s,t)$	$\displaystyle =\int_{-\infty}^{\infty}d\xi\,e^{-s^{2}+2\xi s}e^{-t^{2}+2\xi t}e^{-\xi^{2}}$
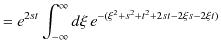	$\displaystyle =e^{2st}\int_{-\infty}^{\infty}d\xi\,e^{-(\xi^{2}+s^{2}+t^{2}+2st-2\xi s-2\xi t)}$
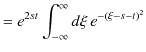	$\displaystyle =e^{2st}\int_{-\infty}^{\infty}d\xi\,e^{-(\xi-s-t)^{2}}$

ここで，

$\displaystyle \xi'\equiv\xi-s-t$

と置き換えます．このとき，

$\displaystyle G(s,t)=e^{2st}\int_{-\infty}^{\infty}d\xi'\,e^{-\xi'^{2}}$

(12.9)

となります．

　ここで，ガウス積分の公式，

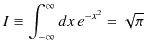
$\displaystyle I\equiv\int_{-\infty}^{\infty}dx\,e^{-x^{2}}=\sqrt{\pi}$

の導出をしておきましょう．

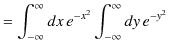$\displaystyle I^{2}$	$\displaystyle =\int_{-\infty}^{\infty}dx\,e^{-x^{2}}\int_{-\infty}^{\infty}dy\,e^{-y^{2}}$
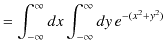	$\displaystyle =\int_{-\infty}^{\infty}dx\int_{-\infty}^{\infty}dy\,e^{-(x^{2}+y^{2})}$

ですが，ここで，2次元極座標 $(r,\theta)$ を導入します．は，

	$\displaystyle x=r\cos\theta$
	$\displaystyle y=r\sin\theta$

の式で， $(r,\theta)$ へ変数変換されます．

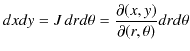
$\displaystyle dxdy=J\,drd\theta=\dfrac{\partial(x,y)}{\partial(r,\theta)}drd\theta$

の関係がありますが，この式の中で，ヤコビアンは，

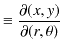$\displaystyle J$	$\displaystyle \equiv\dfrac{\partial(x,y)}{\partial(r,\theta)}$
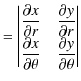	$\displaystyle = \begin{vmatrix} \dfrac{\partial x}{\partial r}&\dfrac{\partia... ...c{\partial x}{\partial\theta}&\dfrac{\partial y}{\partial\theta} \end{vmatrix}$
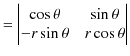	$\displaystyle = \begin{vmatrix} \cos\theta&\sin\theta\\ -r\sin\theta&r\cos\theta \end{vmatrix}$
	$\displaystyle =r\cos^{2}\theta+r\sin^{2}\theta$
	$\displaystyle =r$

と計算されます．また，

$\displaystyle x^{2}+y^{2}$	$\displaystyle =(r\cos\theta)^{2}+(r\sin\theta)^{2}$
	$\displaystyle =r^{2}$

です．積分範囲は2次元平面，全てを覆いますので，は 0 から $\infty$ まで， $\theta$ は 0 から $2\pi$ までです．故に， $I^{2}$ は，

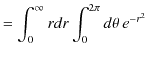$\displaystyle I^{2}$	$\displaystyle =\int_{0}^{\infty}rdr\int_{0}^{2\pi}d\theta\,e^{-r^{2}}$
	$\displaystyle =2\pi[-\dfrac{1}{2}e^{-r^{2}}]_{0}^{\infty}$
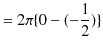	$\displaystyle =2\pi\{0-(-\dfrac{1}{2})\}$
	$\displaystyle =\pi$

となります．したがって，

$\displaystyle I=\sqrt{\pi}$

が導かれます．

　このガウス積分の公式を使って，(12.9)式は，

$\displaystyle G(s,t)=\sqrt{\pi}e^{2st}$

となります．さらに，指数関数を展開して，

$\displaystyle G(s,t)=\sqrt{\pi}\sum_{n=0}^{\infty}\dfrac{2^{n}s^{n}t^{n}}{n!}$

(12.10)

と表されます．以上，に対する2つの表式，(12.8)式と(12.10)式をイコールで結びます．

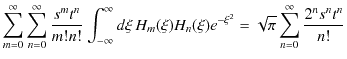
$\displaystyle \sum_{m=0}^{\infty}\sum_{n=0}^{\infty}\dfrac{s^{m}t^{n}}{m!n!}\in... ...H_{n}(\xi)e^{-\xi^{2}}=\sqrt{\pi}\sum_{n=0}^{\infty}\dfrac{2^{n}s^{n}t^{n}}{n!}$

$s^{m}t^{n}$ の係数を比較すると，右辺ではの項だけあらわれることに注意しましょう．したがって， $m\neq n$ の場合は，

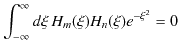
$\displaystyle \int_{-\infty}^{\infty}d\xi\,H_{m}(\xi)H_{n}(\xi)e^{-\xi^{2}}=0$

となり，の場合は，

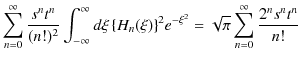	$\displaystyle \sum_{n=0}^{\infty}\dfrac{s^{n}t^{n}}{(n!)^{2}}\int_{-\infty}^{\i... ...\xi)\}^{2}e^{-\xi^{2}}=\sqrt{\pi}\sum_{n=0}^{\infty}\dfrac{2^{n}s^{n}t^{n}}{n!}$
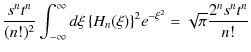$% latex2html id marker 2866 $\displaystyle \therefore$$	$\displaystyle \dfrac{s^{n}t^{n}}{(n!)^{2}}\int_{-\infty}^{\infty}d\xi\,\{H_{n}(\xi)\}^{2}e^{-\xi^{2}}=\sqrt{\pi}\dfrac{2^{n}s^{n}t^{n}}{n!}$
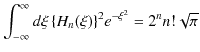$% latex2html id marker 2868 $\displaystyle \therefore$$	$\displaystyle \int_{-\infty}^{\infty}d\xi\,\{H_{n}(\xi)\}^{2}e^{-\xi^{2}}=2^{n}n!\sqrt{\pi}$

となります．まとめて表すと，

$\displaystyle \int_{-\infty}^{\infty}d\xi\,H_{m}(\xi)H_{n}(\xi)e^{-\xi^{2}}=2^{n}n!\sqrt{\pi}\delta_{mn}$

(12.11)

が成立します．ただし，右辺の最後の記号は，クロネッカーのデルタで，次の式で定義されます．

$\displaystyle \delta_{mn}\equiv\begin{cases} 1 & (m=n)\\ 0 & (m\neq n) \end{cases}$

(12.11)式を使って，1次元調和振動子の固有関数，

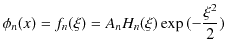
$\displaystyle \phi_{n}(x)=f_{n}(\xi)=A_{n}H_{n}(\xi)\exp⁡(-\dfrac{\xi^{2}}{2})$

を規格化します．（ただし，

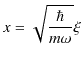
$\displaystyle x=\sqrt{\dfrac{\hbar}{m\omega}}\xi$

の関係があります．）規格化条件，

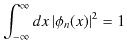
$\displaystyle \int_{-\infty}^{\infty}dx\,\vert\phi_{n}(x)\vert^{2}=1$

より，規格化定数 $A_{n}$ を次のように決定します．

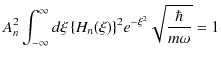	$\displaystyle A_{n}^{2}\int_{-\infty}^{\infty}d\xi\,\{H_{n}(\xi)\}^{2}e^{-\xi^{2}}\sqrt{\dfrac{\hbar}{m\omega}}=1$
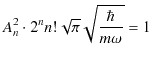$% latex2html id marker 2883 $\displaystyle \therefore$$	$\displaystyle A_{n}^{2}\cdot2^{n}n!\sqrt{\pi}\sqrt{\dfrac{\hbar}{m\omega}}=1$
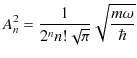$% latex2html id marker 2885 $\displaystyle \therefore$$	$\displaystyle A_{n}^{2}=\dfrac{1}{2^{n}n!\sqrt{\pi}}\sqrt{\dfrac{m\omega}{\hbar}}$
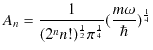$% latex2html id marker 2887 $\displaystyle \therefore$$	$\displaystyle A_{n}=\dfrac{1}{(2^{n}n!)^{\frac{1}{2}}\pi^{\frac{1}{4}}}(\dfrac{m\omega}{\hbar})^{\frac{1}{4}}$

したがって，固有関数 $\phi(x)$ は次式で表されます．（はとびとびの値をとりますので，離散固有関数であることがわかります．）

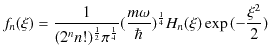	$\displaystyle f_{n}(\xi)=\dfrac{1}{(2^{n}n!)^{\frac{1}{2}}\pi^{\frac{1}{4}}}(\dfrac{m\omega}{\hbar})^{\frac{1}{4}}H_{n}(\xi)\exp⁡(-\dfrac{\xi^{2}}{2})$
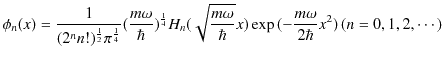$% latex2html id marker 2894 $\displaystyle \therefore$$	$\displaystyle \phi_{n}(x)=\dfrac{1}{(2^{n}n!)^{\frac{1}{2}}\pi^{\frac{1}{4}}}(\... ...frac{m\omega}{\hbar}}x)\exp⁡(-\dfrac{m\omega}{2\hbar}x^{2})\,(n=0,1,2,\cdots)$

この固有関数 $\phi(x)$ は規格直交系を形成します．

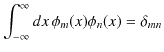
$\displaystyle \int_{-\infty}^{\infty}dx\,\phi_{m}(x)\phi_{n}(x)=\delta_{mn}$

12.3 演算子法による解法

このSectionでは，前Sectionのエルミート多項式の関係式をもとに，演算子法と呼ばれる方法で，1次元調和振動子の問題を取り扱ってみます．まず，

$\displaystyle \dfrac{d}{d\xi}\{H_{n}(\xi)\exp⁡(-\dfrac{\xi^{2}}{2})\}=H'_{n}(\xi)\exp⁡(-\dfrac{\xi^{2}}{2})-\xi H_{n}(\xi)\exp⁡(-\dfrac{\xi^{2}}{2})$

(12.12)

の恒等式より，

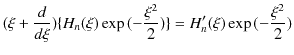
$\displaystyle (\xi+\dfrac{d}{d\xi})\{H_{n}(\xi)\exp⁡(-\dfrac{\xi^{2}}{2})\}=H'_{n}(\xi)\exp⁡(-\dfrac{\xi^{2}}{2})$

となります．ここで，(12.6)式，

$\displaystyle H'_{n}(\xi)=2nH_{n-1}(\xi)$

を右辺に代入すると，

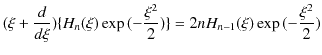
$\displaystyle (\xi+\dfrac{d}{d\xi})\{H_{n}(\xi)\exp⁡(-\dfrac{\xi^{2}}{2})\}=2nH_{n-1}(\xi)\exp⁡(-\dfrac{\xi^{2}}{2})$

となります．ここで，

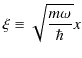
$\displaystyle \xi\equiv\sqrt{\dfrac{m\omega}{\hbar}}x$

と，

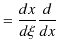$\displaystyle \dfrac{d}{d\xi}$	$\displaystyle =\dfrac{dx}{d\xi}\dfrac{d}{dx}$
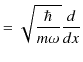	$\displaystyle =\sqrt{\dfrac{\hbar}{m\omega}}\dfrac{d}{dx}$

を代入して計算します．

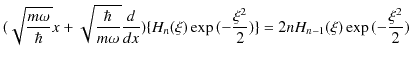	$\displaystyle (\sqrt{\dfrac{m\omega}{\hbar}}x+\sqrt{\dfrac{\hbar}{m\omega}}\dfr... ...}(\xi)\exp⁡(-\dfrac{\xi^{2}}{2})\}=2nH_{n-1}(\xi)\exp⁡(-\dfrac{\xi^{2}}{2})$
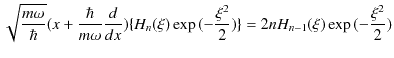$% latex2html id marker 2915 $\displaystyle \therefore$$	$\displaystyle \sqrt{\dfrac{m\omega}{\hbar}}(x+\dfrac{\hbar}{m\omega}\dfrac{d}{d... ...}(\xi)\exp⁡(-\dfrac{\xi^{2}}{2})\}=2nH_{n-1}(\xi)\exp⁡(-\dfrac{\xi^{2}}{2})$
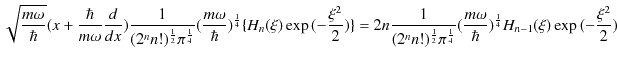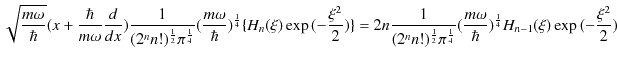$% latex2html id marker 2917 $\displaystyle \therefore$$	$\displaystyle \sqrt{\dfrac{m\omega}{\hbar}}(x+\dfrac{\hbar}{m\omega}\dfrac{d}{d... ...}(\dfrac{m\omega}{\hbar})^{\frac{1}{4}}H_{n-1}(\xi)\exp⁡(-\dfrac{\xi^{2}}{2})$
$% latex2html id marker 2919 $\displaystyle \therefore$$	$\displaystyle \sqrt{\dfrac{m\omega}{\hbar}}(x+\dfrac{\hbar}{m\omega}\dfrac{d}{d... ...}(\dfrac{m\omega}{\hbar})^{\frac{1}{4}}H_{n-1}(\xi)\exp⁡(-\dfrac{\xi^{2}}{2})$
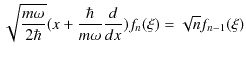$% latex2html id marker 2921 $\displaystyle \therefore$$	$\displaystyle \sqrt{\dfrac{m\omega}{2\hbar}}(x+\dfrac{\hbar}{m\omega}\dfrac{d}{dx})f_{n}(\xi)=\sqrt{n}f_{n-1}(\xi)$
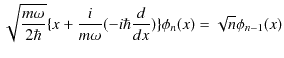$% latex2html id marker 2923 $\displaystyle \therefore$$	$\displaystyle \sqrt{\dfrac{m\omega}{2\hbar}}\{x+\dfrac{i}{m\omega}(-i\hbar\dfrac{d}{dx})\}\phi_{n}(x)=\sqrt{n}\phi_{n-1}(x)$
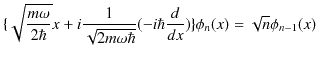$% latex2html id marker 2925 $\displaystyle \therefore$$	$\displaystyle \{\sqrt{\dfrac{m\omega}{2\hbar}}x+i\dfrac{1}{\sqrt{2m\omega\hbar}}(-i\hbar\dfrac{d}{dx})\}\phi_{n}(x)=\sqrt{n}\phi_{n-1}(x)$

ここで，左辺の中括弧の中の第2項の中にあるのは運動量演算子，

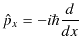
$\displaystyle \hat{p}_{x}=-i\hbar\dfrac{d}{dx}$

です．よって，新しく演算子，

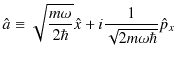
$\displaystyle \hat{a}\equiv\sqrt{\dfrac{m\omega}{2\hbar}}\hat{x}+i\dfrac{1}{\sqrt{2m\omega\hbar}}\hat{p}_{x}$

を導入すると，

$\displaystyle \hat{a}\phi_{n}(x)=\sqrt{n}\phi_{n-1}(x)$

が成立します．

　一方，(12.12)式，

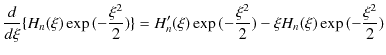
$\displaystyle \dfrac{d}{d\xi}\{H_{n}(\xi)\exp⁡(-\dfrac{\xi^{2}}{2})\}=H'_{n}(\xi)\exp⁡(-\dfrac{\xi^{2}}{2})-\xi H_{n}(\xi)\exp⁡(-\dfrac{\xi^{2}}{2})$

より，

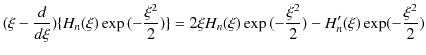	$\displaystyle (\xi-\dfrac{d}{d\xi})\{H_{n}(\xi)\exp⁡(-\dfrac{\xi^{2}}{2})\}=2\xi H_{n}(\xi)\exp⁡(-\dfrac{\xi^{2}}{2})-H'_{n}(\xi)\exp(-\dfrac{\xi^{2}}{2})$
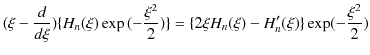$% latex2html id marker 2936 $\displaystyle \therefore$$	$\displaystyle (\xi-\dfrac{d}{d\xi})\{H_{n}(\xi)\exp⁡(-\dfrac{\xi^{2}}{2})\}=\{2\xi H_{n}(\xi)-H'_{n}(\xi)\}\exp(-\dfrac{\xi^{2}}{2})$

となります．ここで，エルミート多項式の関係式(12.7)式，

$\displaystyle H_{n+1}(\xi)=2\xi H_{n}(\xi)-2nH_{n-1}(\xi)$

の右辺第2項に，関係式(12.6)式，

$\displaystyle H'_{n}(\xi)=2nH_{n-1}(\xi)$

を代入します．

$\displaystyle H_{n+1}(\xi)=2\xi H_{n}(\xi)-H'_{n}(\xi)$

これを，先程の式に代入して，

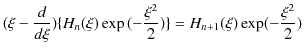
$\displaystyle (\xi-\dfrac{d}{d\xi})\{H_{n}(\xi)\exp⁡(-\dfrac{\xi^{2}}{2})\}=H_{n+1}(\xi)\exp(-\dfrac{\xi^{2}}{2})$

が成立します．ここで，

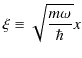
$\displaystyle \xi\equiv\sqrt{\dfrac{m\omega}{\hbar}}x$

と，

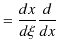$\displaystyle \dfrac{d}{d\xi}$	$\displaystyle =\dfrac{dx}{d\xi}\dfrac{d}{dx}$
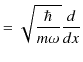	$\displaystyle =\sqrt{\dfrac{\hbar}{m\omega}}\dfrac{d}{dx}$

を代入して計算します．

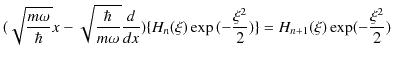	$\displaystyle (\sqrt{\dfrac{m\omega}{\hbar}}x-\sqrt{\dfrac{\hbar}{m\omega}}\dfr... ...{H_{n}(\xi)\exp⁡(-\dfrac{\xi^{2}}{2})\}=H_{n+1}(\xi)\exp(-\dfrac{\xi^{2}}{2})$
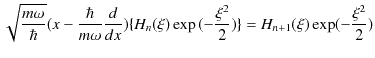$% latex2html id marker 2952 $\displaystyle \therefore$$	$\displaystyle \sqrt{\dfrac{m\omega}{\hbar}}(x-\dfrac{\hbar}{m\omega}\dfrac{d}{d... ...{H_{n}(\xi)\exp⁡(-\dfrac{\xi^{2}}{2})\}=H_{n+1}(\xi)\exp(-\dfrac{\xi^{2}}{2})$
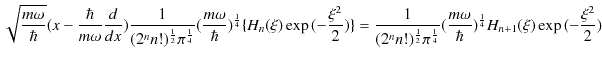$% latex2html id marker 2954 $\displaystyle \therefore$$	$\displaystyle \sqrt{\dfrac{m\omega}{\hbar}}(x-\dfrac{\hbar}{m\omega}\dfrac{d}{d... ...}(\dfrac{m\omega}{\hbar})^{\frac{1}{4}}H_{n+1}(\xi)\exp⁡(-\dfrac{\xi^{2}}{2})$
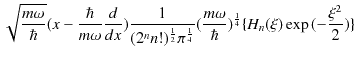$% latex2html id marker 2956 $\displaystyle \therefore$$	$\displaystyle \sqrt{\dfrac{m\omega}{\hbar}}(x-\dfrac{\hbar}{m\omega}\dfrac{d}{d... ...\dfrac{m\omega}{\hbar})^{\frac{1}{4}}\{H_{n}(\xi)\exp⁡(-\dfrac{\xi^{2}}{2})\}$
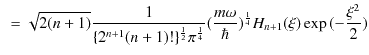	$\displaystyle \,\,\,=\sqrt{2(n+1)}\dfrac{1}{\{2^{n+1}(n+1)!\}^{\frac{1}{2}}\pi^... ...}(\dfrac{m\omega}{\hbar})^{\frac{1}{4}}H_{n+1}(\xi)\exp⁡(-\dfrac{\xi^{2}}{2})$
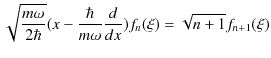$% latex2html id marker 2959 $\displaystyle \therefore$$	$\displaystyle \sqrt{\dfrac{m\omega}{2\hbar}}(x-\dfrac{\hbar}{m\omega}\dfrac{d}{dx})f_{n}(\xi)=\sqrt{n+1}f_{n+1}(\xi)$
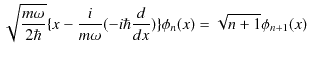$% latex2html id marker 2961 $\displaystyle \therefore$$	$\displaystyle \sqrt{\dfrac{m\omega}{2\hbar}}\{x-\dfrac{i}{m\omega}(-i\hbar\dfrac{d}{dx})\}\phi_{n}(x)=\sqrt{n+1}\phi_{n+1}(x)$
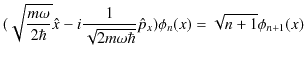$% latex2html id marker 2963 $\displaystyle \therefore$$	$\displaystyle (\sqrt{\dfrac{m\omega}{2\hbar}}\hat{x}-i\dfrac{1}{\sqrt{2m\omega\hbar}}\hat{p}_{x})\phi_{n}(x)=\sqrt{n+1}\phi_{n+1}(x)$

新しく演算子，

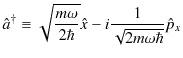
$\displaystyle \hat{a}^{\dagger}\equiv\sqrt{\dfrac{m\omega}{2\hbar}}\hat{x}-i\dfrac{1}{\sqrt{2m\omega\hbar}}\hat{p}_{x}$

を導入すると，

$\displaystyle \hat{a}^{\dagger}\phi_{n}(x)=\sqrt{n+1}\phi_{n+1}(x)$

が成立します．

　新しい演算子の性質を調べていきましょう．演算子は，

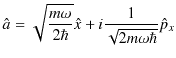	$\displaystyle \hat{a}=\sqrt{\dfrac{m\omega}{2\hbar}}\hat{x}+i\dfrac{1}{\sqrt{2m\omega\hbar}}\hat{p}_{x}$
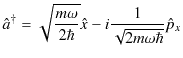	$\displaystyle \hat{a}^{\dagger}=\sqrt{\dfrac{m\omega}{2\hbar}}\hat{x}-i\dfrac{1}{\sqrt{2m\omega\hbar}}\hat{p}_{x}$

です．これらを辺々加えて，

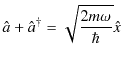	$\displaystyle \hat{a}+\hat{a}^{\dagger}=\sqrt{\dfrac{2m\omega}{\hbar}}\hat{x}$
$% latex2html id marker 2972 $\displaystyle \therefore$$	$\displaystyle \hat{x}=\sqrt{\dfrac{\hbar}{2m\omega}}(\hat{a}+\hat{a}^{\dagger})$

と表せます．辺々引くと，

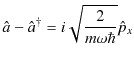	$\displaystyle \hat{a}-\hat{a}^{\dagger}=i\sqrt{\dfrac{2}{m\omega\hbar}}\hat{p}_{x}$
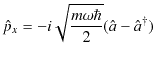$% latex2html id marker 2975 $\displaystyle \therefore$$	$\displaystyle \hat{p}_{x}=-i\sqrt{\dfrac{m\omega\hbar}{2}}(\hat{a}-\hat{a}^{\dagger})$

と表せます．また，

	$\displaystyle \hat{a}\phi_{n}(x)=\sqrt{n}\phi_{n-1}(x)$
	$\displaystyle \hat{a}^{\dagger}\phi_{n}(x)=\sqrt{n+1}\phi_{n+1}(x)$

の関係式が成立しました．よって，

$\displaystyle \hat{a}^{\dagger}\hat{a}\phi_{n}(x)$	$\displaystyle =\hat{a}^{\dagger}\sqrt{n}\phi_{n-1}(x)$
	$\displaystyle =\sqrt{n}(\sqrt{n}\phi_{n}(x))$

すなわち，

$\displaystyle \hat{a}^{\dagger}\hat{a}\phi_{n}(x)=n\phi_{n}(x)$

と，

$\displaystyle \hat{a}\hat{a}^{\dagger}\phi_{n}(x)$	$\displaystyle =\hat{a}\sqrt{n+1}\phi_{n+1}(x)$
	$\displaystyle =\sqrt{n+1}(\sqrt{n+1}\phi_{n}(x))$

すなわち，

$\displaystyle \hat{a}\hat{a}^{\dagger}\phi_{n}(x)=(n+1)\phi_{n}(x)$

が成立します．したがって，

	$\displaystyle (\hat{a}\hat{a}^{\dagger}-\hat{a}^{\dagger}\hat{a})\phi_{n}(x)=\phi_{n}(x)$
$% latex2html id marker 2990 $\displaystyle \therefore$$	$\displaystyle [\hat{a},\hat{a}^{\dagger}]=1$

の交換関係が成り立ちます．ここで，個数演算子，

$\displaystyle \hat{N}\equiv\hat{a}^{\dagger}\hat{a}$

を定義すると，先程の式より，

$\displaystyle \hat{N}\phi_{n}(x)=n\phi_{n}(x)$

の固有値方程式が成立します．つまり，個数演算子の固有値は量子数になります．また，

$\displaystyle \hat{N}\hat{a}\phi_{n}(x)$	$\displaystyle =\hat{a}^{\dagger}\hat{a}\hat{a}\phi_{n}(x)$
	$\displaystyle =(\hat{a}\hat{a}^{\dagger}-1)\hat{a}\phi_{n}(x)$
	$\displaystyle =(\hat{a}\hat{a}^{\dagger}\hat{a}-\hat{a})\phi_{n}(x)$
	$\displaystyle =(n\hat{a}-\hat{a})\phi_{n}(x)$
	$\displaystyle =(n-1)\hat{a}\phi_{n}(x)$

が成立するので， $\hat{a}\phi_{n}(x)$ は固有値をもつ， $\hat{N}$ の固有関数になっています．このように， $\hat{a}$ はの値を1つ下げる演算子なので消滅演算子といいます．同様に，

$\displaystyle \hat{N}\hat{a}^{\dagger}\phi_{n}(x)$	$\displaystyle =\hat{a}^{\dagger}\hat{a}\hat{a}^{\dagger}\phi_{n}(x)$
	$\displaystyle =\hat{a}^{\dagger}(\hat{a}^{\dagger}\hat{a}+1)\phi_{n}(x)$
	$\displaystyle =(n+1)\hat{a}^{\dagger}\phi_{n}(x)$

が成立するので， $\hat{a}^{\dagger}\phi_{n}(x)$ は固有値をもつ， $\hat{N}$ の固有関数になっています．このように， $\hat{a}^{\dagger}$ はの値を1つ上げる演算子なので生成演算子といいます．

　生成消滅演算子を使ってエネルギー固有値を求めましょう．ハミルトニアンは次のようになります．

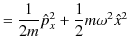$\displaystyle \hat{H}(\hat{x},\hat{p}_{x})$	$\displaystyle =\dfrac{1}{2m}\hat{p}_{x}^{2}+\dfrac{1}{2}m\omega^{2}\hat{x}^{2}$
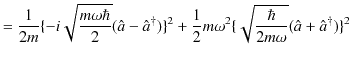	$\displaystyle =\dfrac{1}{2m}\{-i\sqrt{\dfrac{m\omega\hbar}{2}}(\hat{a}-\hat{a}^... ...{2}m\omega^{2}\{\sqrt{\dfrac{\hbar}{2m\omega}}(\hat{a}+\hat{a}^{\dagger})\}^{2}$
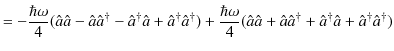	$\displaystyle =-\dfrac{\hbar\omega}{4}(\hat{a}\hat{a}-\hat{a}\hat{a}^{\dagger}-... ...}\hat{a}^{\dagger}+\hat{a}^{\dagger}\hat{a}+\hat{a}^{\dagger}\hat{a}^{\dagger})$
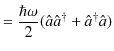	$\displaystyle =\dfrac{\hbar\omega}{2}(\hat{a}\hat{a}^{\dagger}+\hat{a}^{\dagger}\hat{a})$
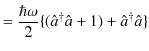	$\displaystyle =\dfrac{\hbar\omega}{2}\{(\hat{a}^{\dagger}\hat{a}+1)+\hat{a}^{\dagger}\hat{a}\}$
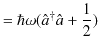	$\displaystyle =\hbar\omega(\hat{a}^{\dagger}\hat{a}+\dfrac{1}{2})$
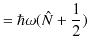	$\displaystyle =\hbar\omega(\hat{N}+\dfrac{1}{2})$

このハミルトニアンを固有関数 $\phi_{n}(x)$ に作用させます．

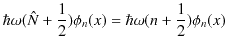
$\displaystyle \hbar\omega(\hat{N}+\dfrac{1}{2})\phi_{n}(x)=\hbar\omega(n+\dfrac{1}{2})\phi_{n}(x)$

故に，エネルギー固有値は，

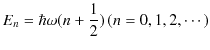
$\displaystyle E_{n}=\hbar\omega(n+\dfrac{1}{2})\,(n=0,1,2,\cdots)$

となります．この結果は前のSectionと同じになっています．