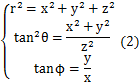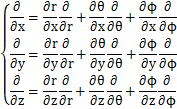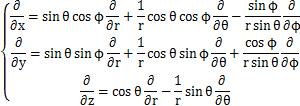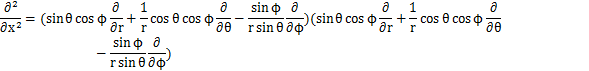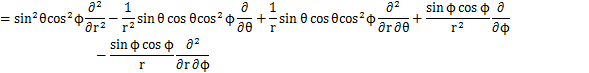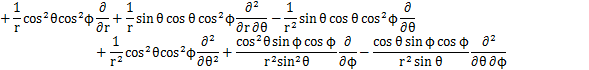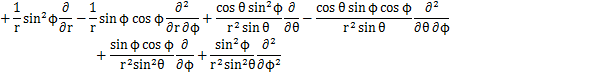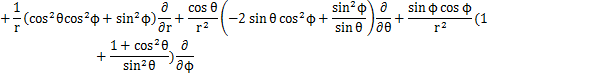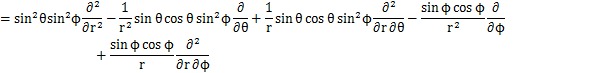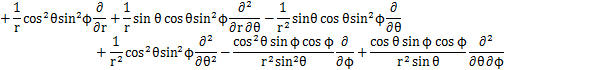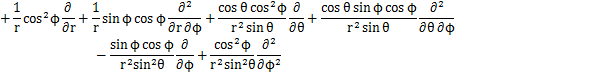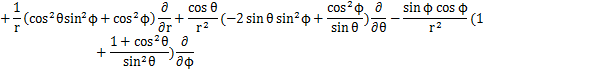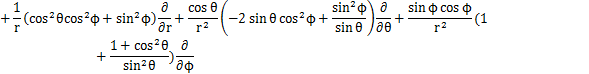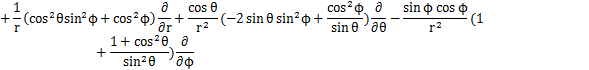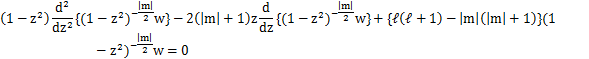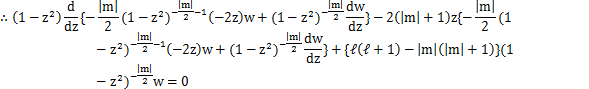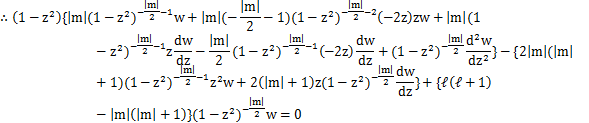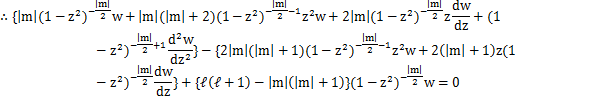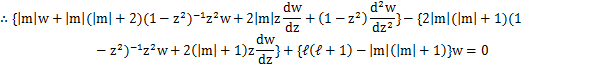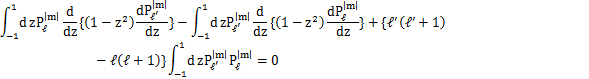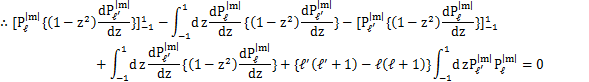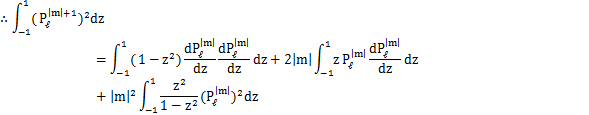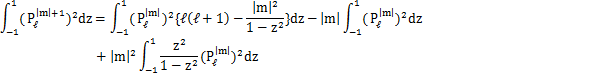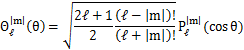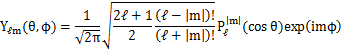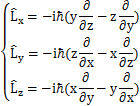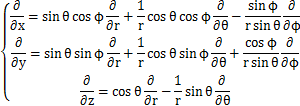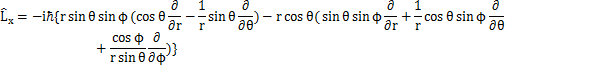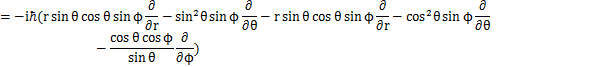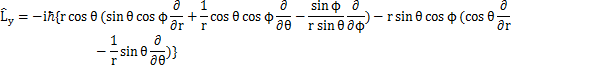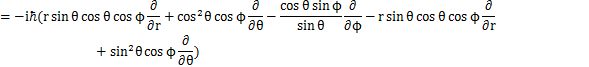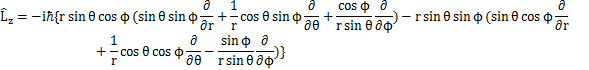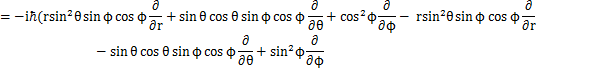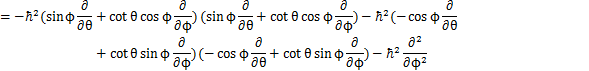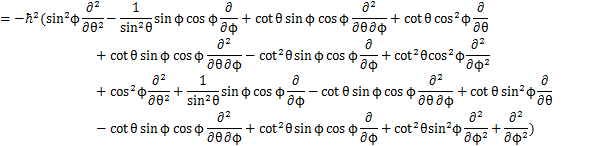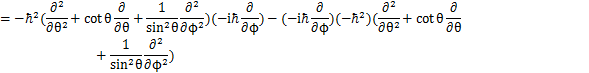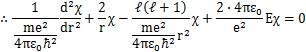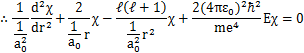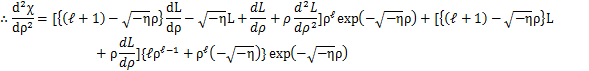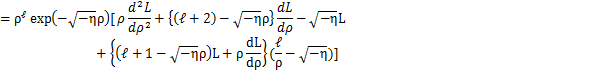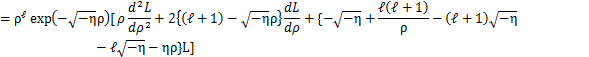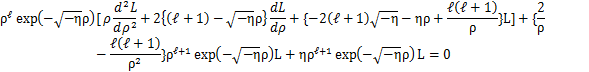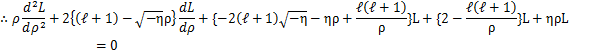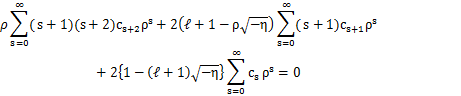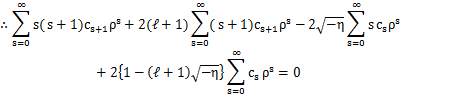Chapter13 束縛状態3:例4(中心力場内の粒子)
13.1 中心力場内の粒子のシュレディンガー方程式
原点からの距離rにのみ依存する力を中心力といいます.その中心力の場の中で1個だけの粒子が運動している系を取り扱ってみましょう.このような系の具体例としては,水素原子が挙げられます.原子の構造のChapterでボーアの前期量子論を議論し,水素原子を取り扱いましたが,それは不完全なものでした.本Chapterでは完成した波動力学を使い,完全に説明します.
中心力場が生じている場合,そのポテンシャルは原点からの距離rだけの関数V(r)と表すことができます.定常状態を考えると,時間に依存しないシュレディンガー方程式は次式のようになります.
この方程式を解くために,直交座標の代わりに球面座標を用います.
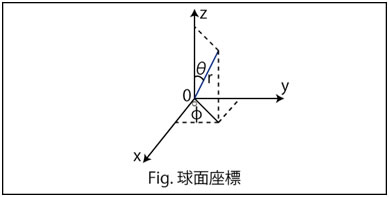
このとき,
が成立します.合成関数の偏微分の公式は,
です.ここで,(2)式の第1式をx,y,zで偏微分して計算します.
(2)式の第2式をx,y,zで偏微分して計算します.
(2)式の第3式をx,y,zで偏微分して計算します.
故に,
となります.これらの式からラプラシアンを計算します.
ここで,
とおくと,
となります.この式が球面座標で表されたラプラシアンです.したがって,時間に依存しないシュレディンガー方程式は次式のようになります.
この微分法方程式を解くために,変数分離の方法にしたがって,
と,おきます.このとき,方程式は次のように変形されます.
最後の式は,左辺がrだけの関数で,右辺はθとφだけの関数になっています.これらが等式で結ばれるためには,ある定数に等しくならなければなりません.そこで,この定数をλとおきます.このとき,
という動径部分の方程式と,
という角度部分の方程式が成立します.
最後の式をさらに変形していきます.Λに式を代入すると,
となります.ここで,さらに変数分離して,
と,おきます.このとき,方程式は次のように変形されます.
最後の式で,左辺はθだけの関数で,右辺はφだけの関数になっています.これらが等号で結ばれるためには,定数に等しくならなければなりません.そこで,その定数をνとおきます.このとき,
というθ部分の方程式と,
というφ部分の方程式が成立します.
13.2 φ部分の微分方程式の解
φ部分の方程式の一般解を求めましょう.ν=0の場合は,
となります.ただし,AとBは定数です.Φはφについて2πの周期をもっていなければなりません.そのためには,
が解になります.しかし,この解は物理的に意味をなしません.次に,ν<0の場合,微分方程式は,
という解をもちます(AとBは定数です.)が,Φはφについて2πの周期をもっていなければならないので,不適になります.ν>0の場合,微分方程式は,
という解をもちます.(AとBは定数です.)また,![]() が整数でないと,φについての2π毎の周期性が成り立たないので,
が整数でないと,φについての2π毎の周期性が成り立たないので,
とおくことにします.このとき,
となります.Φについてだけでも規格化条件を課しておきましょう.
規格化条件より,最後の式が1に等しくなります.
符号は正の方をとると,
となります.また,この関数は直交していることも確かめられます.m≠nのとき,
となります.
13.3 θ部分の微分方程式
次に,θ部分の方程式を変形していきましょう.![]() より,θ部分の方程式は次のようになります.
より,θ部分の方程式は次のようになります.
ここで,
と変数変換します.このとき,
になります.また,
と,おきます.方程式は次のように変形されます.
ここで,θは0からπまで変化するので,zは1から-1まで変わります.この方程式でm=0とおいた式は,
となります.(4)式を解くために,Pはzのべき級数で展開できると仮定します.すなわち,
と,おきます.Pをzで微分していくと次式を得ます.
これらの式を(4)式に代入します.
最後の式において,![]() の係数を0とおくと,
の係数を0とおくと,
となります.べき級数が有限項で終わるためには,
でなければなりません.この式を(3)式に代入すると,
となります.ここで,mに絶対値を付けたのは,正負にかかわらず,同じ方程式になるからです.(5)式をルジャンドル陪微分方程式といいます.(![]() のことをルジャンドル陪関数といいます.)ここで,m=0とおいたものをルジャンドル微分方程式といいます.すなわち,
のことをルジャンドル陪関数といいます.)ここで,m=0とおいたものをルジャンドル微分方程式といいます.すなわち,
となります.ルジャンドル微分方程式(6)式を満たす多項式![]() をルジャンドル多項式といいます.
をルジャンドル多項式といいます.
13.4 ルジャンドル多項式
ルジャンドル多項式は母関数,
を用いて定義することができます.この式を![]() で展開すると,
で展開すると,
となります.ここで,
によってルジャンドル多項式![]() を定義することにします.具体的に次数の小さな例を挙げると,
を定義することにします.具体的に次数の小さな例を挙げると,
のようになります.次に,この母関数による定義の![]() が,確かにルジャンドル微分方程式(6)式の解になっていることを示しておきます.この式をzで偏微分して変形していくと,
が,確かにルジャンドル微分方程式(6)式の解になっていることを示しておきます.この式をzで偏微分して変形していくと,
となります.故に,![]() の係数を比較して,
の係数を比較して,
の関係式を得ます.また,![]() の母関数による定義式を,同様にtで偏微分して変形していくと,
の母関数による定義式を,同様にtで偏微分して変形していくと,
となります.故に,![]() の係数を比較して,
の係数を比較して,
を得ます.この式をzで微分すると,
となります.2×(8)+(2ℓ+1)×(7)より,
となります.![]() より,
より,
となります.![]() より,
より,
となります.(10)+z×(11)より,
となります.この式をzで微分して計算します.
(12)+ℓ×(11)より,
となります.最後の式はルジャンドル微分方程式(6)です.したがって,母関数によって定義された![]() が微分方程式を満たすことが確認されました.
が微分方程式を満たすことが確認されました.
ℓの違う2つのルジャンドル多項式は直交します.すなわち,
が成立します.この式を証明しましょう.ルジャンドル微分方程式(6)式,
において,![]() を掛けて,-1から1まで積分します.
を掛けて,-1から1まで積分します.
この式の第1項は,
となります.故に,
となります.ここで,ℓとmの役割を交換して差をとり計算します.
(証明終)次に,ℓ=mの場合を考えましょう.ルジャンドル多項式の母関数についての式,
の両辺を2乗します.
-1から1まで積分すると,
となります.このとき,
とおくと,
となり,上の積分の式の左辺は,
となります.ここで,
なので,
となり,
が成立します.ℓ≠mの場合も含めてまとめると,
となります.
13.5 θ部分の微分方程式の解(ルジャンドル陪関数)
θ部分の微分方程式である,ルジャンドル陪微分方程式(5)式,
を解き,θ部分の解を求めましょう.(![]() はルジャンドル陪関数といいましたね.)
はルジャンドル陪関数といいましたね.)
ルジャンドル微分方程式(6)式,
を,
としておきます.この式をzで微分して整理します.(1回目)
この式をzで微分して整理します.(2回目)
この式をzで微分して整理します.(3回目)
この式をzで微分して整理します.(|m|回目)
ここで,
とおくと,
となります.さらに,
とおいて計算します.
最後の式は,ルジャンドル陪関数![]() についての微分方程式と一致しています.つまり,解
についての微分方程式と一致しています.つまり,解![]() はwです.
はwです.
![]() はℓ次の多項式なので,
はℓ次の多項式なので,
の条件が成り立たなければなりません.
さて,ルジャンドル陪関数について,
が成立します.以下,この式を証明します.まず,ℓ≠ℓ´の場合を取り扱います.
において,両辺に![]() をかけます.
をかけます.
ここで,ℓとℓ´を入れ替えて,
となります.辺々引いて,
となります.-1から1までzで積分すると,
となります.次にℓ=ℓ´の場合を考えます.ルジャンドル陪関数,
をzで微分します.
両辺に![]() をかけて変形します.
をかけて変形します.
ここで,右辺第1項と第2項は部分積分法により,次のようになります.
したがって,
となります.|m|を1ずつ減らしていくと,
となります.故に,
となります.ここで,
の関係式が成立したので,
となります.よって,
の関係式が証明されました.
規格直交系の形でΘ(θ)を与えると,
となります.このとき,規格直交条件は次式で表されます.(![]() )
)
13.6 角度部分の微分方程式の解(球面調和関数)
θ部分の解は前Sectionの最後に与えられました.一方,φ部分の解は,
でした.角度部分の解は,
の形で与えられます.結論として,解は,
となります.![]() を球面調和関数といいます.球面調和関数は条件,
を球面調和関数といいます.球面調和関数は条件,
を満たし,規格直交系を形成します.
13.7 軌道角運動量
中心力場における量子の回転を,軌道角運動量を用いて取り扱ってみましょう.オブザーバブルのChapterで前出したように,角運動量演算子は,
と表されました.ここで,球面座標を用いることにします.このとき,最初のSectionで出てきたように,
の関係がありました.したがって,
となります.故に,
となります.![]() に対する固有方程式は,固有関数をY,固有値を
に対する固有方程式は,固有関数をY,固有値を![]() とおくと,
とおくと,
となりますが,これは前のSectionの角度部分の微分方程式,
と同じ形をしています.したがって,![]() であり,固有方程式の固有関数は球面調和関数になります.つまり,
であり,固有方程式の固有関数は球面調和関数になります.つまり,
の関係が成立します.故に,![]() の固有値は
の固有値は![]() となります.(正確な表現ではありませんが,軌道角運動量
となります.(正確な表現ではありませんが,軌道角運動量![]() の大きさは
の大きさは![]() である,ということがよくあります.)
である,ということがよくあります.)
次に,![]() ,
,![]() ,
,![]() のうち,最も簡単な形をしている
のうち,最も簡単な形をしている![]() について固有方程式を考えましょう.固有関数をΦ,固有値を
について固有方程式を考えましょう.固有関数をΦ,固有値を![]() とおくと,
とおくと,
となります.この微分方程式の一般解は,
になります.ただし,Aは積分定数です.ここで,φが2π増減しても,Φは等しい値に戻れなければなりません.よって,mは整数です.
ここで,Φについて,規格化条件を課しておきます.
符号は正の方をとると,
となります.これはシュレディンガー方程式のφ部分の解Φと一致します.ここで,固有方程式,
の両辺に関数Θ(θ)を掛けてみると,
となります.すなわち,![]() の固有関数も球面調和関数になります.
の固有関数も球面調和関数になります.![]() と
と![]() の固有関数がともに球面調和関数であることが判明しました.
の固有関数がともに球面調和関数であることが判明しました.![]() と
と![]() の固有関数が同時固有関数になっていることを確かなものにするためには,一般論に従って交換可能である条件,
の固有関数が同時固有関数になっていることを確かなものにするためには,一般論に従って交換可能である条件,
が成立することが必要十分条件になります.実際に計算してみます.
まとめると,![]() と
と![]() の固有関数は同時固有関数である球面調和関数であり,固有値はそれぞれ
の固有関数は同時固有関数である球面調和関数であり,固有値はそれぞれ![]() と
と![]() になります.
になります.
ℓは軌道角運動量の大きさのようなものを表す量で,方位量子数といいます.mは軌道角運動量のz成分を示す量で,磁気量子数といいます.そして,次のような跳び跳びの値をとりました.
このとき,ひとつのℓに対して,mのとりうる値は(2ℓ+1)個あります.すなわち,![]() の固有値
の固有値![]() は(2ℓ+1)重に縮退しています.
は(2ℓ+1)重に縮退しています.
ℓとmの関係を直観的に把握するため,具体的にm=2の場合について考えておきましょう.(ただし,以下の議論は理解を助けるため,古典的な考え方も利用していることを了承して下さい.)この場合,![]() の固有値は,
の固有値は,
になります.よって,
になります.m=-2,-1,0,1,2の値をとるので,軌道角運動量のz成分は,![]() になります.以上の関係を古典的に図示すると,次のようになります.
になります.以上の関係を古典的に図示すると,次のようになります.
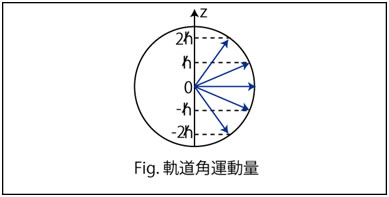
ℓ=2のとき,軌道角運動量として許されるのは,上図の5本のベクトルだけになります.(5重に縮退しています.)
13.8 水素原子の動径部分の微分方程式
動径部分の方程式,
において,
を代入すると,
が得られます.ここで,
と,おきます.この式をrで微分していきます.
微分方程式に代入して計算します.
この方程式は1次元シュレディンガー方程式とよく似ていますが,{ }内の第2項の部分が異なります.これは遠心力に相当するポテンシャルです.
水素原子では中心に+eの電荷をもつ陽子があり,その周りを-eの電荷をもつ電子が円運動しています.その間に働く力はクーロン力であり,そのポテンシャルは,
で与えられます.このとき,微分方程式は次のように変形されていきます.
ここで,
とおくと,
となります.さらに,
とおくと,(E<0より,η<0となります.)
となります.ρが大きいとき,第2項と第3項を落として,この微分方程式は,
となります.その解は,
です.r→∞,(ρ→∞)でχ→0の境界条件を満たすためには指数関数のべきは負でなければなりません.すなわち,
となります.任意のρでのχを解くために,
と,おきます.χをρで微分していくと,
となります.これらをもとの微分方程式に代入して計算します.
13.9 水素原子のエネルギー固有値(ボーア前期量子論との一致)
(13)式において,L(ρ)がρのべき級数に展開できると仮定してみます.
Lをρで微分していくと,次式を得ます.
これらを微分方程式(13)式に代入して計算します.
両辺の![]() の係数を比較して,
の係数を比較して,
を得ます.級数が有限項で終わるためには,あるsの値n´で,
とならなければなりません.ここで,
と,おき,nを主量子数と名付けます.このとき,
という水素原子のエネルギー準位の式が導出されます.この式は原子の構造のChapterのボーアの前期量子論での式と完全に一致します.ボーアの理論での天下り的な仮定をせずに,シュレディンガー方程式を用いた完成された量子力学によって,一段と高いレベルから同じ結果を再現することができたのです.