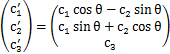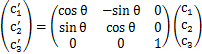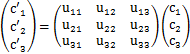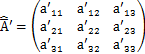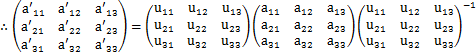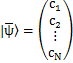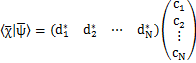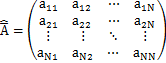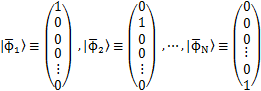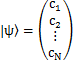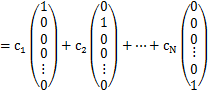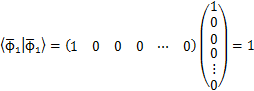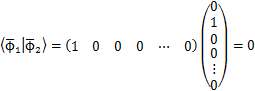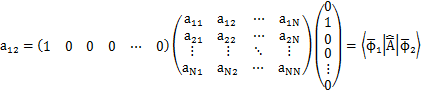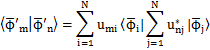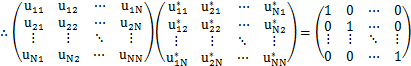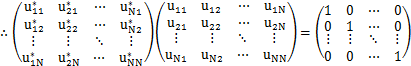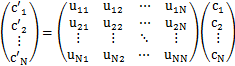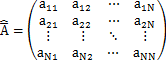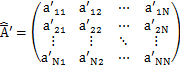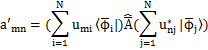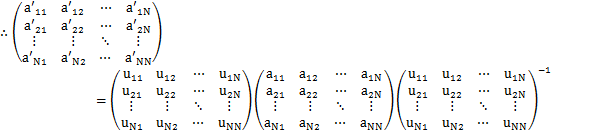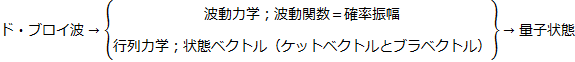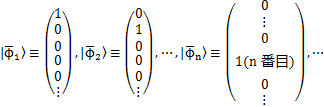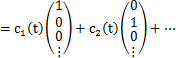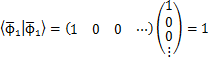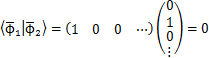J Simplicity 行列力学

Part3 量子力学の展開

Chapter14 行列力学

14.1 数学的準備１:３次元実ベクトル空間の線形代数

このChapterでの議論の準備として，このSectionと次のSectionで線形代数の知識を整理しておきます．直交座標で表される３次元空間の実ベクトル，

を考えましょう．（各成分はそれぞれ実数で，順番にx成分，y成分，z成分を表します．）この現実の空間についてのベクトルで張られる空間を３次元実ベクトル空間といいます．ベクトルを縦に表記して，列ベクトルとして表すこともできます．

左辺の記号をケットといい，列ベクトルのことをケットベクトルといいます．ψの上に示したバーは行列であることを表す記号です．このケットベクトルと対をなす行ベクトルを約束しましょう．

左辺の記号をブラといい，この行ベクトルのことをブラベクトルといいます．ブラベクトルはケットベクトルの転置行列になります．（行と列を入れ換えた行列を転置行列といいます．）ブラとケットはbracket（括弧）という言葉からの造語であり，ディラックの発案によります．次に，ブラベクトルとケットベクトルを使い，内積と呼ばれる量を定義します．すなわち，

のブラベクトルとケットベクトルに対して，

の量が内積です．特に，内積の値が0のとき，直交しているといいます．また，ベクトルの大きさをノルムといいますが，自分自身との内積はノルムの２乗になります．自分自身との内積が1のとき，規格化されているといいます．つまり，規格化条件は，

と表せます．
　３次元空間のベクトルに対して，何らかの操作をして，他のベクトルをつくる演算を考えましょう．例えば，あるベクトルを軸回りに角度θだけ回転させて新たにベクトルをつくった場合，

と変換されます．これを，ケットベクトルを使って表すと，

となります．さらに３×３行列を使い変形すると，

となります．あるベクトルから何らかの操作をして，他のベクトルをつくる場合，上の式のような形式で表されることになります．これを，一般に，

と表します．ただし，はケットベクトルに作用する行列であり，作用素行列と名付けることにします．ハットは作用素であることを示し，バーは行列であることを表しています．記号が二重になっていますが，意味を考えてこのようにしました．一般に，作用素行列は，

のように，行列要素をもちます．ここで，例における作用素行列に対して，

という関係が確かめられます．（αとβは実数の定数です．）一般に，

という関係を満たす作用素行列を線形作用素行列といいます．
　ここで，標準基底ベクトルといわれるベクトルを導入します．具体的に示すと，ケットベクトルの標準基底ベクトルは，

で定義されます．つまり，それぞれの座標軸の向きの単位ベクトルが標準基底ベクトルです．標準基底ベクトルにより，任意のケットベクトルは次のように表すことができます．

　

　

　

ブラベクトルに対しても，同様に標準基底ベクトルを定義することができます．

これらの標準基底ベクトルにより，任意のブラベクトルが表されることはケットベクトルの場合と同様です．

標準基底ベクトルの間には，次の規格直交条件が成立します．

ただし，右辺はクロネッカーのデルタといい，次のように定義されます．

この規格直交条件は，具体的に，

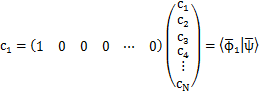
のように，計算して確かめられます．規格直交条件を満たしている標準基底ベクトルは規格直交系を成しているといいます．標準基底ベクトルを使うと，ケットベクトルの行列要素は，例えば，

のように，表されます．したがって，

です．また，作用素行列の行列要素は，例えば，

のように，表されます．したがって，

です．
　標準基底ベクトルは直交座標の座標軸の向きの単位ベクトルですが，例えば，座標軸を回転させるような操作を考えてみましょう．そのときには，新しい基底ベクトルがつくられることになります．座標軸の回転に限らず，ある直交座標の基底ベクトルから何らかの操作をして，他の直交座標の基底ベクトルをつくることを基底の変換と言います．基底の変換を式で書くと，

となります．まとめて書くと，

と表されます．左辺のダッシュがついたケットベクトルが変換後の基底ベクトルであり，右辺のダッシュの付いていないケットベクトルが変換前の基底ベクトルです．また，右辺のuの実数の行列要素の行列が変換の関係を表します．（この行列をで表すことにします．）この式のケットベクトルの転置をとり，ブラベクトルをつくると，

です．変換後の基底ベクトルは新しい直交座標の座標軸の向きの単位ベクトルなので，規格直交系をなしていなければなりません．すなわち，

が成立します．ここで，左辺を計算すると，

です．よって，

となります．前述したように，行と列を入れ換えた行列を転置行列といいますが，の転置行列をで表します．このとき，上の式は，

となります．ただし，は単位行列です．したがって，の転置行列はの逆行列になります．

この関係を満たす行列を直交行列と言います．すなわち，

“直交座標系の基底ベクトルの変換を表す行列は直交行列です．”

という結論が得られました．（直交行列による変換を直交変換と言います．）ここで，の両辺に左から，を作用させると，

という関係が成立することも確かめられます．また，基底ベクトルの逆変換も求めておきましょう．変換式は，

でしたが，両辺にをかけてmについて和をとり，計算します．

添え字のiをnに書き直すと，

という変換後の基底ベクトルを変換前の基底ベクトルに逆変換する式が導かれました．
　直交行列による基底ベクトルの変換に伴い，任意のベクトルと作用素行列はどのように変換するのでしょうか？まず，ケットベクトルですが，変換前の基底ベクトルで表しておき，変換前の基底ベクトルを変換後の基底ベクトルで表した逆変換の式を代入して計算すると，

　

　

となります．この式と，を変換後の基底ベクトルで表した式，

を比較して，

となります．故に，

を得ます．この式の両辺の転置行列をとると，

というブラベクトルの変換式も求められます．内積の変換式も見ておきましょう．

となるので，内積は直交変換に対して不変です．次に，作用素行列の変換式も求めておきましょう．もとの作用素行列，

に対して，基底を変換した場合の新しい作用素行列を，

とします．行列要素は，

から，

へ変換されます．最後の式は次のように計算されます．

故に，作用素行列の変換式が求められました．また，変換式の両辺に左から，右からを作用させて計算すると，

となります．

14.2 数学的準備２:N次元複素ベクトル空間の線形代数

前のSectionのベクトル空間の次元をN次元に（Nは自然数とします．），行列要素を複素数に拡張しましょう．この抽象化されたベクトル空間をN次元複素ベクトル空間と言います．
　ケットベクトルは，

と表されます．このケットベクトルに対するブラベクトルは，

で定義されます．ブラベクトルはケットベクトルの転置共役行列です．また，内積は，

です．作用素行列は，

の式のであることには変わりはありませんが，

のように，行列要素をもちます．一般に，

という関係を満たす作用素行列のことを線形作用素行列といいます．（αとβは複素数の定数．）
　標準基底ベクトルは，

で定義されます．この標準基底ベクトルにより，任意のケットベクトルは次のように表すことができます．

ブラベクトルに対しても，同様に標準基底ベクトルを定義することができます．

これらの標準基底ベクトルにより，任意のブラベクトルが表されることはケットベクトルの場合と同様です．

標準基底ベクトルの間には，次の規格直交条件が成立します．

この式は，具体的に，

のように，計算して確かめられます．規格直交条件を満たしている標準基底ベクトルは規格直交系を成しているといいます．また，標準基底ベクトルを使うと，ケットベクトルの行列要素は，例えば，

のように，表されます．従って，

です．また，作用素行列の行列要素は，例えば，

のように，表されます．したがって，

となります．標準基底ベクトルに限らず，ある規格直交系を成す基底ベクトルから何らかの操作をして，他の規格直交系を成す基底ベクトルをつくることを基底の変換と言います．基底の変換を式で書くと，

と表されます．（行列の複素共役を使って定義しましたが，このようにすれば，後の共役の関係がすっきりとしたものになります．）この式の両辺の複素共役をとり，さらにケットベクトルを転置して，

となります．新しい基底ベクトルも規格直交系を成していますので，

が成立します．ここで，左辺を計算すると，

　

　

となります．よって，

となります．の転置をとり行列要素を複素共役にした行列を転置共役行列と言いますが，これをで表します．このとき，上の式は，

となります．従って，の転置共役行列はの逆行列になります．

この関係式を満たす行列をユニタリー行列と言います．すなわち，

“規格直交系の基底ベクトルの変換を表す行列はユニタリー行列です．”

という結論が得られました．（ユニタリー行列による変換をユニタリー変換と言います．）ここで，の両辺に左からを作用させると，

という関係式も成立します．また，基底ベクトルの逆変換も求めておきましょう．変換式は，

でしたが，両辺にをかけてmについて和をとり，計算します．

添え字のiをnに置き直すと，

という新しい基底ベクトルを古い基底ベクトルに逆変換する式が導かれました．
　ユニタリー行列による基底ベクトルの変換に伴い，任意のベクトルと作用素行列はどのように変換するでしょうか？まず，ケットベクトルですが，変換前の基底ベクトルで表し，それを変換後の基底ベクトルに逆変換した式を代入すると，

　

　

となります．この式と，変換後の基底ベクトルで表した式，

を比較して，

となります．故に，

を得ます．最後の式の両辺の転置共役をとると，

というブラベクトルの変換式も求められます．内積の変換式も求めておきましょう．

となるので，内積はユニタリー変換に対して不変です．作用素行列の変換式も求めておきましょう．もとの作用素行列，

に対して，基底を変換した場合の新しい作用素行列を，

とします．行列要素は，

から，

へ変換されます．最後の式は次のように計算されます．

故に，変換式が求められました．また，この変換式の両辺に左からを，右からを作用させて計算すると，

となります．
　次に，作用素行列の中で，特に，

の関係を満たす行列を考えましょう．この行列をエルミート作用素行列と言います．エルミート作用素行列に対しては，

の関係式が成立します．ここで，エルミート作用素行列をユニタリー変換してみましょう．

と新しい作用素行列をつくり，転置共役をとり，計算します．

すなわち，

“エルミート作用素行列をユニタリー変換した行列もエルミート作用素行列です．”

という結論が得られます．
　関数の場合と同様に，ベクトル空間の場合も固有値問題を考えることができます．

この方程式を固有方程式，を固有ベクトル，aは一般に複素数の定数で固有値と言います．固有ベクトルはN個あります．固有値は最大でN個ですが，場合によっては１つの固有ベクトルに対して複数の固有値が対
応することがあります．これを縮退と呼ぶのは，関数の場合と同様です．
　ここで，次の定理が成立します．

“エルミート作用素行列の固有値は実数です．”

この定理を証明しましょう．固有方程式，

が成立するものとします．ここで，はエルミート作用素行列なので，

したがって，固有値aは実数です．（証明終．）次に，エルミート作用素行列についての，固有ベクトルの性質について調べましょう．

の関係において，ブラベクトル，ケットベクトルをそれぞれm番目とn番目の固有ベクトルとして，とおき，計算します．

エルミート演算子の固有値は実数なので，

となります．異なる固有状態についての固有値が等しくないとき，すなわち，

の場合，

の関係が成立します．つまり，

”エルミート作用素行列の異なる固有値に属する２つの固有ベクトルは直交します．”

という定理が証明されました．また，固有ベクトルに適当な定数を掛けて規格化することができます．

固有ベクトルがg重に縮退している場合を考えましょう．上の議論は縮退していないことを前提としていましたが，縮退しているときは次のグラム-シュミットの直交化法を使います．いま，

が同じ固有値をもつg重に縮退した固有ベクトルとします．まず，

とおき，

となるように定数aを決めます．次に，

とおき，

の条件より，を決定して，を求めます．さらに，

とおき，同様な議論をします．以下，その繰り返しです．最終的に得られた直交条件を満たす固有ベクトルのダッシュをとります．このように縮退がある場合も必ず直交化することができます．以上の，直交条件と規格化条件をまとめると，

が成立します．すなわち，

“エルミート作用素行列の固有ベクトルの全体は，規格直交系を形成します．”

という重要な性質が判明しました．いままでの議論により，規格直交系を成すベクトルによって任意のベクトルが表されることが理解されます．従って，

“エルミート作用素行列の固有ベクトル全体は，基底ベクトルを張ることができます．”

という結論が得られました．

14.3 量子状態:状態ベクトル（ケットベクトルとブラベクトル）

いままでのChapterで見てきた量子力学は，シュレディンガー方程式を中心とした波動力学と呼ばれる形式でした．波動力学では量子状態は波動関数で，オブザーバブルは演算子で表されました．ここで，前のSectionで取り扱ったN次元複素ベクトル空間をさらに拡張した，無限次元複素ベクトル空間の行列を使って，新たに行列力学という形式の量子力学に書き直してみましょう．ベクトルの大きさのことをノルムと言いますが，ノルムの収束する無限次元複素ベクトル空間のことをヒルベルト空間と言います．行列力学はヒルベルト空間によって記述されます．
量子状態とオブザーバブルという量子力学の２つの基礎概念を，行列を使って表しましょう．まず，量子状態を考えます．波動力学では，完全系である規格直交系によって，量子状態を表す任意の波動関数ψは展開して表されました．