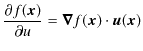J Simplicity オブザーバブル（線形エルミート演算子と期待値・固有値）

Chapter8 オブザーバブル（線形エルミート演算子と期待値・固有値）

8.1 古典的物理量

前のChapterの "量子状態（波動関数と確率振幅）" に引き続き，このChapterでは，量子力学の2つ目の基礎概念を考えていきましょう．その基礎概念は，量子力学的な物理量であるオブザーバブルといいます．（量子力学を構成する基礎概念は，量子状態とオブザーバブルの2つしかありません．）

　このSectionでは，古典論における物理量の意味を確認しておきます．物理量には，座標，運動量，エネルギー，角運動量といったものがありますが，物理量の間の関係を方程式で表し，物理法則を表現することが常套手段です．古典論における物理量というものを，次の3つに分類することができます．

文字式を使って，数学的に表現されるもの．（古典的数学表現）
数学的表現を使い，物理法則を表す方程式から計算によって理論的に予測されるもの．（古典的理論値）
古典的理想装置により，測定されるもの．（古典的理想測定値）

実験すると測定値が得られますが，通常，誤差が生じます．これは実験装置の不備，あるいは人為的な要因によるものです．仮に，完全に誤差を生じない古典的理想装置というものを考えましょう．（このように理想化された思考実験を考えます．）この古典的理想装置による測定値を古典的理想測定値と名付けます．この場合，古典的理想測定値は古典的理論値と常に完全に一致します．古典論は決定論であり，完全に予測可能な理論であることを特徴としていましたね．それでは，量子力学の1形態である波動力学の場合は，どのようになるのでしょうか？次のSection以降で見ていくことにしましょう．

8.2 波動力学的物理量の数学的表現（演算子）

波動力学では物理量とはどのようなものでしょうか？シュレディンガー方程式を導入する際，古典的物理量の間に成立する関係式において，物理量を演算子に置き換える手続きをしたことを思い出して下さい．この手続きを量子化といいましたが，量子化は形式的なものに留まらず，深い意味をもっています．つまり，

　"波動力学における物理量の数学的表現は演算子です．"

ということが，一般に成立するのです．以後，演算子にはハットを付けて，一般に，

$\displaystyle \hat{A}$

と表すことにします．

　例を挙げていきましょう．（"シュレディンガー方程式" のChapterの "量子化" のSectionを参照して下さい．）まず，座標の物理量については，古典的数学表現は $\bm{x}=(x,y,z)$ ですが，波動力学における数学的表現は，古典論のものがそのまま波動力学で適用されました．すなわち，

	$\displaystyle x\to\hat{x}=x$
	$\displaystyle x\to\hat{y}=y$
	$\displaystyle x\to\hat{z}=z$

です．これらを座標演算子といいます．次に，運動量の古典的数学表現は $\bm{p}=(p_{x},p_{y},p_{z})$ ですが，波動力学における数学的表現は，量子化して，

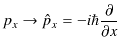	$\displaystyle p_{x}\to\hat{p}_{x}=-i\hbar\dfrac{\partial}{\partial x}$
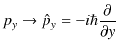	$\displaystyle p_{y}\to\hat{p}_{y}=-i\hbar\dfrac{\partial}{\partial y}$
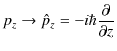	$\displaystyle p_{z}\to\hat{p}_{z}=-i\hbar\dfrac{\partial}{\partial z}$

となります．これらを運動量演算子といいます．また，エネルギーの古典的数学表現はと一文字で表しますが，波動力学における数学的表現は，量子化して，

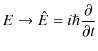
$\displaystyle E\to\hat{E}=i\hbar\dfrac{\partial}{\partial t}$

です．これをエネルギー演算子といいます．最後の例として，角運動量についても考えてみましょう．古典論における数学的表現は，

$\displaystyle \bm{L}\equiv\bm{x}\times\bm{p}$

すなわち，

	$\displaystyle L_{x}=yp_{z}-zp_{y}$
	$\displaystyle L_{y}=zp_{x}-xp_{z}$
	$\displaystyle L_{z}=xp_{y}-yp_{x}$

です．波動力学での数学的表現は，座標を座標演算子に，運動量を運動量演算子に置き換えて量子化します．

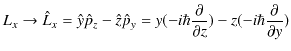	$\displaystyle L_{x}\to\hat{L}_{x}=\hat{y}\hat{p}_{z}-\hat{z}\hat{p}_{y}=y(-i\hbar\dfrac{\partial}{\partial z})-z(-i\hbar\dfrac{\partial}{\partial y})$
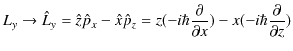	$\displaystyle L_{y}\to\hat{L}_{y}=\hat{z}\hat{p}_{x}-\hat{x}\hat{p}_{z}=z(-i\hbar\dfrac{\partial}{\partial x})-x(-i\hbar\dfrac{\partial}{\partial z})$
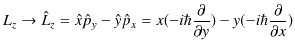	$\displaystyle L_{z}\to\hat{L}_{z}=\hat{x}\hat{p}_{y}-\hat{y}\hat{p}_{x}=x(-i\hbar\dfrac{\partial}{\partial y})-y(-i\hbar\dfrac{\partial}{\partial x})$

すなわち，

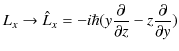	$\displaystyle L_{x}\to\hat{L}_{x}=-i\hbar(y\dfrac{\partial}{\partial z}-z\dfrac{\partial}{\partial y})$
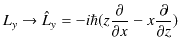	$\displaystyle L_{y}\to\hat{L}_{y}=-i\hbar(z\dfrac{\partial}{\partial x}-x\dfrac{\partial}{\partial z})$
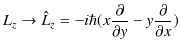	$\displaystyle L_{z}\to\hat{L}_{z}=-i\hbar(x\dfrac{\partial}{\partial y}-y\dfrac{\partial}{\partial x})$

となります．最後の3式が角運動量演算子です．

8.3 交換関係

古典的物理量を表す2つの文字式の間には，掛け算の順序によって結果が異なることはありませんでした．例えば，座標と運動量 $p_{x}$ の積においては，どちらから先に書いてもよいのです．つまり，

$\displaystyle xp_{x}=p_{x}x$

という恒等式が成立します．このように古典的理論では積の順序は意識する必要はないのです．古典的物理量の数学的表現である文字式のことをc-数（cardinal number: 計量数）といいます．

　波動力学を考えましょう．波動力学的物理量の数学的表現は演算子でした．演算子の積の順序に着目しましょう．例えば，座標演算子同士の場合を考えます．演算子は波動関数に作用してはじめて意味があるので，そのようにしておきます．

$\displaystyle \hat{x}\hat{y}\phi(\bm{x})$	$\displaystyle =xy\phi(\bm{x})$
	$\displaystyle =yx\phi(\bm{x})$
	$\displaystyle =\hat{y}\hat{x}\phi(\bm{x})$

特に問題はありません．それでは，座標演算子と運動量演算子の間でどうなるのか確かめてみましょう．

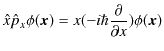
$\displaystyle \hat{x}\hat{p}_{x}\phi(\bm{x})=x(-i\hbar\dfrac{\partial}{\partial x})\phi(\bm{x})$

ですが，一方，

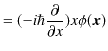$\displaystyle \hat{p}_{x}\hat{x}\phi(\bm{x})$	$\displaystyle =(-i\hbar\dfrac{\partial}{\partial x})x\phi(\bm{x})$
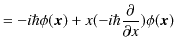	$\displaystyle =-i\hbar\phi(\bm{x})+x(-i\hbar\dfrac{\partial}{\partial x})\phi(\bm{x})$
	$\displaystyle =-i\hbar\phi(\bm{x})+\hat{x}\hat{p}_{x}\phi(\bm{x})$

です．このように，座標演算子と運動量演算子の作用する順番を換えた量は同じにはなりません．古典的物理量の数学的に表現された量とは，全く相違するのです．最後の式をもう少し見やすい形にしていきましょう．移項して，整理していきます．

	$\displaystyle \hat{x}\hat{p}_{x}\phi(\bm{x})-\hat{p}_{x}\hat{x}\phi(\bm{x})=i\hbar\phi(\bm{x})$
$% latex2html id marker 2489 $\displaystyle \therefore$$	$\displaystyle (\hat{x}\hat{p}_{x}-\hat{p}_{x}\hat{x})\phi(\bm{x})=i\hbar\phi(\bm{x})$

ここで，便利な記号である交換子というものを次のように定義します．

$\displaystyle [\hat{A},\hat{B}]\equiv\hat{A}\hat{B}-\hat{B}\hat{A}$

このとき，

$\displaystyle [\hat{x},\hat{p}_{x}]\phi(\bm{x})=i\hbar\phi(\bm{x})$

となります．ここで，波動関数を書かずに，演算子の間だけの関係を記すと，

$\displaystyle [\hat{x},\hat{p}_{x}]=i\hbar$

となります．このような式を交換関係といいます．（演算子だけの関係式ですが，いつも波動関数に作用しているということに気を付けて下さい．交換関係は物理量である演算子の性質を規定するものです．）波動力学では，物理量が演算子で示されるため，その積が交換する場合と交換しない場合があるのです．交換する場合を交換可能（可換），交換しない場合を交換不可能（非可換）といいます．また，交換関係で規定される物理量を表す演算子のことを，q-数（quantum mechanical number）ともいいます．座標演算子と運動量演算子について，上で計算した量以外のものについても，同様に計算ができます．まとめて書いておきます．

	$\displaystyle [\hat{x},\hat{p}_{x}]=[\hat{y},\hat{p}_{y}]=[\hat{z},\hat{p}_{z}]=i\hbar$
	$\displaystyle [\hat{x},\hat{p}_{y}]=[\hat{x},\hat{p}_{z}]=[\hat{y},\hat{p}_{z}]=[\hat{y},\hat{p}_{x} ]=[\hat{z},\hat{p}_{x}]=[\hat{z},\hat{p}_{y}]=0$

　次に，計算が複雑になりますが，角運動量演算子の成分間に成立する交換関係についても取り扱っておきましょう．まず，交換関係に関する恒等式を証明しておきます．

$\displaystyle [\hat{A}\hat{B},\hat{C}]$	$\displaystyle =\hat{A}\hat{B}\hat{C}-\hat{C}\hat{A}\hat{B}$
	$\displaystyle =\hat{A}\hat{B}\hat{C}-\hat{A}\hat{C}\hat{B}+\hat{A}\hat{C}\hat{B}-\hat{C}\hat{A}\hat{B}$
	$\displaystyle =\hat{A}(\hat{B}\hat{C}-\hat{C}\hat{B})+(\hat{A}\hat{C}-\hat{C}\hat{A})\hat{B}$
	$\displaystyle =\hat{A}[\hat{B},\hat{C}]+[\hat{A},\hat{C}]\hat{B}$

と，

$\displaystyle [\hat{A},\hat{B}\hat{C}]$	$\displaystyle =\hat{A}\hat{B}\hat{C}-\hat{B}\hat{C}\hat{A}$
	$\displaystyle =\hat{A}\hat{B}\hat{C}-\hat{B}\hat{A}\hat{C}+\hat{B}\hat{A}\hat{C}-\hat{B}\hat{C}\hat{A}$
	$\displaystyle =(\hat{A}\hat{B}-\hat{B}\hat{A})\hat{C}+\hat{B}(\hat{A}\hat{C}-\hat{C}\hat{A})$
	$\displaystyle =[\hat{A},\hat{B}]\hat{C}+\hat{B}[\hat{A},\hat{C}]$

が成立します．これらの式を使って，次の計算もできます．

$\displaystyle [\hat{A}\hat{B},\hat{C}\hat{D}]$	$\displaystyle =\hat{A}[\hat{B},\hat{C}\hat{D}]+[\hat{A},\hat{C}\hat{D}]\hat{B}$
	$\displaystyle =\hat{A}([\hat{B},\hat{C}]\hat{D}+\hat{C}[\hat{B},\hat{D}])+([\hat{A},\hat{C}]\hat{D}+\hat{C}[\hat{A},\hat{D}])\hat{B}$
	$\displaystyle =\hat{A}[\hat{B},\hat{C}]\hat{D}+\hat{A}\hat{C}[\hat{B},\hat{D}]+[\hat{A},\hat{C}]\hat{D}\hat{B}+\hat{C}[\hat{A},\hat{D}]\hat{B}$

最後の恒等式を使って，次のように計算できます．

$\displaystyle [\hat{L}_{x},\hat{L}_{y}]$	$\displaystyle =[\hat{y}\hat{p}_{z}-z\hat{p}_{y},\hat{z}\hat{p}_{x}-\hat{x}\hat{p}_{z}]$
	$\displaystyle =[\hat{y}\hat{p}_{z},\hat{z}\hat{p}_{x}]-[\hat{y}\hat{p}_{z},\hat... ...[\hat{z}\hat{p}_{y},\hat{z}\hat{p}_{x}]+[\hat{z}\hat{p}_{y},\hat{x}\hat{p}_{z}]$
	$\displaystyle =\hat{y}[\hat{p}_{z},\hat{z}]\hat{p}_{x}+\hat{y}\hat{z}[\hat{p}_{... ...[\hat{y},\hat{z}]\hat{p}_{x}\hat{p}_{z}+\hat{z}[\hat{y},\hat{p}_{x}]\hat{p}_{z}$
	$\displaystyle \,\,\,-(\hat{y}[\hat{p}_{z},\hat{x}]\hat{p}_{z}+\hat{y}\hat{x}[\h... ...+[\hat{y},\hat{x}]\hat{p}_{z}\hat{p}_{z}+\hat{x}[\hat{y},\hat{p}_{z}]\hat{p}_z)$
	$\displaystyle \,\,\,-(\hat{z}[\hat{p}_{y},\hat{z}]\hat{p}_{x}+\hat{z}\hat{z}[\h... ...\hat{z},\hat{z}]\hat{p}_{x}\hat{p}_{y}+\hat{z}[\hat{z},\hat{p}_{x}]\hat{p}_{y})$
	$\displaystyle \,\,\,+\hat{z}[\hat{p}_{y},\hat{x}]\hat{p}_{z}+\hat{z}\hat{x}[\ha... ...[\hat{z},\hat{x}]\hat{p}_{z}\hat{p}_{y}+\hat{x}[\hat{z},\hat{p}_{z}]\hat{p}_{y}$
	$\displaystyle =\hat{y}(-i\hbar)\hat{p}_{x}+\hat{y}\hat{z}\cdot0+0\cdot\hat{p}_{... ...{y}\hat{x}\cdot0+0\cdot\hat{p}_{z}\hat{p}_{z}+\hat{x}\cdot0\cdot\hat{p} ̂_{z})$
	$\displaystyle \,\,\,-(\hat{z}\cdot0\cdot\hat{p}_{x}+\hat{z}\hat{z}\cdot0+0\cdot... ...z}+\hat{z}\hat{x}\cdot0+0\cdot\hat{p}_{z}\hat{p}_{y}+\hat{x}(i\hbar)\hat{p}_{y}$
	$\displaystyle =i\hbar(\hat{x}\hat{p}_{y}-\hat{y}\hat{p}_{x})$
	$\displaystyle =i\hbar\hat{L}_{z}$

故に，

$\displaystyle [\hat{L}_{x},\hat{L}_{y}]=i\hbar\hat{L}_{z}$

が成立します．他の角運動量の成分間の交換関係も同様に計算することができます．その結果をここでまとめておきます．

	$\displaystyle [\hat{L}_{x},\hat{L}_{y}]=i\hbar\hat{L}_{z}$
	$\displaystyle [\hat{L}_{y},\hat{L}_{z}]=i\hbar\hat{L}_{x}$
	$\displaystyle [\hat{L}_{z},\hat{L}_{x}]=i\hbar\hat{L}_{y}$

　波動力学において，物理量の数学的表現が演算子であることについて考えてきました．それでは，演算子から物理量の理論値はどのように計算されるのでしょうか？また，理論値と測定値はどのように関係しているのでしょうか？次のSectionで数学的準備をして，それ以降のSectionで考えていくことにしましょう．

8.4 数学的準備（グリーンの定理）

このSectionでは，数学的準備として，グリーンの定理というものを証明しておきます．グリーンの定理とは，

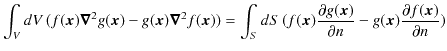
$\displaystyle \int_{V}dV\,(f(\bm{x})\bm{\nabla}^{2}g(\bm{x})-g(\bm{x})\bm{\nabl... ...partial g(\bm{x})}{\partial n}-g(\bm{x})\dfrac{\partial f(\bm{x})}{\partial n})$

という式で表される定理です．（左辺は体積分で，

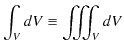
$\displaystyle \int_{V}dV\equiv\iiint_{V}dV$

であり，右辺は面積分で，

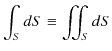
$\displaystyle \int_{S}dS\equiv\iint_{S}dS$

です．右辺の $\partial f(\bm{x})/\partial n$ と $\partial g(\bm{x})/\partial n$ は面積分する表面の法線（ $\bm{n}(\bm{x})$ ベクトル）方向への方向微分とよばれる量です．このあとすぐ説明します．）

　まず最初に，方向微分という量を導入します．デカルト座標の上で，点 $P(\bm{x})$ をとり，点 $P(\bm{x})$ のごく近傍の点を考えます．そして， $\overrightarrow{PQ}$ の方向を単位ベクトル $\bm{u}(\bm{x})=(\ell,m,n)$ で表します．（ $(\ell,m,n)$ は方向余弦になっています．）また， $\overrightarrow{PQ}$ の大きさ，つまり， $\overrightarrow{PQ}$ の距離をとすれば，

$\displaystyle \overrightarrow{PQ}=s\bm{u}(\bm{x})$

となります．よって，の座標は，

$\displaystyle \bm{x}+\overrightarrow{PQ}$	$\displaystyle =\bm{x}+s\bm{u}(\bm{x})$
	$\displaystyle =(x+\ell s,y+ms,z+ns)$

と表されます．ここで， $\bm{u}(\bm{x})$ は一定にしておき，を 0 に近づけた場合， $Q\to P$ になりますが，このときのスカラー場 $f(\bm{x})$ の変化の割合を考えましょう．すなわち，

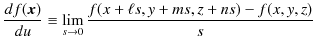
$\displaystyle \dfrac{df(\bm{x})}{du}\equiv\lim_{s\to0}\dfrac{f(x+\ell s,y+ms,z+ns)-f(x,y,z)}{s}$

という量を考えます．この式で定義される，スカラー場 $f(\bm{x})$ の $\bm{u}(\bm{x})$ 方向への変化の割合を方向微分といいます．（記号の定義方法として， $df(\bm{x})/ds$ と約束した方が意味の上からは正しいのかもしれません．実際，このように定義することもあります．しかし，ここでは，上記のように $df(\bm{x})/du$ と書くように約束しておきます．）方向微分を表す式を求めておきましょう．右辺をテイラー展開して計算します．

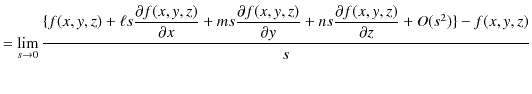$\displaystyle \dfrac{df(\bm{x})}{du}$	$\displaystyle =\lim_{s\to0}\dfrac{\{f(x,y,z)+\ell s\dfrac{\partial f(x,y,z)}{\p... ...z)}{\partial y}+ns\dfrac{\partial f(x,y,z)}{\partial z}+O(s^{2})\}-f(x,y,z)}{s}$
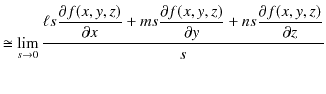	$\displaystyle \cong\lim_{s\to0}\dfrac{\ell s\dfrac{\partial f(x,y,z)}{\partial ... ...frac{\partial f(x,y,z)}{\partial y}+ns\dfrac{\partial f(x,y,z)}{\partial z}}{s}$
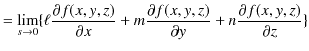	$\displaystyle =\lim_{s\to0}\{\ell\dfrac{\partial f(x,y,z)}{\partial x}+m\dfrac{\partial f(x,y,z)}{\partial y}+n\dfrac{\partial f(x,y,z)}{\partial z}\}$
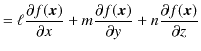	$\displaystyle =\ell\dfrac{\partial f(\bm{x})}{\partial x}+m\dfrac{\partial f(\bm{x})}{\partial y}+n\dfrac{\partial f(\bm{x})}{\partial z}$
	$\displaystyle =\bm{\nabla}f(\bm{x})\cdot\bm{u}(\bm{x})$

この結果は，偏微分の記号を使って，

$\displaystyle \dfrac{\partial f(\bm{x})}{\partial u}=\bm{\nabla}f(\bm{x})\cdot\bm{u}(\bm{x})$

(8.1)

と表す場合が多くみられます．

　それでは，グリーンの定理を証明します．ガウスの定理，

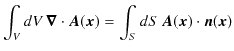
$\displaystyle \int_{V}dV\,\bm{\nabla}\cdot\bm{A}(\bm{x})=\int_{S}dS\,\bm{A}(\bm{x})\cdot\bm{n}(\bm{x})$

において，ベクトル $\bm{A}(\bm{x})$ を，

$\displaystyle \bm{A}(\bm{x})=f(\bm{x})\bm{\nabla}g(\bm{x})-g(\bm{x})\bm{\nabla}f(\bm{x})$

ととってみます． $f(\bm{x})$ と $g(\bm{x})$ は，任意のスカラー場です．このとき，

$\displaystyle \bm{\nabla}\cdot\bm{A}(\bm{x})$	$\displaystyle =\bm{\nabla}\cdot(f(\bm{x})\bm{\nabla}g(\bm{x})-g(\bm{x})\bm{\nabla}f(\bm{x}))$
	$\displaystyle =\bm{\nabla}f(\bm{x})\cdot\bm{\nabla}g(\bm{x})+f(\bm{x})\bm{\nabl... ...\bm{\nabla}g(\bm{x})\cdot\bm{\nabla}f(\bm{x})-g(\bm{x})\bm{\nabla}^{2}f(\bm{x})$
	$\displaystyle =f(\bm{x})\bm{\nabla}^{2}g(\bm{x})-g(\bm{x})\bm{\nabla}^{2}f(\bm{x})$

であり，

$\displaystyle \bm{A}(\bm{x})\cdot\bm{n}(\bm{x})$	$\displaystyle =(f(\bm{x})\bm{\nabla}g(\bm{x})-g(\bm{x})\bm{\nabla}f(\bm{x}))\cdot\bm{n}(\bm{x})$
	$\displaystyle =f(\bm{x})\bm{\nabla}g(\bm{x})\cdot\bm{n}(\bm{x})-g(\bm{x})\bm{\nabla}f(\bm{x})\cdot\bm{n}(\bm{x})$
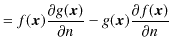	$\displaystyle =f(\bm{x})\dfrac{\partial g(\bm{x})}{\partial n}-g(\bm{x})\dfrac{\partial f(\bm{x})}{\partial n}$

となります．最後の変形には，方向微分の式である(8.1)式を使いました．これらの式を，ガウスの定理に代入すると，

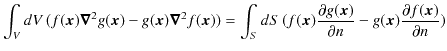
$\displaystyle \int_{V}dV\,(f(\bm{x})\bm{\nabla}^{2}g(\bm{x})-g(\bm{x})\bm{\nabl... ...partial g(\bm{x})}{\partial n}-g(\bm{x})\dfrac{\partial f(\bm{x})}{\partial n})$

となります．（証明終．）

8.5 波動力学的理想測定値の平均値（期待値）

このChapterの最初のSectionで古典的物理量を考えた場合，古典的理論値と古典的理想測定値は，常に完全に一致し，決定論的に予測することができることを説明しました．波動力学の場合を考えてみましょう．古典論の説明のときと同様に，思考実験をしていきます．まず，完全に誤差のない実験装置を想定します．これを波動力学的理想装置と名付けます．そして，そのときの測定値を波動力学的理想測定値とします．複数回の実験をして，複数の理想測定値のデータを採ったとしましょう．このとき，波動力学に従うと，測定値の結果にはバラツキが生じます．（理想的な思考実験なので，装置の不備，あるいは人為的な誤差は完全に 0 のはずです．）残念ながら，波動力学では1つの決定論的な理論値を計算することは不可能なのです．ここで，波動力学は本質的に確率の理論であることを強調しておきましょう．実験する前から，1つの確定値を得ることはできませんが，確率的に理論値を求めることができます．このSectionでは，バラツキのある波動力学的理想測定値の平均値に，完全に一致する理論値（これを期待値といいます．）を求める方法を見ていきましょう．

　一般に，物理量の期待値を次のように表します．

$\displaystyle \langle\hat{A}\rangle$

具体的に期待値を表す式を求めていきます．まず，座標の期待値 $\langle\hat{\bm{x}}\rangle$ を求めましょう．粒子の存在確率密度が，

$\displaystyle \rho(t,\bm{x})$	$\displaystyle =\vert\psi(t,\bm{x})\vert^{2}$
	$\displaystyle =\psi^{*}(t,\bm{x})\psi(t,\bm{x})$

であったことを考慮して，

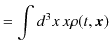$\displaystyle \langle\hat{x}\rangle$	$\displaystyle =\int d^{3}x\,x\rho(t,\bm{x})$
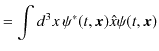	$\displaystyle =\int d^{3}x\,\psi^{*}(t,\bm{x})\hat{x}\psi(t,\bm{x})$

となります．ここで，3次元の積分記号は，

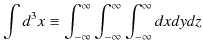
$\displaystyle \int d^{3}x\equiv\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}dxdydz$

と約束していましたね．粒子は全空間で存在する確率がありますので，積分範囲はこのようにとります．同様にして，

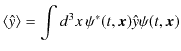	$\displaystyle \langle\hat{y}\rangle=\int d^{3}x\,\psi^{*}(t,\bm{x})\hat{y}\psi(t,\bm{x})$
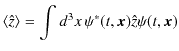	$\displaystyle \langle\hat{z}\rangle=\int d^{3}x\,\psi^{*}(t,\bm{x})\hat{z}\psi(t,\bm{x})$

となります．これら3式をまとめて書くと，

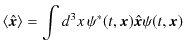
$\displaystyle \langle\hat{\bm{x}}\rangle=\int d^{3}x\,\psi^{*}(t,\bm{x})\hat{\bm{x}}\psi(t,\bm{x})$

となります．

　次に，運動量の期待値を求めます．準備として， $\langle\hat{x}\rangle$ の時間微分を求めます．これは古典論での速度に対応する量であると考えられます．

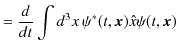$\displaystyle \dfrac{d}{dt}\langle\hat{x}\rangle$	$\displaystyle =\dfrac{d}{dt}\int d^{3}x\,\psi^{*}(t,\bm{x})\hat{x}\psi(t,\bm{x})$
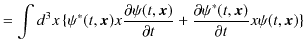	$\displaystyle =\int d^{3}x\,\{\psi^{}(t,\bm{x})x\dfrac{\partial\psi(t,\bm{x})}{\partial t}+\dfrac{\partial\psi^{}(t,\bm{x})}{\partial t}x\psi(t,\bm{x})\}$

となります．ここで，シュレディンガー方程式，

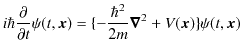
$\displaystyle i\hbar\dfrac{\partial}{\partial t}\psi(t,\bm{x})=\{-\dfrac{\hbar^{2}}{2m}\bm{\nabla}^{2}+V(\bm{x})\}\psi(t,\bm{x})$

より，

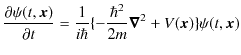
$\displaystyle \dfrac{\partial\psi(t,\bm{x})}{\partial t}=\dfrac{1}{i\hbar}\{-\dfrac{\hbar^{2}}{2m}\bm{\nabla}^{2}+V(\bm{x})\}\psi(t,\bm{x})$

が成り立ちます．この式の複素共役をとると，

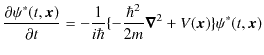
$\displaystyle \dfrac{\partial\psi^{*}(t,\bm{x})}{\partial t}=-\dfrac{1}{i\hbar}\{-\dfrac{\hbar^{2}}{2m}\bm{\nabla}^{2}+V(\bm{x})\}\psi^{*}(t,\bm{x})$

となります．ただし，ポテンシャルは実数と仮定しました．（ $V^{*}(\bm{x})=V(\bm{x})$ ）これらの式を上式に代入して計算します．

$\displaystyle \dfrac{d}{dt}\langle\hat{x}\rangle$	$\displaystyle =\int d^{3}x\,[\psi^{}(t,\bm{x})x\{\dfrac{1}{i\hbar}(-\dfrac{\hb... ...ac{\hbar^{2}}{2m}\bm{\nabla}^{2}+V(\bm{x}))\psi^{}(t,\bm{x})\}x\psi(t,\bm{x})]$
	$\displaystyle =\dfrac{\hbar}{2mi}\int d^{3}x\,[-\psi^{}(t,\bm{x})x\{\bm{\nabla}^{2}\psi(t,\bm{x})\}+x\psi(t,\bm{x})\{\bm{\nabla}^{2}\psi^{}(t,\bm{x})\}]$

となります．ここで，準備しておいたグリーンの定理，

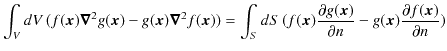
$\displaystyle \int_{V}dV\,(f(\bm{x})\bm{\nabla}^{2}g(\bm{x})-g(\bm{x})\bm{\nabl... ...partial g(\bm{x})}{\partial n}-g(\bm{x})\dfrac{\partial f(\bm{x})}{\partial n})$

使います．このとき， $f=x\psi(t,\bm{x}),g=\psi^{*}(t,\bm{x})$ とおいて，

$\displaystyle \int_{V}dV\,[x\psi(t,\bm{x})\bm{\nabla}^{2}\psi^{*}(t,\bm{x})-\ps... ...{\partial n}-\psi^{*}(t,\bm{x})\dfrac{\partial\{x\psi(t,\bm{x})\}}{\partial n}]$

が確かめられます．ここで， $\psi(t,\bm{x})$ は $\vert\bm{x}\vert^{-2}$ に比例して減衰していくと仮定します．波動関数が局在した状態である波束を形成しているときは，この条件は満たされると考えられます．面積分の表面は無限遠にありますので，仮定が成立するとき，右辺の値は 0 になります．（右辺の非積分関数第1項 $x\psi(t,\bm{x})$ において，は無限大になりますが， $\psi(t,\bm{x})$ が $\vert\bm{x}\vert^{-2}$ に比例して減衰すれば，この項も 0 になりますね．）故に，

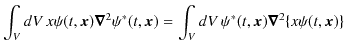
$\displaystyle \int_{V}dV\,x\psi(t,\bm{x})\bm{\nabla}^{2}\psi^{*}(t,\bm{x})=\int_{V}dV\,\psi^{*}(t,\bm{x})\bm{\nabla}^{2}\{x\psi(t,\bm{x})\}$

ですから，

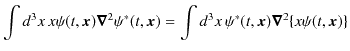
$\displaystyle \int d^{3}x\,x\psi(t,\bm{x})\bm{\nabla}^{2}\psi^{*}(t,\bm{x})=\int d^{3}x\,\psi^{*}(t,\bm{x})\bm{\nabla}^{2}\{x\psi(t,\bm{x})\}$

となります．したがって，

$\displaystyle \dfrac{d}{dt}\langle\hat{x}\rangle$	$\displaystyle =\dfrac{\hbar}{2mi}\int d^{3}x\,[-\psi^{}(t,\bm{x})x\{\bm{\nabla}^{2}\psi(t,\bm{x})\}+x\psi(t,\bm{x})\{\bm{\nabla}^{2}\psi^{}(t,\bm{x})\}]$
	$\displaystyle =\dfrac{\hbar}{2mi}\int d^{3}x\,[-\psi^{}(t,\bm{x})x\{\bm{\nabla}^{2}\psi(t,\bm{x})\}+\psi^{}(t,\bm{x})\bm{\nabla}^{2}\{x\psi(t,\bm{x})\}]$

となります．最後の式の被積分第2項で，

$\displaystyle \bm{\nabla}^{2}\{x\psi(t,\bm{x})\}$	$\displaystyle =\bm{\nabla}\cdot(\bm{\nabla}x\cdot\psi(t,\bm{x})+x\bm{\nabla}\psi(t,\bm{x}))$
	$\displaystyle =\bm{\nabla}^{2}x\cdot\psi(t,\bm{x})+2\bm{\nabla}x\cdot\bm{\nabla}\psi(t,\bm{x})+x\bm{\nabla}^{2}\psi(t,\bm{x})$
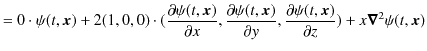	$\displaystyle =0\cdot\psi(t,\bm{x})+2(1,0,0)\cdot(\dfrac{\partial\psi(t,\bm{x})... ...l y},\dfrac{\partial\psi(t,\bm{x})}{\partial z})+x\bm{\nabla}^{2}\psi(t,\bm{x})$
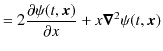	$\displaystyle =2\dfrac{\partial\psi(t,\bm{x})}{\partial x}+x\bm{\nabla}^{2}\psi(t,\bm{x})$

となりますので，

$\displaystyle \dfrac{d}{dt}\langle\hat{x}\rangle$	$\displaystyle =\dfrac{\hbar}{2mi}\int d^{3}x\,[-\psi^{*}(t,\bm{x})x\{\bm{\nabla... ...\{2\dfrac{\partial\psi(t,\bm{x})}{\partial x}+x\bm{\nabla}^{2}\psi(t,\bm{x})\}]$
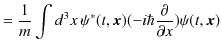	$\displaystyle =\dfrac{1}{m}\int d^{3}x\,\psi^{*}(t,\bm{x})(-i\hbar\dfrac{\partial}{\partial x})\psi(t,\bm{x})$

と変形できます．故に，運動量の成分の期待値は，

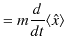$\displaystyle \langle\hat{p}_{x}\rangle$	$\displaystyle =m\dfrac{d}{dt}\langle\hat{x}\rangle$
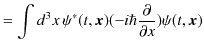	$\displaystyle =\int d^{3}x\,\psi^{*}(t,\bm{x})(-i\hbar\dfrac{\partial}{\partial x})\psi(t,\bm{x})$
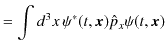	$\displaystyle =\int d^{3}x\,\psi^{*}(t,\bm{x})\hat{p}_{x}\psi(t,\bm{x})$

と求められます．成分と成分も同様にして，

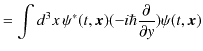$\displaystyle \langle\hat{p}_{y}\rangle$	$\displaystyle =\int d^{3}x\,\psi^{*}(t,\bm{x})(-i\hbar\dfrac{\partial}{\partial y})\psi(t,\bm{x})$
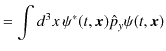	$\displaystyle =\int d^{3}x\,\psi^{*}(t,\bm{x})\hat{p}_{y}\psi(t,\bm{x})$
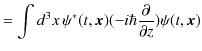$\displaystyle \langle\hat{p}_{z}\rangle$	$\displaystyle =\int d^{3}x\,\psi^{*}(t,\bm{x})(-i\hbar\dfrac{\partial}{\partial z})\psi(t,\bm{x})$
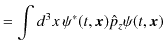	$\displaystyle =\int d^{3}x\,\psi^{*}(t,\bm{x})\hat{p}_{z}\psi(t,\bm{x})$

となります．まとめて書くと，

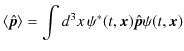
$\displaystyle \langle\hat{\bm{p}}\rangle=\int d^{3}x\,\psi^{*}(t,\bm{x})\hat{\bm{p}}\psi(t,\bm{x})$

と表すことができます．

　以上，座標と運動量の期待値を表す式を導きましたが，一般に波動力学においては，物理量の期待値 $\langle\hat{A}\rangle$ は，物理量の数学的表現である演算子 $\hat{A}$ を用いて，

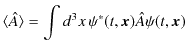
$\displaystyle \langle\hat{A}\rangle=\int d^{3}x\,\psi^{*}(t,\bm{x})\hat{A}\psi(t,\bm{x})$

で与えられるのです．

8.6 エーレンフェストの定理

波動力学では平均の物理量を表す期待値を取り扱えることがわかりました．それではミクロ世界を記述する波動力学とニュートン力学との関係を見ていきましょう．波動力学は20世紀初頭，革新的な理論でしたが，ニュートン力学を全面的に否定するのではなく，それを古典的・マクロ的な極限として含んでいる理論であることを確認していきます．前Sectionで得た運動量の成分の期待値を表す式，

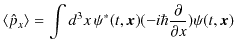
$\displaystyle \langle\hat{p}_{x}\rangle=\int d^{3}x\,\psi^{*}(t,\bm{x})(-i\hbar\dfrac{\partial}{\partial x})\psi(t,\bm{x})$

を時間で微分します．

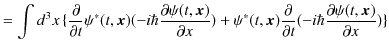$\displaystyle \dfrac{d}{dt}\langle\hat{p}_{x}\rangle$	$\displaystyle =\int d^{3}x\,\{\dfrac{\partial}{\partial t}\psi^{*}(t,\bm{x})(-i... ...frac{\partial}{\partial t}(-i\hbar\dfrac{\partial\psi(t,\bm{x})}{\partial x})\}$
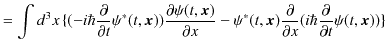	$\displaystyle =\int d^{3}x\,\{(-i\hbar\dfrac{\partial}{\partial t}\psi^{*}(t,\b... ...dfrac{\partial}{\partial x}(i\hbar\dfrac{\partial}{\partial t}\psi(t,\bm{x}))\}$

ここで，シュレディンガー方程式，

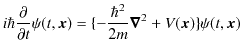
$\displaystyle i\hbar\dfrac{\partial}{\partial t}\psi(t,\bm{x})=\{-\dfrac{\hbar^{2}}{2m}\bm{\nabla}^{2}+V(\bm{x})\}\psi(t,\bm{x})$

と，その複素共役をとった式，

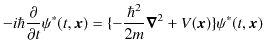
$\displaystyle -i\hbar\dfrac{\partial}{\partial t}\psi^{*}(t,\bm{x})=\{-\dfrac{\hbar^{2}}{2m}\bm{\nabla}^{2}+V(\bm{x})\}\psi^{*}(t,\bm{x})$

を代入して計算します．ただし，ポテンシャルは実数と仮定しました．（ $V^{*}(\bm{x})=V(\bm{x})$ ）

$\displaystyle \dfrac{d}{dt}\langle\hat{p}_{x}\rangle$	$\displaystyle =\int d^{3}x\,[\{(-\dfrac{\hbar^{2}}{2m}\bm{\nabla}^{2}+V(\bm{x})... ...al}{\partial x}(-\dfrac{\hbar^{2}}{2m}\bm{\nabla}^{2}+V(\bm{x}))\psi(t,\bm{x})]$
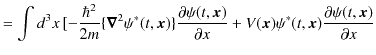	$\displaystyle =\int d^{3}x\,[-\dfrac{\hbar^{2}}{2m}\{\bm{\nabla}^{2}\psi^{}(t,... ...artial x}+V(\bm{x})\psi^{}(t,\bm{x})\dfrac{\partial\psi(t,\bm{x})}{\partial x}$
	$\displaystyle \,\,\,+\dfrac{\hbar^{2}}{2m}\psi^{}(t,\bm{x})\dfrac{\partial}{\p... ...,\bm{x})-\psi^{}(t,\bm{x})V(\bm{x})\dfrac{\partial\psi(t,\bm{x})}{\partial x}]$
	$\displaystyle =-\dfrac{\hbar^{2}}{2m}\int d^{3}x\,[\dfrac{\partial\psi(t,\bm{x}... ...psi^{*}(t,\bm{x})\bm{\nabla}^{2}\{\dfrac{\partial\psi(t,\bm{x})}{\partial x}\}]$
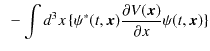	$\displaystyle \,\,\,-\int d^{3}x\,\{\psi^{*}(t,\bm{x})\dfrac{\partial V(\bm{x})}{\partial x}\psi(t,\bm{x})\}$

ここで，ベクトル解析のグリーンの定理，

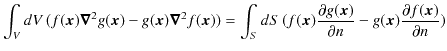
$\displaystyle \int_{V}dV\,(f(\bm{x})\bm{\nabla}^{2}g(\bm{x})-g(\bm{x})\bm{\nabl... ...partial g(\bm{x})}{\partial n}-g(\bm{x})\dfrac{\partial f(\bm{x})}{\partial n})$

を使います．

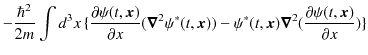	$\displaystyle -\dfrac{\hbar^{2}}{2m}\int d^{3}x\,\{\dfrac{\partial\psi(t,\bm{x}... ...\psi^{*}(t,\bm{x})\bm{\nabla}^{2}(\dfrac{\partial\psi(t,\bm{x})}{\partial x})\}$
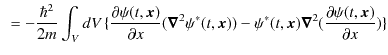	$\displaystyle \,\,\,=-\dfrac{\hbar^{2}}{2m}\int_{V}dV\,\{\dfrac{\partial\psi(t,... ...\psi^{*}(t,\bm{x})\bm{\nabla}^{2}(\dfrac{\partial\psi(t,\bm{x})}{\partial x})\}$
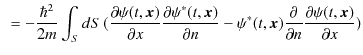	$\displaystyle \,\,\,=-\dfrac{\hbar^{2}}{2m}\int_{S}dS\,(\dfrac{\partial\psi(t,\... ...,\bm{x})\dfrac{\partial}{\partial n}\dfrac{\partial\psi(t,\bm{x})}{\partial x})$

前Sectionと同様に，右辺の面積分の表面は無限遠にありますが，そこで， $\psi(t,\bm{x})$ は 0 になります．（波動関数が波束を形成しているときは，この条件は問題なく満たされます．）したがって，この式の値は 0 です．故に，

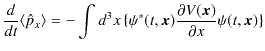	$\displaystyle \dfrac{d}{dt}\langle\hat{p}_{x}\rangle=-\int d^{3}x\,\{\psi^{*}(t,\bm{x})\dfrac{\partial V(\bm{x})}{\partial x}\psi(t,\bm{x})\}$
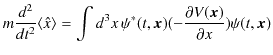$% latex2html id marker 2737 $\displaystyle \therefore$$	$\displaystyle m\dfrac{d^{2}}{dt^{2}}\langle\hat{x}\rangle=\int d^{3}x\,\psi^{*}(t,\bm{x})(-\dfrac{\partial V(\bm{x})}{\partial x})\psi(t,\bm{x})$
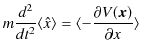$% latex2html id marker 2739 $\displaystyle \therefore$$	$\displaystyle m\dfrac{d^{2}}{dt^{2}}\langle\hat{x}\rangle=\langle-\dfrac{\partial V(\bm{x})}{\partial x}\rangle$

となります．また，成分と成分も同様な計算により，

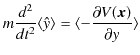	$\displaystyle m\dfrac{d^{2}}{dt^{2}}\langle\hat{y}\rangle=\langle-\dfrac{\partial V(\bm{x})}{\partial y}\rangle$
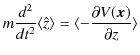	$\displaystyle m\dfrac{d^{2}}{dt^{2}}\langle\hat{z}\rangle=\langle-\dfrac{\partial V(\bm{x})}{\partial z}\rangle$

が求められます．まとめて書くと，

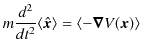
$\displaystyle m\dfrac{d^{2}}{dt^{2}}\langle\hat{\bm{x}}\rangle=\langle-\bm{\nabla}V(\bm{x})\rangle$

が成立します．これはニュートン力学の中核的方程式である運動方程式を波動力学的に表していると考えられます．つまり，量子が良い近似で局在していて，確率を表す波動関数が波束を形成しているとき，その波束の運動が運動方程式に従うということです．これをエーレンフェストの定理といいます．波動力学は，量子が局在しているという極限でニュートン力学を含んでいることになり，理論上望ましい条件を満たしているということが言えるのです．

8.7 波動力学的物理量の数学的表現（線形エルミート演算子）

波動力学においては，物理量の数学的表現は演算子であることを確認しました．ここでは特に，波動力学における演算子の性質について考えておくことにしましょう．一般に，演算子 $\hat{A}$ が，

$\displaystyle \hat{A}(c_{1}\psi_{1}(t,\bm{x})+c_{2}\psi_{2}(t,\bm{x})+\cdots)=c_{1}\hat{A}\psi_{1}(t,\bm{x})+c_{2}\hat{A}\psi_{2}(t,\bm{x})+\cdots$

という関係を満たしているとき， $\hat{A}$ は線形演算子と言います．（ただし， $c_{n}$ は定数， $\psi_{n}(t,\bm{x})$ は $\hat{A}$ が作用する関数です．）例えば，座標演算子は線形演算子です．実際に，次のように確かめられます．

$\displaystyle \hat{x}(c_{1}\psi_{1}(t,\bm{x})+c_{2}\psi_{2}(t,\bm{x})+\cdots)$	$\displaystyle =x(c_{1}\psi_{1}(t,\bm{x})+c_{2}\psi_{2}(t,\bm{x})+\cdots)$
	$\displaystyle =c_{1}x\psi_{1}(t,\bm{x})+c_{2}x\psi_{2}(t,\bm{x})+\cdots$
	$\displaystyle =c_{1}\hat{x}\psi_{1}(t,\bm{x})+c_{2}\hat{x}\psi_{2}(t,\bm{x})+\cdots$

同様に，運動量演算子は線形演算子です．

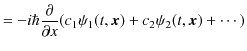$\displaystyle \hat{p}_{x}(c_{1}\psi_{1}(t,\bm{x})+c_{2}\psi_{2}(t,\bm{x})+\cdots)$	$\displaystyle =-i\hbar\dfrac{\partial}{\partial x}(c_{1}\psi_{1}(t,\bm{x})+c_{2}\psi_{2}(t,\bm{x})+\cdots)$
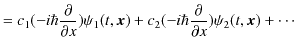	$\displaystyle =c_{1}(-i\hbar\dfrac{\partial}{\partial x})\psi_{1}(t,\bm{x})+c_{2}(-i\hbar\dfrac{\partial}{\partial x})\psi_{2}(t,\bm{x})+\cdots$
	$\displaystyle =c_{1}\hat{p}_{x}\psi_{1}(t,\bm{x})+c_{2}\hat{p}_{x}\psi_{2}(t,\bm{x})+\cdots$

また，波動関数についての重ね合わせの原理を，シュレディンガー方程式を使って確認した際，エネルギー演算子とハミルトニアン演算子の線形性を使ったことも思い出して下さい．（"量子状態（波動関数と確率振幅）" のChapterを参照して下さい．）一般に，波動力学での物理量を表す演算子は線形演算子であることが要請されます．

　前Sectionで見たように，物理量の平均値に対応する期待値は，一般に，

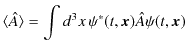
$\displaystyle \langle\hat{A}\rangle=\int d^{3}x\,\psi^{*}(t,\bm{x})\hat{A}\psi(t,\bm{x})$

で与えられます．ここで，複素共役をとると，

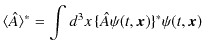
$\displaystyle \langle\hat{A}\rangle^{*}=\int d^{3}x\,\{\hat{A}\psi(t,\bm{x})\}^{*}\psi(t,\bm{x})$

となります．期待値は理想測定値の平均値であるので，実数であることが要請されます．したがって，

$\displaystyle \langle\hat{A}\rangle^{*}=\langle\hat{A}\rangle$

より，

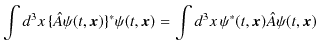
$\displaystyle \int d^{3}x\,\{\hat{A}\psi(t,\bm{x})\}^{*}\psi(t,\bm{x})=\int d^{3}x\,\psi^{*}(t,\bm{x})\hat{A}\psi(t,\bm{x})$

の式が成立します．この関係式を満たす演算子 $\hat{A}$ をエルミート演算子といいます．このようにエルミート演算子は，実数の概念を演算子に拡張したものであるということがいえます．波動力学での物理量の数学的表現である演算子はエルミート演算子であることが要請されます．物理量がエルミート演算子で数学的に表現されていれば，その期待値は実数であることが保証されるのです．

　エルミート演算子のより一般的な定義を述べておきます．任意の演算子 $\hat{A}$ が任意の $\psi_{1}(t,\bm{x}),\psi_{2}(t,\bm{x})$ に対して，

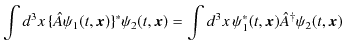
$\displaystyle \int d^{3}x\,\{\hat{A}\psi_{1}(t,\bm{x})\}^{*}\psi_{2}(t,\bm{x})=\int d^{3}x\,\psi_{1}^{*}(t,\bm{x})\hat{A}^{\dagger}\psi_{2}(t,\bm{x})$

を満たすとき， $\hat{A}^{\dagger}$ を $\hat{A}$ に対するエルミート共役演算子といいます．特に，

$\displaystyle \hat{A}^{\dagger}=\hat{A}$

のとき，つまり自己共役の場合， $\hat{A}$ を一般的なエルミート演算子といいます．このとき，

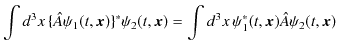
$\displaystyle \int d^{3}x\,\{\hat{A}\psi_{1}(t,\bm{x})\}^{*}\psi_{2}(t,\bm{x})=\int d^{3}x\,\psi_{1}^{*}(t,\bm{x})\hat{A}\psi_{2}(t,\bm{x})$

が成立します．ここで， $\psi_{1}(t,\bm{x})=\psi_{2}(t,\bm{x})=\psi(t,\bm{x})$ とおくと，

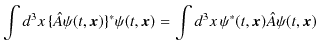
$\displaystyle \int d^{3}x\,\{\hat{A}\psi(t,\bm{x})\}^{*}\psi(t,\bm{x})=\int d^{3}x\,\psi^{*}(t,\bm{x})\hat{A}\psi(t,\bm{x})$

となり，最初のエルミート演算子の定義と一致することが確かめられます．

　波動力学においては，物理量の数学的表現である演算子について，

　"波動力学での物理量を表す演算子は線形エルミート演算子です．"

ということが，基本的事項として要請されます．概念の発展の繋がりは，

　"古典的物理量→波動力学的物理量の数学表現（線形エルミート演算子）"

と表記されます．

8.8 波動力学的理想測定値の個別値（固有値）

波動力学的理想装置の理想測定値の平均値である期待値の求め方については，前述しました．それでは，バラツキのある理想測定値の1つ1つの個別値に一致する波動力学的理論値を求める方法について考えましょう．

　古典論において，理想的でない誤差の生じる装置で実験した場合，測定値と決定論的に決まる真の値の間の誤差 $\Delta A$ は，

$\displaystyle \Delta A\equiv a-A$

と表せます．この場合の $\Delta A$ は実験装置の不備あるいは人為的な要因によるものです．この式を参考にして，波動力学の場合を考えましょう．思考実験をしますが，誤差の生じない波動力学的理想装置で測定すると，測定値にはバラツキが生じます．これは実験装置の不備あるいは人為的なものではなく，波動力学の確率的性質によるものです．上の古典論での誤差の式を参考にして，波動力学における，

$\displaystyle \hat{\Delta A}\equiv\hat{A}-\langle\hat{A}\rangle$

という演算子を導入します． $\hat{A}$ は物理量を表すエルミート演算子であり， $\langle\hat{A}\rangle$ は期待値なので実数です．したがって， $\hat{\Delta A}$ はエルミート演算子になります．エルミート演算子 $\hat{\Delta A}$ は，バラツキのある理想測定値とその平均値である期待値との差に関係する演算子であるということがいえます．この演算子 $\hat{\Delta A}$ の期待値をとると，

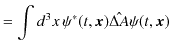$\displaystyle \langle\hat{\Delta A}\rangle$	$\displaystyle =\int d^{3}x\,\psi^{*}(t,\bm{x})\hat{\Delta A}\psi(t,\bm{x})$
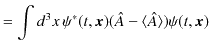	$\displaystyle =\int d^{3}x\,\psi^{*}(t,\bm{x})(\hat{A}-\langle\hat{A}\rangle)\psi(t,\bm{x})$
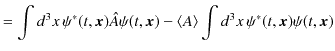	$\displaystyle =\int d^{3}x\,\psi^{}(t,\bm{x})\hat{A}\psi(t,\bm{x})-\langle A\rangle\int d^{3}x\,\psi^{}(t,\bm{x})\psi(t,\bm{x})$
	$\displaystyle =\langle\hat{A}\rangle-\langle\hat{A}\rangle\cdot1$
	$\displaystyle =0$

となってしまいます．バラツキのある理想測定値を平均すると期待値になるので，この演算子 $\hat{\Delta A}$ の期待値が 0 になるのは理解できます．しかし，このままでは，理想測定値のバラツキの程度を表すことができません．そこで，演算子 $\hat{\Delta A}$ を2乗して期待値をとることにします．

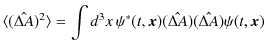
$\displaystyle \langle(\hat{\Delta A})^{2}\rangle=\int d^{3}x\,\psi^{*}(t,\bm{x})(\hat{\Delta A})(\hat{\Delta A})\psi(t,\bm{x})$

この量を分散といいます．ここで，一般にエルミート演算子は，

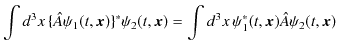
$\displaystyle \int d^{3}x\,\{\hat{A}\psi_{1}(t,\bm{x})\}^{*}\psi_{2}(t,\bm{x})=\int d^{3}x\,\psi_{1}^{*}(t,\bm{x})\hat{A}\psi_{2}(t,\bm{x})$

という関係で表せますので，以下計算すると，

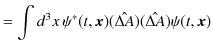$\displaystyle \langle(\hat{\Delta A})^{2}\rangle$	$\displaystyle =\int d^{3}x\,\psi^{*}(t,\bm{x})(\hat{\Delta A})(\hat{\Delta A})\psi(t,\bm{x})$
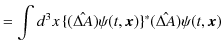	$\displaystyle =\int d^{3}x\,\{(\hat{\Delta A})\psi(t,\bm{x})\}^{*}(\hat{\Delta A})\psi(t,\bm{x})$
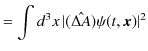	$\displaystyle =\int d^{3}x\,\vert(\hat{\Delta A})\psi(t,\bm{x})\vert^{2}$
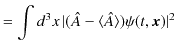	$\displaystyle =\int d^{3}x\,\vert(\hat{A}-\langle\hat{A}\rangle)\psi(t,\bm{x})\vert^{2}$

となります．いま，波動力学的理想装置で，複数回の理想実験を実行して，複数のバラツキのある理想測定値を得ている場合を考えています．ここで，その中の確定した1つの理想測定値に着目します．この1つの理想測定値を測定するとき，波動関数の量子飛躍が起こっているはずです．

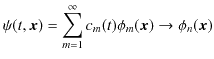
$\displaystyle \psi(t,\bm{x})=\sum_{m=1}^{\infty}c_{m}(t)\phi_{m}(\bm{x})\to\phi_{n}(\bm{x})$

添え字のは，複数ある，時間に依存しない波動関数を区別するためのものです．その中のある番目の波動関数の状態に量子飛躍するとしています．（"量子状態（波動関数と確率振幅）" のChapterの内容を思い出して下さい．）この際，期待値も量子飛躍した時間に依存しない波動関数 $\phi(\bm{x})$ で計算された，次の量に置き換えることにします．

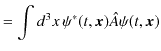$\displaystyle \langle\hat{A}\rangle$	$\displaystyle =\int d^{3}x\,\psi^{*}(t,\bm{x})\hat{A}\psi(t,\bm{x})$
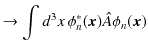	$\displaystyle \to\int d^{3}x\,\phi_{n}^{*}(\bm{x})\hat{A}\phi_{n}(\bm{x})$

この量は，もはや期待値とは言えませんが，バラツキのある理想測定値のうちの1つの確定値と考えることができます．（この確定値を $a_{n}$ と置きます．）このとき，分散は 0 です．すなわち，

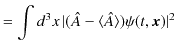$\displaystyle \langle(\hat{\Delta A})^{2}\rangle$	$\displaystyle =\int d^{3}x\,\vert(\hat{A}-\langle\hat{A}\rangle)\psi(t,\bm{x})\vert^{2}$
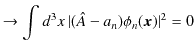	$\displaystyle \to\int d^{3}x\,\vert(\hat{A}-a_{n})\phi_{n}(\bm{x})\vert^{2}=0$

となります．この式の矢印の右にある積分の被積分関数は絶対値の2乗の量であるので，常に正または 0 です．したがって，この積分が 0 になるということは，

	$\displaystyle (\hat{A}-a_{n})\phi_{n}(\bm{x})=0$
$% latex2html id marker 2863 $\displaystyle \therefore$$	$\displaystyle \hat{A}\phi_{n}(\bm{x})=a_{n}\phi_{n}(\bm{x})$

が成立していることになります．

　最後の方程式を固有値方程式， $\phi_{n}(\bm{x})$ を固有関数， $a_{n}$ を固有値といいます．固有値方程式においては，演算子 $\hat{A}$ が関数 $\phi(\bm{x})$ に作用し，その結果が $\phi(\bm{x})$ の定数倍になる関係になっています．そして，固有値方程式を解く問題を固有値問題といいます．固有値は跳び跳びの値をもつ離散固有値の場合と，連続的な値をもつ連続固有値の場合がありますが，どちらも一般に，解は無限個あります．これまでの議論により，波動力学的理想装置における理想測定値は，この固有値の中のいずれかになることは確実であることが理解できます．特に，波動関数 $\phi_{n}(\bm{x})$ の状態で測定すると，確実に測定値 $a_{n}$ になります．しかし，時間に依存する波動関数 $\psi(t,\bm{x})$ の状態で測定する場合，測定する前に固有値の中の特定のどれになるかを決定することは不可能であり，その中の確率のみを求めることができます．（確率の求め方は "波動力学の展開" のChapterを参照して下さい．）固有値問題の例としては，時間に依存しないシュレディンガー方程式，

$\displaystyle \hat{H}(\bm{x},-i\hbar\bm{\nabla})\phi(\bm{x})=E\phi(\bm{x})$

を挙げることができます．この微分方程式を解くと，波動関数は固有関数として，エネルギーはエネルギー固有値として求められます．具体的な固有値問題の解法については，例を取り扱っている後の4つのChapterを見て下さい．また，固有値問題の詳しい議論は "波動力学の展開" のChapterを参照して下さい．

　固有値について，1つ定理を挙げておきます．それは，

定理8.1 "エルミート演算子の固有値は実数になります．"

というものです．この定理を証明しておきます．固有値方程式，

$\displaystyle \hat{A}\phi_{n}(\bm{x})=a_{n}\phi_{n}(\bm{x})$

が成立するものとします．ここで， $\hat{A}$ がエルミート演算子の場合，

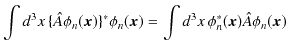	$\displaystyle \int d^{3}x\,\{\hat{A}\phi_{n}(\bm{x})\}^{}\phi_{n}(\bm{x})=\int d^{3}x\,\phi_{n}^{}(\bm{x})\hat{A}\phi_{n}(\bm{x})$
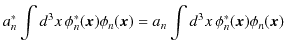$% latex2html id marker 2893 $\displaystyle \therefore$$	$\displaystyle a_{n}^{}\int d^{3}x\,\phi_{n}^{}(\bm{x})\phi_{n}(\bm{x})=a_{n}\int d^{3}x\,\phi_{n}^{*}(\bm{x})\phi_{n}(\bm{x})$
$% latex2html id marker 2895 $\displaystyle \therefore$$	$\displaystyle a_{n}^{*}=a_{n}$

となります．したがって，固有値 $a_{n}$ は実数です．（証明終．）理想実験による測定値は固有値のいずれかになりますが，その固有値が実数であることが保証されたことになります．

　量子力学における物理量一般のことをオブザーバブルといいます．その意味は観測可能量です．ここで，物理量についての概念の発展の繋がりをまとめておきます．

　"古典的物理量
　→波動力学的物理量
　　　数学的表現（線形エルミート演算子）
　　　理想測定値の平均値（期待値）
　　　理想測定値の個別値（固有値）
　→量子力学的物理量（オブザーバブル）"