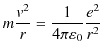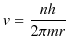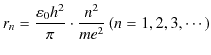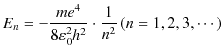J Simplicity 原子構造と前期量子論

Chapter4 原子構造と前期量子論

4.1 原子モデルと原子によるα粒子の散乱実験

光と物質の2重性が明らかになっていくのと並行して，原子内部の構造についての研究も進められました．当時，原子構造のモデルは，まず，1904年にJ.J.トムソンによって考案されました．（原子的性質のChapterでのトムソンの実験をした物理学者と同一人物です．）それは原子の内部はレーズンパンのようなものであるというモデルです．大きさが $10^{-10}[m]$ 程度の正に帯電した球形の連続的な生地の中に，電子がレーズンのように散らばっていて，全体として電気的に中性になっているという内容になっていました．

　原子の構造を探るため，1909年，ラザフォードの指導のもとに，ガイガーとマルスデンは，原子にα粒子を衝突させ散乱させる実験を行いました．実験の内容は，ラジウムから出るα粒子を薄い金属箔に衝突させるというものです．実験結果を2項目にまとめておきます．

入射したα粒子の大部分はそのまま直進して散乱されません．
ごく少数のα粒子だけ，90°を越え，180°近くの大きな散乱角をもっています．

トムソンのモデルでは，2番目の特徴を説明することができません．ラザフォードは，原子の中心に正に帯電した原子核というものを考え，その周りに電子が回っているというモデルを提唱しました．このモデルによって，ラザフォードは量子論以前の古典論により理論を展開し，実験結果の2つの特徴を見事に説明しました．（1911年．）

4.2 水素原子のスペクトル

水素の気体をいれた放電管からでる光を，プリズムのような分光器にかけると，波長の違いによってできる跳び跳びの輝線である線スペクトルがみられます．1890年，線スペクトルの波長λを表す一般式は，リュードベリによって発見されました．その式は，

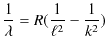
$\displaystyle \dfrac{1}{\lambda}=R(\dfrac{1}{\ell^{2}}-\dfrac{1}{k^{2}})$

と表されます．これをリュードベリの公式といいます．ここで，はリュードベリ定数といい，

$\displaystyle R=1.097\times10^{7}[1/m]$

であることが測定されました．また， $\ell$ とは自然数で，

	$\displaystyle \ell=1,2,3,\cdots$
	$\displaystyle k=\ell+1,\ell+2,\ell+3,\cdots$

の関係を満たす線スペクトルが，観測されました．（ $\ell$ との意味は実験結果を忠実に再現するという事実以上のことは，理解されていませんでした．次のSectionのボーアの理論で初めて理解されるのです．）リュードベリの公式は実験結果を再現する式ですが，経験式であって，当時あった法則から導出されたものではありませんでした．その後，水素原子の構造を研究し，リュードベリの公式を導出したのがボーアです．スペクトルには，水素原子の構造に関する暗号のような情報が含まれていたのです．

4.3 ボーアの前期量子論

前述したように，1911年，ラザフォードは原子核の存在を実験によって明らかにしました．それに注目したボーアは，1913年に最も簡単な構造をもつ原子である水素原子の構造として，1個の原子核の周りの円軌道を，軽い1個の電子が回り続けるという原子構造のモデルを考えて理論を展開しました．この理論は前Sectionのリュードベリの公式を導き，その意味を明らかにするものとなりました．

　電磁気学によれば，電子のような電荷をもった粒子が円運動をすると，その回転数に等しい振動数の電磁波が放出され，電子はエネルギーを失って原子核に落ち込んでしまうことになります．この困難を克服すべく，ボーアは次の量子条件と呼ばれる仮定をしました．

　"電子の運動量の大きさと円周の長さとの積が，プランク定数hの定数倍に等しいときだけ，電子は安定な状態になります．"

この条件を式で表現すると，

$\displaystyle mv\times2\pi r=nh\,(n=1,2,3,\cdots)$

(4.1)

となります．ここで，は電子の質量，は電子の運動の速さ，は軌道半径です．あるいは，を電子の運動量の大きさ，を座標変数として，

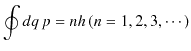
$\displaystyle \oint dq\,p=nh\,(n=1,2,3,\cdots)$

とすることもできます．ただし，積分は電子の軌道に沿って1周するものとします．量子条件を満たす特別な状態を定常状態といい，定常状態における電子のエネルギーをエネルギー順位といいます．ここで，量子条件の物理的意味について考えておきましょう．(4.1)式は，次のように変形されます．

$\displaystyle 2\pi r$	$\displaystyle =n\dfrac{h}{mv}$
	$\displaystyle =n\dfrac{h}{p}$

ここで，アインシュタイン-ド・ブロイの関係式，

$\displaystyle p=\dfrac{h}{\lambda}$

より，

$\displaystyle 2\pi r=n\lambda$

となります．ただし， $\lambda$ はド・ブロイ波の波長を表します．この式は，

$\displaystyle ($ 円周の長さ $\displaystyle )=($ 整数 $\displaystyle )\times($ ド・ブロイ波の波長 $\displaystyle )$

となっています．すなわち，ド・ブロイ波が電子の軌道上で，定常波を形成する条件を表しています．実はボーアの理論が考えられた当時，まだド・ブロイの物質波の理論は存在しませんでした．量子条件の意味は，後になってから理解されたのです．例として，のときの定常波の様子を示しておきます．

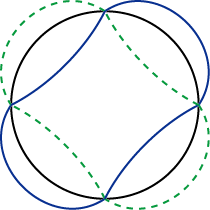
量子条件（n=2）

Figure4.1: 量子条件（n=2）

　電子は原子核の周りを等速円運動しています．（このとき，電子を粒子と考えていますが，状況に応じて電子を波動と考えたり，粒子と考えたりすることは，電子の2重性によるものです．）電子の軌道の半径を，速さを，電気素量をとすると，円の中心方向への運動方程式は，

$\displaystyle m\dfrac{v^{2}}{r}=\dfrac{1}{4\pi\varepsilon_{0}}\dfrac{e^{2}}{r^{2}}$

(4.2)

となります．円の中心方向にはクーロン力が働いていて，これが向心力の役目をしています．ここで，量子条件(4.1)式より，

$\displaystyle v=\dfrac{nh}{2\pi mr}$

(4.3)

となります．(4.3)式を(4.2)式に代入して計算します．

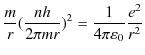	$\displaystyle \dfrac{m}{r}(\dfrac{nh}{2\pi mr})^{2}=\dfrac{1}{4\pi\varepsilon_{0}}\dfrac{e^{2}}{r^{2}}$
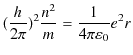$% latex2html id marker 672 $\displaystyle \therefore$$	$\displaystyle (\dfrac{h}{2\pi})^{2}\dfrac{n^{2}}{m}=\dfrac{1}{4\pi\varepsilon_{0}}e^{2}r$

故に，

$\displaystyle r_{n}=\dfrac{\varepsilon_{0}h^{2}}{\pi}\cdot\dfrac{n^{2}}{me^{2}}\,(n=1,2,3,\cdots)$

(4.4)

となります．(4.4)式より，電子の軌道半径が跳び跳びの値をとり，自然数が軌道の番号であることがわかります．すなわち， $r_{n}$ は内側から番目の軌道の半径を示します．

　次に定常状態のエネルギーを求めましょう．は電子の運動エネルギーとクーロン力によるポテンシャルの和であるので，

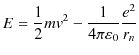
$\displaystyle E=\dfrac{1}{2}mv^{2}-\dfrac{1}{4\pi\varepsilon_{0}}\dfrac{e^{2}}{r_{n}}$

ですが，(4.2)式より，

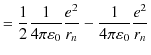$\displaystyle E$	$\displaystyle =\dfrac{1}{2}\dfrac{1}{4\pi\varepsilon_{0}}\dfrac{e^{2}}{r_{n}}-\dfrac{1}{4\pi\varepsilon_{0}}\dfrac{e^{2}}{r_{n}}$
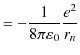	$\displaystyle =-\dfrac{1}{8\pi\varepsilon_{0}}\dfrac{e^{2}}{r_{n}}$

と計算されます．この式に(4.4)式を代入して計算すると，

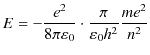
$\displaystyle E=-\dfrac{e^{2}}{8\pi\varepsilon_{0}}\cdot\dfrac{\pi}{\varepsilon_{0}h^{2}}\dfrac{me^{2}}{n^{2}}$

となり，故に，

$\displaystyle E_{n}=-\dfrac{me^{4}}{8\varepsilon_{0}^{2}h^{2}}\cdot\dfrac{1}{n^{2}}\,(n=1,2,3,\cdots)$

(4.5)

となります． $E_{n}$ は内側から番目の軌道のエネルギーを意味し，エネルギー準位といいます．軌道が外側になるほどエネルギーは高くなることに注意して下さい．ここで，ボーアは次の第2の条件を置きました．すなわち，振動数条件として，

　" から $n=\ell$ の定常状態に移るとき，エネルギーの差 $E_{k}-E_{\ell}$ と同じエネルギーの光子が1個放出されます．"

と仮定しました．外側から内側に電子が落ち込んだ時，余ったエネルギーが光子のエネルギーに変化すると考えたのです．

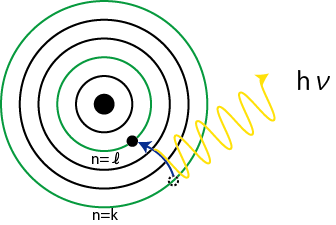
振動数条件

Figure4.2: 振動数条件

振動数条件を式で表せば，

$\displaystyle h\nu=E_{k}-E_{\ell}$

となります．この式に(4.5)式を代入して計算します．

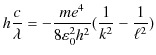	$\displaystyle h\dfrac{c}{\lambda}=-\dfrac{me^{4}}{8\varepsilon_{0}^{2}h^{2}}(\dfrac{1}{k^{2}}-\dfrac{1}{\ell^{2}})$
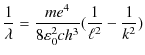$% latex2html id marker 712 $\displaystyle \therefore$$	$\displaystyle \dfrac{1}{\lambda}=\dfrac{me^{4}}{8\varepsilon_{0}^{2}ch^{3}}(\dfrac{1}{\ell^{2}} -\dfrac{1}{k^{2}})$

最後の式はリュードベリの公式を再現したものになっています．確かに右辺の分数になっている係数を計算すると，

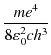$\displaystyle \dfrac{me^{4}}{8\varepsilon_{0}^{2}ch^{3}}$	$\displaystyle =\dfrac{9.109\times10^{-31}[kg]\times(1.602\times10^{-19}[C])^{4}... ...}[F/m])^{2}\times2.998\times10^{8}[m/s]\times(6.626\times10^{-34}[J\cdot s])^3}$
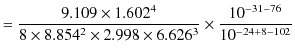	$\displaystyle =\dfrac{9.109\times1.602^{4}}{8\times8.854^{2}\times2.998\times6.626^{3}}\times\dfrac{10^{-31-76}}{10^{-24+8-102}}$
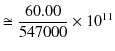	$\displaystyle \cong\dfrac{60.00}{547000}\times10^{11}$
	$\displaystyle =0.00010968\cdots\times10^{11}$
	$\displaystyle \cong1.097\times10^{7}[1/m]$

となり，完全にリュードベリ定数と一致します．また，自然数 $\ell$ やは，電子の軌道の内側から数えて何番目かを表すという意味があることも理解されました．

　1913年にボーアは，このようにリュードベリの公式を導くことに成功し，一段と高いレベルの理論を形成することができました．しかし，量子条件と振動数条件という天下りの仮定をしている点，2重性の本質について踏み込んだ議論をしていない点で不満が残ります．その後，1920年代半ばに量子力学という真の理論が誕生しました．水素原子の構造についても，量子力学の基礎方程式であるシュレディンガー方程式から解明することができるのです．このことについては，"束縛状態（例: 中心力場内の粒子）" のChapterで明らかにしましょう．量子力学が完成した後，ボーアの理論は前期量子論として，過渡的な理論としての意義をもつようになったのです．