Part2 波動力学の成立
Chapter5 不確定性原理
5.1 量子力学について
このChapterから完成された量子力学について考えていくことにします.光と物質の2重性の問題や前期量子論の不完全性を乗り越えて創造された,真の理論としての量子力学の概念と原理,さらに理論体系を導入していくことにします.
量子力学の理論について,大まかな流れを触れておくことにします.ド・ブロイの物質波の着想のもとに,1926年,シュレディンガーが創った理論体系を波動力学といいます.一方,その1年前の1925年,ハイゼンベルクは別の体系である行列力学を創始していました.その当時,この2つの物理体系は,計算方法は異なりますが,いつも同じ結果を出すことがわかってきました.そこで,シュレディンガーは2つの理論を分析し,両者の同等性を証明しました.さらにディラックは,この2つの理論を特殊な場合として取り込んでいる完全に一般的な体系を構築しました.これを変換理論といいます.(1927年)ここに,完成した量子力学が誕生したのです.その後,時代は下がりますが,ファインマンは斬新な着想のもとに,新しい量子力学を創り上げました.これを経路積分といいます.(1948年)これから,Part2では,波動力学について詳しく取り扱うことにします.というのも,波動力学の理論が最も理解し易いからです.残りの3つの理論についてはPart3で見ていくことにします.
ここで,物理学の分類に関する言葉の定義を確認しておきましょう.ニュートン力学やマクスウェル電磁気学等,量子力学以前の理論を古典論といいます.相対性理論は20世紀になってから創始された理論であり,現代物理学に属しますが,量子力学による理論以前の物理学ですので,古典論の範疇に属します.(古典物理学と古典論の違いに注意して下さい.)特に,量子力学以降の物理理論は量子論と総称することにします.(量子論という言葉と古典論という言葉は対立する関係にあります.)場の量子論や弦理論は量子論になります.
5.2 不確定性原理
ニュートン力学においては,野球のボールや天体等,その運動において座標と運動量を厳密に,しかも同時に決定することができました.この事実はミクロな世界においては,そのまま成立するのでしょうか?
この問題について,2重性をもつ電子のような1個の量子の波動で取り扱うことにしましょう.簡単のため,1次元の場合に設定し,波動が図のように波束をつくっている場合を考えます.
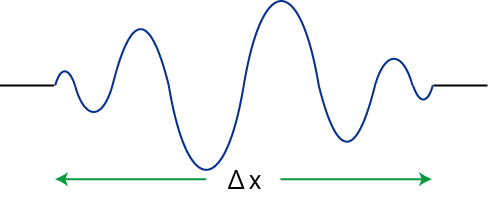
Figure5.1: 不確定性原理
波束の広がりである ![]() が,無限大になれば正弦波の場合であり,
が,無限大になれば正弦波の場合であり,![]() が微小のときは波束が局在していることになります.図の波束は,これら2つの場合を極限として含んでいることになります.量子の波動の正体が何であるかについては,まだ考えていませんが,この
が微小のときは波束が局在していることになります.図の波束は,これら2つの場合を極限として含んでいることになります.量子の波動の正体が何であるかについては,まだ考えていませんが,この ![]() の中に量子が存在しているはずです.したがって,量子の座標には
の中に量子が存在しているはずです.したがって,量子の座標には ![]() の幅があることになります.波数
の幅があることになります.波数 ![]() は長さ
は長さ ![]() の中に含まれる波の数でありましたので,
の中に含まれる波の数でありましたので,![]() の領域にある波の数は,
の領域にある波の数は,
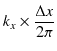
で与えられます.ここで,![]() の領域にある波束の両端の振幅が小さくなっていて,波の数を厳密に数えることができないことに注意しましょう.このとき,波数
の領域にある波束の両端の振幅が小さくなっていて,波の数を厳密に数えることができないことに注意しましょう.このとき,波数 ![]() の不確定さを
の不確定さを
![]() とし,
とし,![]() の領域での波の数に,大雑把に見積もって,1個程度の不確定性があるとします.この場合,
の領域での波の数に,大雑把に見積もって,1個程度の不確定性があるとします.この場合,
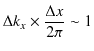
の関係が成立します.(![]() は大体の程度が一致することを示します.)故に,
は大体の程度が一致することを示します.)故に,
となります.さらに,両辺に ![]() をかけて,量子についての関係である,アインシュタイン-ド・ブロイの関係式を使うと,
をかけて,量子についての関係である,アインシュタイン-ド・ブロイの関係式を使うと,
が導かれます.ここで,
![]() は運動量の不確定さを表し,
は運動量の不確定さを表し,![]() はプランク定数です.また,
はプランク定数です.また,
![]() でしたね.最後の関係をハイゼンベルクの不確定性原理といいます.
でしたね.最後の関係をハイゼンベルクの不確定性原理といいます.
不確定性原理は,ミクロ世界において,座標と運動量を同時に決定することが不可能であることを意味しています.仮に,量子の座標を完全に正確に決定すると,
![]() になります.これは,1点に局在した波束に対応しますが,このとき不確定性原理より,
になります.これは,1点に局在した波束に対応しますが,このとき不確定性原理より,
![]() になり,運動量の値が全くわからなくなります.逆に,運動量を完全に正確に決定すると,
になり,運動量の値が全くわからなくなります.逆に,運動量を完全に正確に決定すると,
![]() になります.この場合は不確定性原理より,
になります.この場合は不確定性原理より,
![]() になり,座標がわからなくなります.波束が無限大に広がっているときとは,例えば,無限に広がっている正弦波等が対応します.不確定性原理は,量子力学においては,もはや常識が通用せず,古典論と決別しなければならないことを示しているのです.
になり,座標がわからなくなります.波束が無限大に広がっているときとは,例えば,無限に広がっている正弦波等が対応します.不確定性原理は,量子力学においては,もはや常識が通用せず,古典論と決別しなければならないことを示しているのです.
以上の1次元の議論を3次元に拡張します.この場合の不確定性原理は,![]() 方向,
方向,![]() 方向,
方向,![]() 方向をとり,次のように表すことができます.
方向をとり,次のように表すことができます.