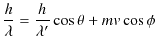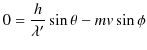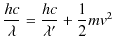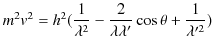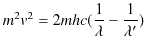J Simplicity 光と物質の2重性

Chapter3 光と物質の2重性

3.1 光の2重性

光とは何でしょうか？この問題については，古くから論争が続いていました．力学を創ったニュートンは，光は粒子であるとし，様々な現象を説明しました．それに対して，ホイヘンスは光の波動説を唱え，ニュートンの粒子説と対立しました．その後，19世紀の初めにヤングにより，2重スリットの実験が行われ，光が干渉することが判明しました．干渉は波動でしか起こらない現象であり，波動説が有利な立場になりました．さらに，マクスウェル電磁気学が確立して，光は電磁波の一種であることが理解され，光が波動であることは疑いのないものとされました．

　光の波動説が定説となり，しばらくした後，19世紀の終わりに光電効果という現象が発見されました．これは紫外線や青色の光など，振動数の大きい電磁波を金属の表面に当てると，電子が跳び出す現象です．実験を繰り返し，次のような特徴を見出すことができました．

当てる電磁波の振動数が大きい程，跳び出す電子の運動エネルギーは大きくなります．反対に電磁波の振動数が小さくなると，跳び出す電子の運動エネルギーが小さくなり，やがて電子は跳び出さなくなります．振動数が小さいと，電磁波の振幅を大きくしても電子は跳び出しません．
当てる電磁波の振幅を増加させても，跳び出す電子の運動エネルギーには影響を与えません．ただし，跳び出す電子の個数が増えます．

これらの特徴について，光が波動であると考えると全く説明がつきません．つまり，当てる電磁波の振動数によって跳び出す電子の運動エネルギーが変わるなら，電子を跳び出させた電磁波のもつエネルギーが変化したことになります．しかし，波動のエネルギーは，振動数だけでなく振幅にも関係してきます．振幅の大きな波動程，大きなエネルギーをもつという特徴があるので，振幅を大きくすると，跳び出す電子の運動エネルギーは大きくなるはずです．（特徴の2と矛盾しています．）特に，光の振動数を小さくしても振幅を大きくしてやれば，電子は跳び出してくるはずです．（特徴の1と矛盾しています．）このような状況の中で，1905年，アインシュタインはプランクのエネルギー量子仮説に基づき，光量子仮説を発表しました．（ちなみに，1905年，特許局の事務員だったアインシュタインは特殊相対性理論，ブラウン運動の理論も発表しています．この年は奇跡の年と呼ばれています．）この理論の中で，アインシュタインは振動数が $\nu$ の電磁波は $h\nu$ のエネルギーをもった粒子の集まりであると仮定し，その粒子を光量子（光子ともいいます．）と呼びました．特に，光量子のエネルギーは振動数のみに依存し，振幅とは無関係であるとしました．この仮説により，光電効果は次のように説明されます．振動数の大きな電磁波は，エネルギー $h\nu$ が大きな光量子の集団になります．そのエネルギーの大きな光量子を金属の表面にぶつけると，金属と電子の結合が切れて電子が跳び出してくるのです．振動数 $\nu$ が大きい程，光量子のエネルギー $h\nu$ が大きいので，電子は勢いよく跳び出すことになります．逆に，ある一定の振動数以下になると，金属と電子の結合を切るだけのエネルギー（これを仕事関数と言います．）を光量子がもてないため，電子は跳び出せなくなります．跳び出した電子1個の運動エネルギーの最大値 $\frac{1}{2}mv^{2}$ は，光量子1個のエネルギー $h\nu$ と次の関係にあります．

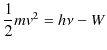
$\displaystyle \dfrac{1}{2}mv^{2}=h\nu-W$

つまり，光量子1個で1個の電子を叩き出しますが，光量子1個のエネルギーのうち一部を，電子を剥ぎ取るために仕事関数として使い，残りのエネルギーを電子の運動エネルギーに使うということになります．また，電磁波の振幅が大きくなるということは，電磁波の強度が増すことに相当します．このとき光量子の個数が増えると考えることができます．当てる電磁波の振幅が大きくなっても，光量子1つ1つのエネルギーは変化しませんが，光量子の個数が増えるので，それだけ跳び出す電子の個数が増加することになります．このようにアインシュタインは光量子仮説によって光電効果を完全に説明して，光の粒子説を復活させました．

　アインシュタインが光子のエネルギーを，プランクのエネルギー量子仮説により，

$\displaystyle E=h\nu$

としたことは，上で述べた通りです．ここで，粒子である光子の運動量の大きさを表す式を導いてみましょう．特殊相対性理論より，

$\displaystyle E^{2}=c^{2}p^{2}+m^{2}c^{4}$

という関係式が成立しました．光子の場合，質量であるので，その運動量の大きさは，次のように表されます．

$\displaystyle p$	$\displaystyle =\dfrac{E}{c}$
	$\displaystyle =\dfrac{h\nu}{\nu\lambda}$

よって，

$\displaystyle p=\dfrac{h}{\lambda}$

が成立します．光子について，エネルギーと運動量の大きさに関するこれら2つの関係式をアインシュタインの関係式といいます．

　光と同じ電磁波の一種であるX線は，ブラッグの実験というものにより，波動性をもつことが確認されていました．1923年，コンプトンはコンプトン効果と呼ばれる実験により，X線が粒子性を併せ持つことを確認しました．それでは，コンプトン効果について見ていくことにしましょう．この実験はX線をターゲットとなる物質に入射すると，X線が散乱されるという簡単なものです．次の2つの特徴があります．

散乱されたX線の中には，入射したX線の波長よりも長い波長のものが混ざります．
散乱角が大きくなる程，散乱されたX線の波長が長くなります．

この特徴を，X線がアインシュタインの関係式を満たす粒子であると考えて，以下のように説明してみましょう．

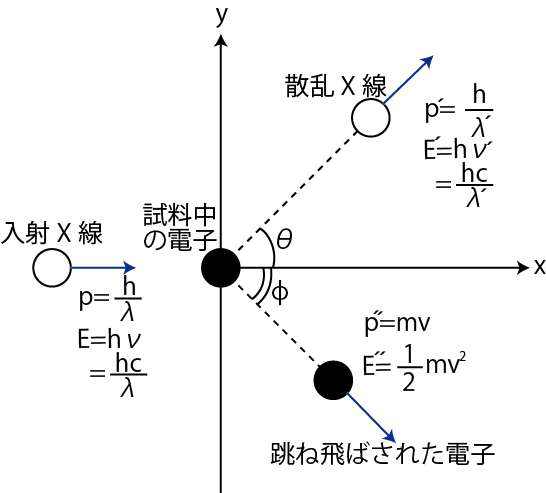
コンプトン効果

Figure3.1: コンプトン効果

この実験は，図のように，入射X線の光子と試料中の電子との2次元の完全弾性散乱です．このとき，方向と方向についての運動量保存則より，

	$\displaystyle \dfrac{h}{\lambda}=\dfrac{h}{\lambda'}\cos\theta+mv\cos\phi$	(3.1)
	$\displaystyle 0=\dfrac{h}{\lambda'}\sin\theta-mv\sin\phi$	(3.2)

が成立します．また，エネルギー保存則より，

$\displaystyle \dfrac{hc}{\lambda}=\dfrac{hc}{\lambda'}+\dfrac{1}{2}mv^{2}$

(3.3)

が成り立ちます．以上の3つの式を連立して解いてみます．(3.1)式より，

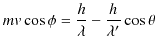	$\displaystyle mv\cos\phi=\dfrac{h}{\lambda}-\dfrac{h}{\lambda'}\cos\theta$
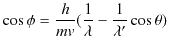$% latex2html id marker 601 $\displaystyle \therefore$$	$\displaystyle \cos\phi=\dfrac{h}{mv}(\dfrac{1}{\lambda}-\dfrac{1}{\lambda'}\cos⁡\theta)$

となります．(3.2)式より，

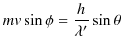	$\displaystyle mv\sin\phi=\dfrac{h}{\lambda'}\sin⁡\theta$
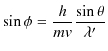$% latex2html id marker 604 $\displaystyle \therefore$$	$\displaystyle \sin\phi=\dfrac{h}{mv}\dfrac{\sin\theta⁡}{\lambda'}$

となります．ここで，公式，

$\displaystyle \cos^{2}\phi+\sin^{2}\phi=1$

を使い，以下のように計算します．

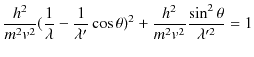	$\displaystyle \dfrac{h^{2}}{m^{2}v^{2}}(\dfrac{1}{\lambda}-\dfrac{1}{\lambda'}\cos\theta)^{2}+\dfrac{h^{2}}{m^{2}v^{2}}\dfrac{\sin^{2}\theta}{\lambda'^{2}}=1$
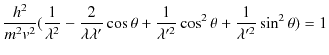$% latex2html id marker 609 $\displaystyle \therefore$$	$\displaystyle \dfrac{h^{2}}{m^{2}v^{2}}(\dfrac{1}{\lambda^{2}}-\dfrac{2}{\lambd... ...+\dfrac{1}{\lambda'^{2}}\cos^{2}\theta+\dfrac{1}{\lambda'^{2}}\sin^{2}\theta)=1$
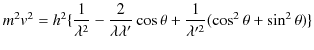$% latex2html id marker 611 $\displaystyle \therefore$$	$\displaystyle m^{2}v^{2}=h^{2}\{\dfrac{1}{\lambda^{2}}-\dfrac{2}{\lambda\lambda'}\cos\theta+\dfrac{1}{\lambda'^{2}}(\cos^{2}\theta+\sin^{2}\theta)\}$

故に，

$\displaystyle m^{2}v^{2}=h^{2}(\dfrac{1}{\lambda^{2}}-\dfrac{2}{\lambda\lambda'}\cos\theta+\dfrac{1}{\lambda'^{2}})$

(3.4)

となります．ここで，(3.3)式より，

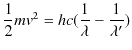
$\displaystyle \dfrac{1}{2}mv^{2}=hc(\dfrac{1}{\lambda}-\dfrac{1}{\lambda'})$

よって，

$\displaystyle m^{2}v^{2}=2mhc(\dfrac{1}{\lambda}-\dfrac{1}{\lambda'})$

(3.5)

となります．(3.4)式と(3.5)式より，

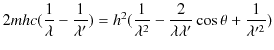
$\displaystyle 2mhc(\dfrac{1}{\lambda}-\dfrac{1}{\lambda'})=h^{2}(\dfrac{1}{\lambda^{2}}-\dfrac{2}{\lambda\lambda'}\cos\theta+\dfrac{1}{\lambda'^{2}})$

となります．この式の両辺に，

$\displaystyle \dfrac{\lambda\lambda'}{h}$

をかけて，計算します．

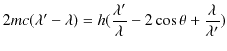	$\displaystyle 2mc(\lambda'-\lambda)=h(\dfrac{\lambda'}{\lambda}-2\cos\theta+\dfrac{\lambda}{\lambda'})$
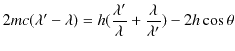$% latex2html id marker 624 $\displaystyle \therefore$$	$\displaystyle 2mc(\lambda'-\lambda)=h(\dfrac{\lambda'}{\lambda}+\dfrac{\lambda}{\lambda'})-2h\cos\theta$

ここで， $\lambda'\cong\lambda$ のとき，

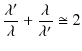
$\displaystyle \dfrac{\lambda'}{\lambda}+\dfrac{\lambda}{\lambda'}\cong2$

が成立するので，

	$\displaystyle 2mc(\lambda'-\lambda)\cong2h-2h\cos\theta$
$% latex2html id marker 631 $\displaystyle \therefore$$	$\displaystyle 2mc(\lambda'-\lambda)\cong2h(1-\cos\theta)$
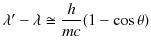$% latex2html id marker 633 $\displaystyle \therefore$$	$\displaystyle \lambda'-\lambda\cong\dfrac{h}{mc}(1-\cos\theta)$
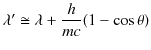$% latex2html id marker 635 $\displaystyle \therefore$$	$\displaystyle \lambda'\cong\lambda+\dfrac{h}{mc}(1-\cos\theta)$

となります．最後の式は，コンプトン効果の2つの特徴をよく表しています．つまり，X線の粒子性が確認されたのです．以上のように，光（電磁波）は粒子としての性質をもつことが確認されました．しかし，従来の波動としての様々な現象が存在することも事実です．光（電磁波）は波動として振る舞うときと，粒子として振る舞うときがあるらしいことが判明してきたのです．このような波動性と粒子性の2つの性質を併せ持つことを，光（電磁波）の2重性と呼ぶことにします．光（電磁波）の2重性はミクロ世界の著しい特徴になっています．

3.2 物質の2重性

光（電磁波）の2重性が明らかになってきた頃，1924年，ド・ブロイは，光に2重性があるのならば，粒子であるはずの電子にも波動性があるのではないかと考えました．電子が粒子であることは疑いのないものとされていましたが，その電子に波動性があるのではないかと思い付いたのは，2重性こそがミクロ世界の本質であることを，ド・ブロイが見抜いたのではないかと推測されます．その後，電子線回折の実験等，電子の波動性を確認する実験が行われました．物質（電子，陽子，中性子等）は粒子性と波動性の2重性を併せ持つことが理解されるようになったのです．物質（電子，陽子，中性子等）の波動のことをド・ブロイ波，または物質波といいます．

　光子の場合，エネルギーと運動量の大きさは，次の2つの式のように与えられることが，アインシュタインによって理解されましたね．

	$\displaystyle E=h\nu$
	$\displaystyle p=\dfrac{h}{\lambda}$

ド・ブロイはこれらの関係式が電子の場合もそのまま成立すると考えました．この2つの式は，物質（電子，陽子，中性子等）については，ド・ブロイの関係式といいます．

3.3 量子と2重性の本質

光（電磁波）と物質（電子，陽子，中性子等）は2重性を併せ持つことが，明らかになってきました．ここで，ミクロ世界において，2重性をもつものを量子と名付けることにしましょう．光子，電子，陽子，中性子等は量子になります．また，素粒子論でのクォークやレプトンも量子であるといえます．いままでの議論から，量子については次の2つの式からなるアインシュタイン-ド・ブロイの関係式が成立することが理解されます．

	$\displaystyle E=h\nu$
	$\displaystyle p=\dfrac{h}{\lambda}$

これら2つの式を変形しておきましょう．

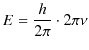	$\displaystyle E=\dfrac{h}{2\pi}\cdot2\pi\nu$
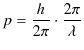	$\displaystyle p=\dfrac{h}{2\pi}\cdot\dfrac{2\pi}{\lambda}$

となりますが，ここで，

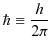
$\displaystyle \hbar\equiv\dfrac{h}{2\pi}$

とおくと，

	$\displaystyle E=\hbar\omega$
	$\displaystyle p=\hbar k$

となります．ただし， $\omega$ は角振動数，は波数です．これら2式もアインシュタイン-ド・ブロイの関係式といいます．これらの関係式の左辺はエネルギーや運動量の大きさといった，量子の粒子性に関係する量を含んでいます．一方，関係式の右辺は角振動数や波数といった，量子の波動性に関係する量を含んでいます．アインシュタイン-ド・ブロイの関係式は，量子の2重性を関係付ける式として理解されるのです．

　以上のように，20世紀の初め，光と物質の2重性が確認されましたが，最初はその本質が理解されませんでした．2重性はミクロ世界独特の特徴であって，常識的な従来の概念とは相いれないものであることが，その理由となっていました．1910年代から1920年代の初めにかけての過渡的な理論を前期量子論といいます．その理論の立場では，"物理学者は月・水・金の三日間は光が波動であると考え，火・木・土の三日間は光が粒子であると考えた" というように例えられました．（朝永振一郎著・量子力学1（みすず書房）P72から引用しました．電子も含め全ての量子についての2重性も同様に考えられたと思われます．）つまり，ある現象に対しては波動，別の現象に対しては粒子と考え分けて対応していたのです．しかし，このような理論が本物の理論であるとは到底考えられません．その後，1920年代半ばから1930年代にかけて満足のいく理論が確立しました．複数の物理学者達が創り上げた理論こそが，量子力学と呼ばれるものです．その理論の内容をPart2以降見ていくことにしましょう．その前に，次のChapterでは原子の構造，特にボーアの前期量子論について取り扱っておきましょう．