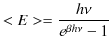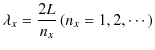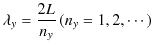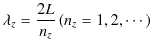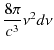Chapter2 エネルギー量子
2.1 黒体輻射の問題
19世紀の終わりごろ,黒体輻射の問題といわれるものがクローズアップされていました.絶対温度を上げると,物体は光,すなわち電磁波を放出します.このことを輻射といいます.特に,光(電磁波)を反射しない黒色の物体である黒体といわれるものでできている箱,すなわち空洞からの輻射を黒体輻射といいます.実験によると,空洞内の光(電磁波)のスペクトル(振動数と強度の関係)は絶対温度 ![]() のみに依存し,壁の物質,空洞の形,または大きさには一切関係しませんでした.実験から得られた黒体輻射のスペクトルを説明する式として,振動数の小さな領域でのレイリー-ジーンズの公式と,振動数の大きな領域でのウィーンの公式と呼ばれるものが経験式として判明していました.1900年,プランクは2つの公式を繋ぐ式として,次のプランクの公式を発見しました.
のみに依存し,壁の物質,空洞の形,または大きさには一切関係しませんでした.実験から得られた黒体輻射のスペクトルを説明する式として,振動数の小さな領域でのレイリー-ジーンズの公式と,振動数の大きな領域でのウィーンの公式と呼ばれるものが経験式として判明していました.1900年,プランクは2つの公式を繋ぐ式として,次のプランクの公式を発見しました.
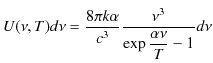
ここで,![]() は輻射の強度,
は輻射の強度,![]() はボルツマン定数,
はボルツマン定数,![]() は光速,
は光速,![]() は輻射の振動数です.また,
は輻射の振動数です.また,![]() は実験に合うように決定する定数になります.プランクの公式は全エネルギー領域に適用できて,レイリー-ジーンズの公式とウィーンの公式を極限として含むことが確かめられています.ここまでの話で終われば,プランクの公式の発見は単なる偶然に過ぎなかったかも知れません.この公式が成立する理由をプランクは徹底して追求しました.そのストーリーを次のSectionで見ていきましょう.
は実験に合うように決定する定数になります.プランクの公式は全エネルギー領域に適用できて,レイリー-ジーンズの公式とウィーンの公式を極限として含むことが確かめられています.ここまでの話で終われば,プランクの公式の発見は単なる偶然に過ぎなかったかも知れません.この公式が成立する理由をプランクは徹底して追求しました.そのストーリーを次のSectionで見ていきましょう.
2.2 エネルギー量子の発見
プランクの公式を理論的に導出することを,プランクは試みました.統計力学のボルツマン分布より,エネルギー ![]() の状態にある確率は,
の状態にある確率は,
![]() に比例することが分かっています.ここで,
に比例することが分かっています.ここで,
![]() です.当時の常識により,エネルギーは連続量であるとすると,その平均値は次のように計算されます.
です.当時の常識により,エネルギーは連続量であるとすると,その平均値は次のように計算されます.
 |
||
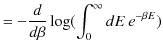 |
||
![$\displaystyle =-\dfrac{d}{d\beta}\log[-\dfrac{1}{\beta}e^{-\beta E}]_{0}^{\infty}$](ja_Chapter2_EnergyQuantum_images/img14.png) |
||
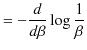 |
||
最後の式はエネルギー分配則であり,プランクの公式は導出されません.この間違った結論を導く議論の根本的な欠陥として,プランクはエネルギーが連続であるという,それまで当然のことと考えられていたことに問題があるのではないかと思い至りました.そして,エネルギーは跳び跳びの値をとる不連続量であるとするエネルギー量子仮説を思いついたのです.すなわち,エネルギーを,
と仮定してみたのです.(エネルギー素量としては,
で与えられます.これをエネルギー量子と呼ぶことにします.)ここで,![]() はプランク定数と呼ばれるようになったものです.このとき,エネルギーの平均値の計算は,次のように,積分が無限級数の和に置き換えられます.すなわち,
はプランク定数と呼ばれるようになったものです.このとき,エネルギーの平均値の計算は,次のように,積分が無限級数の和に置き換えられます.すなわち,
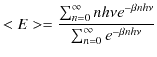
と表されます.この式の右辺を計算します.分母は,
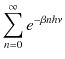 |
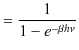 |
|
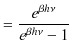 |
となり,分子は,
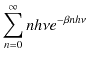 |
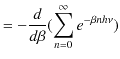 |
|
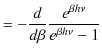 |
||
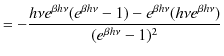 |
||
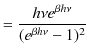 |
となります.したがって,1つの振動数 ![]() の状態について,エネルギー
の状態について,エネルギー ![]() の平均値は,
の平均値は,
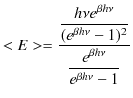
ですから,故に,
となります.
次に,![]() と
と ![]() の間に振動数をもつ固有状態の数を求めてみましょう.長さ
の間に振動数をもつ固有状態の数を求めてみましょう.長さ ![]() の1次元定常波の波長
の1次元定常波の波長 ![]() は,1次元弦の定常波と同様に,
は,1次元弦の定常波と同様に,
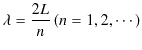
で与えられます.定常波の個数 ![]() を固有状態の数,あるいは簡単に状態数と呼ぶことにします.このとき,固有振動数は,
を固有状態の数,あるいは簡単に状態数と呼ぶことにします.このとき,固有振動数は,
となるので,状態数 ![]() は,
は,
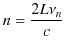
と表されます.ここで,3次元に拡張しましょう.黒体を1辺 ![]() の立方体とし,辺に沿って
の立方体とし,辺に沿って ![]() 軸,
軸,![]() 軸,
軸,![]() 軸をとります.このとき,黒体の中には定常波ができていますが,
軸をとります.このとき,黒体の中には定常波ができていますが,![]() 方向,
方向,![]() 方向,
方向,![]() 方向に投影された波が,弦の振動と同じ条件式を満たしていなければなりません.したがって,
方向に投影された波が,弦の振動と同じ条件式を満たしていなければなりません.したがって,![]() 方向,
方向,![]() 方向,
方向,![]() 方向へのそれぞれの波長は,次のように表されます.
方向へのそれぞれの波長は,次のように表されます.
ここで,
の関係があります.この(2.5)式を導くためには,方向余弦を使います.
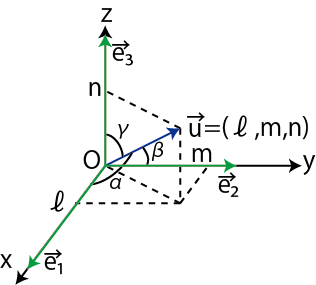
Figure2.1: 方向余弦
図の "方向余弦" のように,定常波の波面に垂直な方向への単位ベクトル
![]() をとります.単位ベクトルである基底ベクトルを,
をとります.単位ベクトルである基底ベクトルを,
![]() とし,
とし,![]() と各座標軸の正の向きとのなす角を,それぞれ
と各座標軸の正の向きとのなす角を,それぞれ
![]() とすると,
とすると,
となります.したがって,
ですが,
![]() は単位ベクトルですから,右辺は
は単位ベクトルですから,右辺は ![]() になります.故に,
になります.故に,
の関係が成立します.
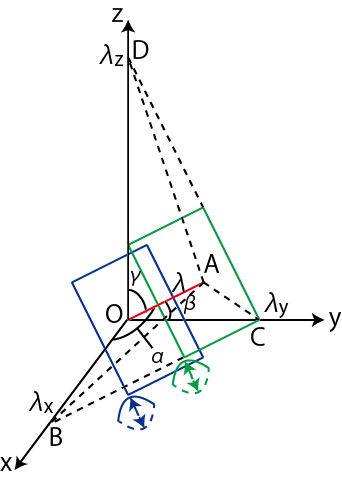
Figure2.2: 波長の関係
ここで,図の "波長の関係" を見て下さい.3次元空間における定常波の2つの波面を青色の4角形と緑色の4角形で示しています.状況を簡単にするため,青色の4角形の波面上に原点があるものとします.この2つの波面は,1波長 ![]() だけ離れています.(赤色の線の長さが
だけ離れています.(赤色の線の長さが ![]() です.)この
です.)この ![]() の
の ![]() 方向,
方向,![]() 方向,
方向,![]() 方向への投影成分を,それぞれ
方向への投影成分を,それぞれ
![]() としましたね.例えば,
としましたね.例えば,![]() 成分に着目しましょう.
成分に着目しましょう.
![]() ですが,3角形
ですが,3角形 ![]() において,
において,
![]() ですから,波長の間の関係が式で表せます.
ですから,波長の間の関係が式で表せます.![]() 成分と
成分と ![]() 成分もまとめておくと,
成分もまとめておくと,
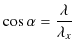 |
||
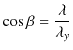 |
||
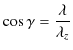 |
となります.これらの式を(2.6)式に代入すると,(2.5)式となります.(2.2)式,(2.3)式,(2.4)式を,(2.5)式に代入すると,波長 ![]() について,次のように計算されます.すなわち,
について,次のように計算されます.すなわち,
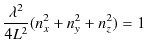 |
||
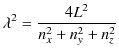 |
||
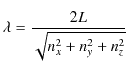 |
となります.状態数は,
![]() の組み合わせで数えられます.ここで,3次元空間で
の組み合わせで数えられます.ここで,3次元空間で ![]() 軸,
軸,![]() 軸,
軸,![]() 軸からなるデカルト座標系をとり,
軸からなるデカルト座標系をとり,
![]() の集まりからなる格子を考えます.(
の集まりからなる格子を考えます.(
![]() は自然数でしたね.)この座標系で,原点からの距離が
は自然数でしたね.)この座標系で,原点からの距離が ![]() と
と
![]() の間にある条件,
の間にある条件,
にかなう格子点の数は,![]() である限り,半径
である限り,半径 ![]() 及び
及び
![]() の球面で限られた球殻の
の球面で限られた球殻の ![]() の象限にある部分の体積にほぼ等しくなります.この体積は,
の象限にある部分の体積にほぼ等しくなります.この体積は,
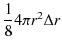
です.この体積の中にある格子点の数が,原点からの距離が ![]() と
と
![]() の間にある条件にかなう状態数になります.ここで,
の間にある条件にかなう状態数になります.ここで,
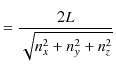 |
||
ですから,
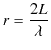 |
||
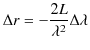 |
となります.よって,原点からの距離が ![]() と
と
![]() の間にある条件にかなう格子点の数は,
の間にある条件にかなう格子点の数は,
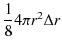 |
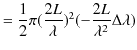 |
|
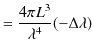 |
となります.さらに,関係式
![]() より,
より,
です.上記の格子点の数,すなわち,状態数は,
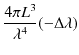 |
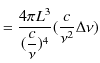 |
|
 |
となります.(
![]() は黒体の体積です.)ここで,電磁波は横波であるので,偏りは2種類あることに注意します.すなわち,状態数を2倍します.故に,
は黒体の体積です.)ここで,電磁波は横波であるので,偏りは2種類あることに注意します.すなわち,状態数を2倍します.故に,![]() を無限小にする極限をとると,
を無限小にする極限をとると,![]() と
と ![]() の間に固有振動数をもつ単位体積当たりの状態数は,
の間に固有振動数をもつ単位体積当たりの状態数は,
と求められます.
輻射の強度は1つの ![]() に対するエネルギーの平均値(2.1)式に,状態数(2.7)式を掛け合わせたものになります.
に対するエネルギーの平均値(2.1)式に,状態数(2.7)式を掛け合わせたものになります.
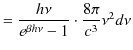 |
||
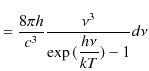 |
よって,プランクの公式,
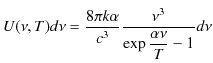
が導出することができました.ただし,
であることがわかります.以上の導出の核心は言うまでもなく,エネルギー量子仮説です.
プランクのエネルギー量子仮説により,連続な値をとるものとされていたエネルギーが,不連続な値をとることが判明しました.物質が原子的性質,つまり,跳び跳びの構造をもつことがわかったことに続いて,エネルギーもが跳び跳びの性質をもつことが理解されるようになったのです.この事実は19世紀の最後の年,1900年に発見されました.そして,それは20世紀の量子力学の成立へと繋がっていくのです.上記の ![]() はプランク定数でしたが,現在の精密な測定により次の値であることがわかっています.
はプランク定数でしたが,現在の精密な測定により次の値であることがわかっています.