Part1 量子力学へのあゆみ

Chapter1 原子的性質

1.1 原子的性質

全ての物質の根源的要素のことを元素といいます．現代において，元素とは原子の種類であると言えるでしょう．原子は原子核と電子から構成されていて，跳び跳びの構造をもつことが理解されています．この跳び跳びの構造をもつことを原子的性質と呼ぶことにしましょう．原子の多様な形態，結合により様々な物質が構成されています．近代の原子論の特徴は，物質というものが連続的な構造ではなく，跳び跳びの不連続な構造をもつことにあります．

 

1.2 電子の発見

ガラス管の中を真空に近い状態にして，高電圧をかけると放電現象が起こります．このとき見える線を陰極線といいますが，つぎのような特徴があります．

  1. 物体によって遮られ，影ができます．
  2. 負の電荷を運びます．
  3. 当たった物体の温度を上昇させます．（エネルギーを運びます．）
  4. 電場や磁場によって曲がります．

この陰極線の正体は何でしょうか？ 1897年，J.J.トムソンはトムソンの実験と呼ばれるもので，このことについて考察しました．

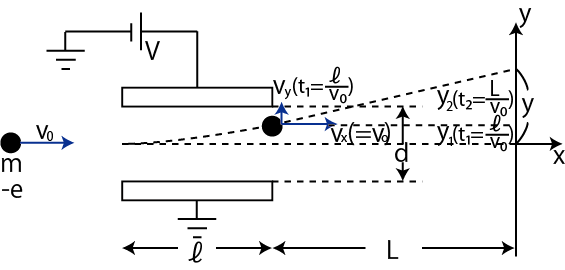
トムソンの実験

Figure1.1: トムソンの実験

実験装置は図の通りで，$ x$ 方向と $ y$ 方向をとります．そして，質量 $ m$，電荷 $ -e$ の陰極線の正体となる粒子を速さ $ v_{0}$ で入射します．長さ $ \ell$，間隔 $ d$ の極板間には $ V$ の電圧がかかっていて，電場が生じ，粒子の運動は曲げられます．極板から出た後は，力がはたらかないので，等速直線運動します．まず，極板間の運動を考えましょう．極板間を通過する間の時間変数を $ t_{1}$ としておきます．そして，粒子が極板の左端に入ってきた時刻を，$ t_{1}=0$ とします．$ x$ 方向には力を受けないので，慣性の法則より速さ $ v_{0}$ で等速運動します．したがって，極板の右端を出る時刻は， $ t_{1}=\frac{\ell}{v_{0}}$ であることがわかります．$ y$ 方向には電場から力を受けますが，運動方程式より，

  $\displaystyle ma_{y}=eE$    
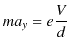% latex2html id marker 563 $\displaystyle \therefore$ $\displaystyle ma_{y}=e\dfrac{V}{d}$    
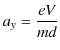% latex2html id marker 565 $\displaystyle \therefore$ $\displaystyle a_{y}=\dfrac{eV}{md}$    

の加速度で，等加速度運動をすることがわかります．このとき，関係式，

$\displaystyle v(t)=v_{0}+at$

より，

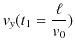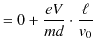$\displaystyle v_{y}(t_{1}=\dfrac{\ell}{v_{0}})$ $\displaystyle =0+\dfrac{eV}{md}\cdot\dfrac{\ell}{v_{0}}$    
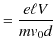  $\displaystyle =\dfrac{e\ell V}{mv_{0}d}$    

となります．また，関係式，

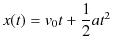
$\displaystyle x(t)=v_{0}t+\dfrac{1}{2}at^{2}$

より，極板間での $ y$ 方向の移動距離 $ y_{1}(t_{1}=\frac{\ell}{v_{0}})$ は，

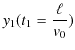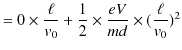$\displaystyle y_{1}(t_{1}=\dfrac{\ell}{v_{0}})$ $\displaystyle =0\times\dfrac{\ell}{v_{0}}+\dfrac{1}{2}\times\dfrac{eV}{md}\times(\dfrac{\ell}{v_{0}})^{2}$    
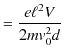  $\displaystyle =\dfrac{e\ell^{2}V}{2mv_{0}^{2}d}$    

となります．次に，極板間を出た後の運動について考えましょう．極板間を出た後の時間変数を $ t_{2}$ としておきます．そして，粒子が極板の右端を出た時刻を，$ t_{2}=0$ とします．粒子は $ x$ 方向についても，$ y$ 方向についても等速運動をします．図のように，極板の右端からスクリーンまでの $ x$ 方向の長さを $ L$ とすると，スクリーンに達する時刻は， $ t_{2}=\frac{L}{v_{0}}$ です．したがって，極板を出た後の $ y$ 方向の移動距離 $ y_{2}(t_{2}=\frac{L}{v_{0}})$ は，

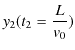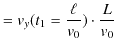$\displaystyle y_{2}(t_{2}=\dfrac{L}{v_{0}})$ $\displaystyle =v_{y}(t_{1}=\dfrac{\ell}{v_{0}})\cdot\dfrac{L}{v_{0}}$    
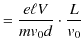  $\displaystyle =\dfrac{e\ell V}{mv_{0}d}\cdot\dfrac{L}{v_{0}}$    
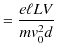  $\displaystyle =\dfrac{e\ell LV}{mv_{0}^{2}d}$    

となります．故に，

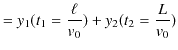$\displaystyle y$ $\displaystyle =y_{1}(t_{1}=\dfrac{\ell}{v_{0}})+y_{2}(t_{2}=\dfrac{L}{v_{0}})$    
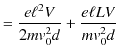  $\displaystyle =\dfrac{e\ell^{2}V}{2mv_{0}^{2}d}+\dfrac{e\ell LV}{mv_{0}^{2}d}$    
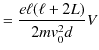  $\displaystyle =\dfrac{e\ell(\ell+2L)}{2mv_{0}^{2}d}V$    
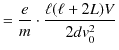  $\displaystyle =\dfrac{e}{m}\cdot\dfrac{\ell(\ell+2L)V}{2dv_{0}^{2}}$    

となります．ここで， $ y,\ell,L,V,d,v_{0}$ に測定値を代入して計算すると，陰極線の粒子の比電荷 $ \frac{e}{m}$ は，

$\displaystyle \dfrac{e}{m}=1.759\times10^{11}[C/kg]$

であることがわかりました．（値は，現在でのもの．）

　この比電荷の値は，当時知られていた陽イオンである水素イオンの比電荷に比べて約1800倍の値であることがわかります．陰極線の正体の粒子は，水素イオンと同じ質量で1800倍の大きさの負電荷をもつ粒子か，または，水素イオンと電荷の大きさは同じで $ 1/1800$ の質量をもつ粒子である可能性がありました．J.J.トムソンは後者をとり，その粒子を電子と名付けたのです．（電子の発見．）

 

1.3 電気素量の測定

トムソンの実験により，電子の電荷の大きさと質量の比である比電荷はわかったのですが，電子の電荷の大きさそのもの，あるいは電子の質量そのものは測定されていませんでした．1909年，ミリカンはミリカンの実験と呼ばれるもので，電子の電荷の大きさである電気素量の測定に成功しました．実験の概要を見ていきましょう．

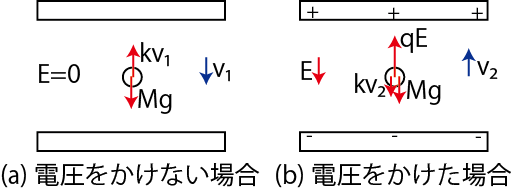
ミリカンの実験

Figure1.2: ミリカンの実験

微小な油滴を作り，それに電子数個を付着させます．油滴1個の質量を $ M$，電荷を $ -q$ とします．極板間に油滴を噴霧させます．ここで，図の(a)のように，電圧をかけない場合，重力 $ Mg$ と空気の抵抗力 $ kv_{1}$ がつりあい，油滴は速さ $ v_{1}$ で等速運動をします．つりあいの式は，

$\displaystyle kv_{1}=Mg$ (1.1)

です．次に，図の(b)のように，極板間に電圧をかけた場合，クーロン力 $ qE$，重力 $ Mg$，空気の抵抗力 $ kv_{2}$ がつりあい，油滴は速さ $ v_{2}$ で等速運動をします．つりあいの式は，

$\displaystyle qE=Mg+kv_{2}$

となり，

$\displaystyle kv_{2}=qE-Mg$ (1.2)

の式が成立します．ここで，(1.2)式÷(1.1)式を実行して，計算していきます．

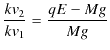  $\displaystyle \dfrac{kv_{2}}{kv_{1}}=\dfrac{qE-Mg}{Mg}$    
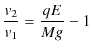% latex2html id marker 646 $\displaystyle \therefore$ $\displaystyle \dfrac{v_{2}}{v_{1}}=\dfrac{qE}{Mg}-1$    
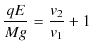% latex2html id marker 648 $\displaystyle \therefore$ $\displaystyle \dfrac{qE}{Mg}=\dfrac{v_{2}}{v_{1}}+1$    
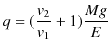% latex2html id marker 650 $\displaystyle \therefore$ $\displaystyle q=(\dfrac{v_{2}}{v_{1}}+1)\dfrac{Mg}{E}$    

最後の式から，油滴の電荷がわかり，それは電子の電荷数個分の電荷であるので，電子1個の電荷の大きさである，電気素量が求められたのです．電気素量 $ e$ は現在の精密な実験により，次の値になります．

$\displaystyle e=1.602\times10^{-19}[C]$

これと，電子の比電荷の値をあわせて，電子の質量も計算できます．

$\displaystyle m$ $\displaystyle =\dfrac{m}{e}\cdot e$    
  $\displaystyle =\dfrac{1}{1.75882012\times10^{11}[C/kg]}\times1.60217653\times10^{-19}[C]$    
  $\displaystyle =0.910938\cdots\times10^{-30}$    
  $\displaystyle \cong9.109\times10^{-31}[kg]$    

　電子の発見，及び，電気素量の測定によって，物質は跳び跳びの構造もっており，原子的性質を備えていることが確立されました．これらの研究は19世紀の終わりから20世紀の初めにかけて行われ，量子力学が創始される時代の幕開けの準備となりました．