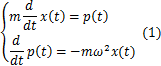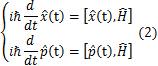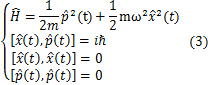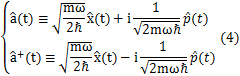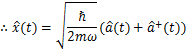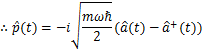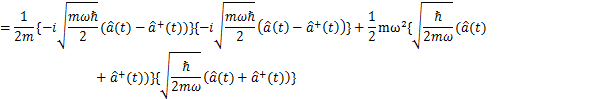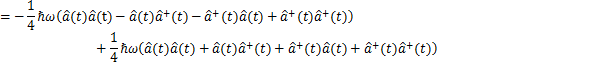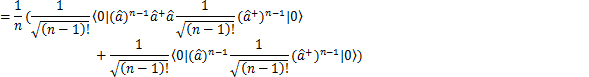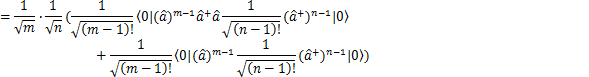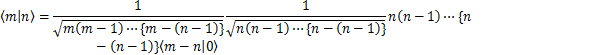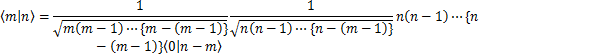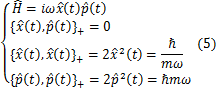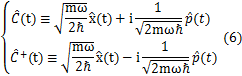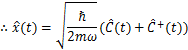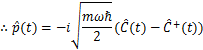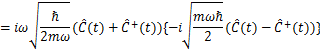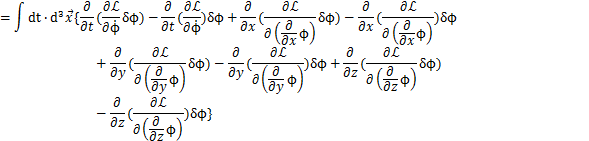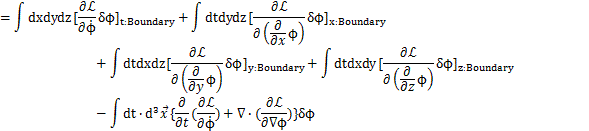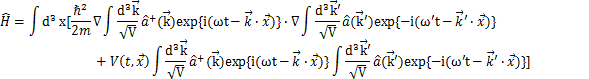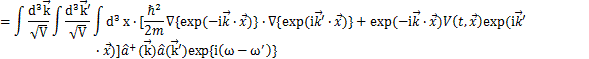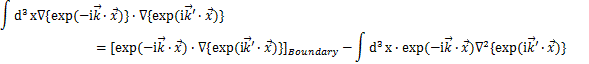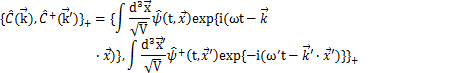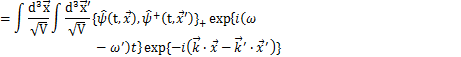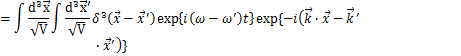J Simplicity 波動場の正準量子化（第二量子化）

Chapter22 波動場の正準量子化（第二量子化）

22.1 波動場の正準量子化とハイゼンベルク方程式

量子力学を発展させて素粒子論や物性理論へ進んだ場合，場を量子化する必要性が生じてきます．場といえば，電磁場がすぐに思いつきますが，時間と空間に依存した物理量で，物理的に意味のあるものならば，考えるべき対象となります．例えば，時間と空間に依存する量である波動関数も，場であるということが言えます．それ以外に，特殊相対論的量子力学で登場してくる方程式を満たす場も取り扱います．（詳しくは場の量子論のReportで取り扱います．）それらの場を量子化する場合，物理量すなわちオブザーバブルである場を，量子力学の一般論に従い，演算子に格上げします．演算子に格上げされた場は，フーリエ展開されると，その展開係数が，ある代数的関係を満たします．その代数的関係というのが，調和振動子の代数学です．以下のSectionで見ていくように，場の量は，調和振動子の代数学を満たす生成消滅演算子と呼ばれるもので表されることになります．
　場の量子化を扱うこのChapterでは，ハイゼンベルク描像で議論を進めます．この描像ではオブザーバブルが時間的に変化し，ケットやブラの量子状態には時間依存性がありません．このとき，基礎方程式であるハイゼンベルク方程式が成立します．

は一般的なオブザーバブル，はハミルトニアンを表します．また，右辺の括弧は交換子で，

と定義されるもので，文字の上の記号ハットはその量が演算子であることを示しています．
　ハイゼンベルク方程式を基礎にして，量子化を実行する方法について，調和振動子を考えてみましょう．調和振動子の座標をx，その角振動数をωとすると，古典論での運動方程式は，

です．この方程式は，

と同等になります．(1)式が，ハイゼンベルク方程式，

と一致するように，ハミルトニアンと，の満たす代数関係を同時に決めてみましょう．(1)式は古典論の方程式，(2)式は量子力学の方程式です．代数関係を決定することで，量子化を実現することができるのです．何故なら，x(t),p(t)が量子化される前は，ただの数です(c-数といいます．)が，それらが，代数関係を設定した後では演算子になっているからです．（q-数といいます．演算子は作用の順番が意味を持つのでしたね．ですから，代数関係によって，c-数を，演算子であるq-数に格上げできるのです．）代数関係を設定することにより，実行される量子化のことを正準量子化といいます．次の２つのSectionで，２通りの場合について考えてみます．

22.2 調和振動子の代数学と生成消滅演算子１: ボゾンの場合

最初の設定として，

として量子化する場合を考えます．これらは，通常の調和振動子のハミルトニアンと量子力学一般に成立する交換関係です．この交換関係が，代数関係になります．ここで，ハイゼンベルク方程式(2)式を使って，古典的な方程式(1)式の関係を量子化したものが導出されることを確認しておきます．

　

　

　

　

　

　

　

　

　

　

確かに，(1)式の関係を量子化したものが導出されました．
　(3)式のような交換関係による量子化は，通常の調和振動子を正準変数で量子化したものと同じであり，ハミルトニアンは，固有値，

をもちました．（Report “量子力学１”のChapter “束縛状態:例（調和振動子）”を参照されてください．）ここで，

を定義して新しい演算子を導入します．右辺の係数が気になりますが，(4)式は，Chapter “束縛状態:例（調和振動子）”のSection ”演算子法による解法”で出てきた式と全く同じです．(3)式の交換関係を使って計算すると，

となります．また，

は，明らかに成立します．(4)式の逆変換も計算しておきます．(4)式の２つの式を辺々足して，

となります．(4)式の２つの式を辺々引くと，

となります．
　演算子はボーズ演算子といいますが，その性質をみておくことにしましょう．まず，(3)式のハミルトニアンを計算します．

　

　

　

　

　

と表されます．ここで，ボーズ演算子に対して，ハイゼンベルク方程式，

を適用して，その時間依存性を調べてみます．

　

　

　

ここで，

と定義すると，

となります．さらに，この式の両辺の複素共役をとると，

となります．についての交換関係の式で，t=0とおいて，についての交換関係，

が成立します．話をハミルトニアンに戻しましょう．調和振動子のエネルギー固有値は，

でしたので，演算子は，固有値をもつことがわかります．そこで，演算子を個数演算子，

として定義しましょう．このとき，

　

となって，個数演算子は時間に依存しません．したがって，の固有値nも時間には無関係になります．さらに，固有状態をと表しますが，ハイゼンベルク描像では状態ベクトルは無条件に時間に依存しません．結局，固有方程式は，

と表せますが，全てのパーツが時間に依りません．そこで，以下このSectionでは，ボーズ演算子は，ではなく，時間に依存しないを使うことにします．
　さて，次の計算をします．

となります．確かに，nは0または正であることが確認されました．また，

したがって，状態はの固有状態で，n-1の固有値をもちます．演算子は個数演算子の固有値を１つ減らす働きをもつことになりましたので，消滅演算子といいます．消滅演算子を繰り返し状態に作用させていくと，その固有値はいずれ0になります．（の性質があるので，負の固有値はありません．）固有値0の状態を真空状態といい，記号で表し，次式で定義します．

さらに，規格化条件，

も成立するとしておきます．このとき，

となります．つまり，真空状態の個数演算子の固有値は0になります．（粒子数が0の状態が真空状態です．）演算子の性質も調べましょう．

したがって，状態はn+1の固有値をもちます．演算子は個数演算子の固有値を１つ増やす働きをもつことになりましたので，生成演算子といいます．
　ここで，生成演算子をn回だけ真空状態に作用させると，粒子がn個生成されますので，固有状態をつくることができます．規格化条件まで考慮して，

とします．このとき，固有方程式が成立することが，次のように確認されます．

次のように，規格化条件も成立します．

直交条件も成立します．m≠nのとき，

となります．m>nの場合，

となります．ただし，最後の変形は，真空の定義式，

を使いました．一方，m<nの場合，

となります．ただし，最後の変形は，真空の定義式のエルミート共役をとった式，

を使いました．まとめて，規格直交条件，

と表しておきます．ただし，右辺の記号はクロネッカのデルタ，

です．
　生成消滅演算子を用いて，個数演算子の固有値nの数を１つずつ増減できます．したがって，固有値nの数を粒子数とみなすことができます．場の量子論において，粒子は生まれたり，消えたりする量になります．このように，交換関係が成立する生成消滅演算子については，粒子数が0から無限大になります．この場合，粒子はボゾンです．
　実際のボーズ粒子は運動量をもっていますから，そのような場合に応用できるように，代数を拡張しておきます．すなわち，演算子をとしておきます．このとき，交換関係は，

となります．拡張された個数演算子，

の固有値は，

であり，規格直交する状態ベクトルは，

　

で与えられます．この状態ベクトルの空間をフォック空間といいます．ただし，ケットベクトルは真空状態で，

を満たします．

22.3 調和振動子の代数学と生成消滅演算子２: フェルミオンの場合

調和振動子の運動方程式(1)式が，ハイゼンベルク方程式(2)と一致するような２番目の量子化の方法として，

と設定してみましょう．ただし，

と定義される括弧は，反交換子と呼ばれる記号です．したがって，(5)の３つの式からなる代数関係は，反交換関係といいます．(5)式のハミルトニアンも反交換関係も，(3)式のものとは全く異なるものです．しかし，ハイゼンベルク方程式(2)式を計算してみると，調和振動子の方程式(1)式を量子化したものに一致することが，以下のように確認されます．

　

　

　

　

　

　

　

　

　

　

　

　

確かに，(1)式の関係を量子化したものが導出されました．
　また，

　

　

　

　

　

と，なります．したがって，ハミルトニアンの固有値は，

すなわち，

と表せます．ここで，(4)式と同様に，

と，新しい演算子を定義します．このとき，

が，成立します．(6)式の逆変換も計算しておきます．(6)式の２つの式を辺々足して，

となります．(6)式の２つの式を辺々引くと，

となります．
　演算子はフェルミ演算子といいますが，その性質をみておくことにしましょう．まず，(5)式のハミルトニアンを計算します．

　

　

　

　

　

と表されます．ここで，フェルミ演算子に対して，ハイゼンベルク方程式，

を適用して，その時間依存性を調べてみます．

　

　

　

　

　

ここで，

と定義すると，

となります．さらに，この式の両辺の複素共役をとると，

となります．についての反交換関係の式で，t=0とおいて，についても反交換関係，

が成立します．話をハミルトニアンに戻しましょう．エネルギー固有値は先程，求めたように，

でしたので，演算子は，固有値n(=0,1)をもつことがわかります．そこで，演算子を個数演算子，

として定義しましょう．このとき，

　

　

となって，個数演算子は時間に依存しません．したがって，個数演算子の固有値nも時間には無関係になります．さらに，固有状態をと表しますが，ハイゼンベルク描像では状態ベクトルは無条件に時間に依存しません．結局，固有方程式は，

と表せますが，全てのパーツが時間に依りません．そこで，以下このSectionでは，フェルミ演算子は，ではなく，時間に依存しないを使うことにします．
　さて，次の計算をします．

と，なります．故に，nは0または正です．また，

したがって，状態はn-1の固有値をもちます．演算子は個数演算子の固有値を１つ減らす働きをもつことになりましたので，消滅演算子といいます．消滅演算子を繰り返し状態に作用させていくと，その固有値はいずれ0になります．（の性質があるので，負の固有値はありません．）固有値0の状態を真空状態といい，記号で表し，次式で定義します．

さらに，規格化条件，

も成立するとしておきます．このとき，

となります．つまり，真空状態の個数演算子の固有値は0になります．（粒子数が0の状態が真空状態です．）演算子の性質も調べましょう．

したがって，状態はn+1の固有値をもちます．演算子は個数演算子の固有値を１つ増やす働きをもつことになりましたので，生成演算子といいます．生成消滅演算子を用いて，個数演算子の固有値nの数を１つずつ増減できます．固有値nの数を粒子数とみなすことができます．場の量子論において，粒子は生まれたり，消えたりする量になります．
　さらに，

　

　

　

となります．したがって，個数演算子の固有値nは0または1の値をとり，固有状態は，またはのどちらかであるという定理が証明されました．以下のような関係式も導出することができます．

このように，反交換関係が成立する生成消滅演算子においては，粒子数が0または1になります．この場合のパウリ原理を満たす粒子はフェルミオンです．
　実際のフェルミオンは運動量をもっていますから，そのような場合に応用できるように，代数を拡張しておきます．すなわち，演算子をとしておきます．このとき，反交換関係は，

となります．拡張された個数演算子，

の固有値は，

であり，規格直交する状態ベクトルは，

で与えられます．は0か1なので，ボゾンの場合に必要だった規格化因子，

は不要です．上の状態ベクトルの空間をフォック空間といいます．ただし，ケットベクトルは真空状態で，

を満たします．

22.4 場の古典論と波動場の正準量子化

場の量子化の準備として，古典場の解析力学を取り扱っておきましょう．古典場を一般に，と表しておきます．そして，系のラグランジアンLをラグランジアン密度で表します．（は場の時間微分です．）すなわち，を空間３次元について積分して，

とします．（．）さらに，ラグランジアンLを時間で積分した量を作用Sといいます．

ここで，ある領域Ωに対して，場を，

となるように，変化させます．ただし，領域の境界で，

が成立するものとします．場が上述のように変わるとき，作用Sは，

と表記されますが，

となることを自然は要求します．言い直すと，作用Sを最小にするように自然はできているのです．この原理を最小作用の原理と言います．ここで，左辺を次のように計算します．

　

ここで，右辺第２，第３項は，

最後の変形には境界面において，

であることを使いました．よって，

　

となります．任意のについて，この式が成立するためには，被積分が0にならなければなりません．故に，

が成立します．この場の方程式をオイラー-ラグランジュ方程式と言います．
　次に，ハミルトニアンについて見ておきます．通常の解析力学を場について拡張した議論を行います．まず，場の共役運動量密度πを，

で定義します．更に，ハミルトニアン密度を定義します．

このハミルトニアン密度から，ハミルトニアンHが計算されます．すなわち，

から求められます．
　場の古典論は以上にして，次に，場を量子化する方法について考えましょう．量子論ではオブザーバブルは演算子で表されることになります．場を演算子に格上げした瞬間に，場の量子化が実行されたことになります．この際，演算子は積の順序が問題となりますので，交換関係を設定することになります．このような交換関係による量子化のことを正準量子化といいます．量子力学での位置演算子と運動量演算子の間の交換関係，

を参考にして，場φとその一般化運動量πの間に次の同時刻交換関係を設定します．

と設定します．場は空間に対して連続量なので，第１式の右辺ではデルタ関数が使われています．注意すべきことは，これらの同時刻交換関係による正準量子化はボソンについて適用されるということです．フェルミオンについては，次の同時刻反交換関係を設定します．

　一般的な場についての議論は以上です．次のSectionから，具体的な場としてシュレディンガー場について見ていきます．

22.5 シュレディンガー場の古典論

具体的に量子化すべき場には，電磁場や特殊相対論的量子力学の方程式に従う場などがあります．これらはReport “場の量子論” で取り扱っていきます．（Chapter ”Klein-Gordon場”，”Dirac場”，”Maxwell場” を見て下さい．）その前に，最初に取り上げる例として，シュレディンガー方程式に従う波動関数を取り上げましょう．波動関数については，既に量子化が完了しているのではないかと考える人も多いと思います．確かに，E=Hという古典論の方程式を量子化してシュレディンガー方程式，

を導きました．ここではさらに，時間と空間の関数である，すなわち場である波動関数を，演算子に格上げして量子化するのです．ですから，この場合，２回量子化することになりますね．この２回目の量子化，つまり場の量子化のことを第二量子化といいます．そして，場としての波動関数のことをシュレディンガー場といいます．第二量子化する前のシュレディンガー場は，古典場であることに注意しておきましょう．
　第二量子化の準備として，シュレディンガー場の古典論を論じていきます．まず，ラグランジアン密度を，

としておきます．いきなり与えられましたので，この式はどこから導かれたのだろうと思われると思います．実は，ラグランジアン密度は，そのオイラー-ラグランジュ方程式が場の方程式，この場合シュレディンガー方程式，になるように発見されたのです．それでは，前Sectionのオイラー-ラグランジュ方程式において，一般の場をシュレディンガー場に置き換えた式，