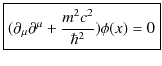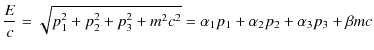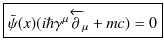Chapter23 特殊相対論的量子力学

23.1 クライン-ゴルドン方程式

古典論とは量子化していない物理を意味します．したがって，相対性理論は古典論になります．しかし，古典物理学という用語を使用する場合は，19世紀までの物理学を指し，相対性理論は現代物理学の範疇に属するものとします．量子論の基礎方程式であるシュレディンガー方程式は，古典力学の関係式 $ E=H$ を量子化して得られるものでした．ここで，特殊相対性理論と量子力学を融合する問題を考えてみましょう．特殊相対性理論の基礎的な関係式，

$\displaystyle E^{2}=c^{2}p^{2}+m^{2}c^{4}$ (23.1)

すなわち，

$\displaystyle E^{2}=c^{2}(p_{x}^{2}+p_{y}^{2}+p_{z}^{2})+m^{2}c^{4}$

において，物理量を次のように演算子で置き換えて量子化します．

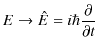  $\displaystyle E\to\hat{E}=i\hbar\dfrac{\partial}{\partial t}$    
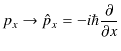  $\displaystyle p_{x}\to\hat{p}_{x}=-i\hbar\dfrac{\partial}{\partial x}$    
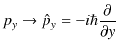  $\displaystyle p_{y}\to\hat{p}_{y}=-i\hbar\dfrac{\partial}{\partial y}$    
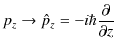  $\displaystyle p_{z}\to\hat{p}_{z}=-i\hbar\dfrac{\partial}{\partial z}$    

このとき，

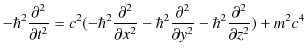  $\displaystyle -\hbar^{2}\dfrac{\partial^{2}}{\partial t^{2}}=c^{2}(-\hbar^{2}\d... ...^{2}}{\partial y^{2}}-\hbar^{2}\dfrac{\partial^{2}}{\partial z^{2}})+m^{2}c^{4}$    
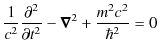% latex2html id marker 1044 $\displaystyle \therefore$ $\displaystyle \dfrac{1}{c^{2}}\dfrac{\partial^{2}}{\partial t^{2}}-\bm{\nabla}^{2}+\dfrac{m^{2}c^{2}}{\hbar^{2}}=0$    

となりますが，この演算子の関係を状態 $ \phi(ct,\bm{x})$ に作用させます．

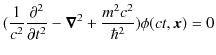
$\displaystyle (\dfrac{1}{c^{2}}\dfrac{\partial^{2}}{\partial t^{2}}-\bm{\nabla}^{2}+\dfrac{m^{2}c^{2}}{\hbar^{2}})\phi(ct,\bm{x})=0$

この特殊相対論的量子力学の基礎方程式をクライン-ゴルドン方程式といいます．

　ここで，特殊相対性理論の表記方法を導入しましょう．つまり，座標ベクトルは，反変ベクトルを，

$\displaystyle x$ $\displaystyle \equiv x^{\mu}$    
  $\displaystyle =(x^{0},x^{1},x^{2},x^{3})$    
  $\displaystyle =(ct,x,y,z)$    
  $\displaystyle =(ct,\bm{x})$    

として，共変ベクトルを，

$\displaystyle x_{\mu}$ $\displaystyle =\eta_{\mu\nu}x^{\nu}$    
  $\displaystyle =(x^{0},-x^{1},-x^{2},-x^{3})$    
  $\displaystyle =(ct,-x,-y,-z)$    
  $\displaystyle =(ct,-\bm{x})$    

とします． $ \eta_{\mu\nu}$ は計量テンソルで，

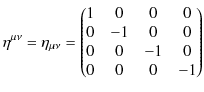
$\displaystyle \eta^{\mu\nu}=\eta_{\mu\nu}= \begin{pmatrix} 1&0&0&0\\ 0&-1&0&0\\ 0&0&-1&0\\ 0&0&0&-1 \end{pmatrix}$

と定義します．計量テンソルによって，添え字の上げ下げができます．また，

$\displaystyle \partial_{\mu}$ $\displaystyle =\dfrac{\partial}{\partial x^{\mu}}$    
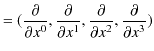  $\displaystyle =(\dfrac{\partial}{\partial x^{0}},\dfrac{\partial}{\partial x^{1}},\dfrac{\partial}{\partial x^{2}},\dfrac{\partial}{\partial x^{3}})$    
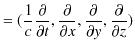  $\displaystyle =(\dfrac{1}{c}\dfrac{\partial}{\partial t},\dfrac{\partial}{\partial x},\dfrac{\partial}{\partial y},\dfrac{\partial}{\partial z})$    
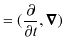  $\displaystyle =(\dfrac{\partial}{\partial t},\bm{\nabla})$    

と，

$\displaystyle \partial^{\mu}$ $\displaystyle =\dfrac{\partial}{\partial x_{\mu}}$    
  $\displaystyle =(\dfrac{\partial}{\partial x_{0}},\dfrac{\partial}{\partial x_{1}},\dfrac{\partial}{\partial x_{2}},\dfrac{\partial}{\partial x_{3}})$    
  $\displaystyle =(\dfrac{1}{c}\dfrac{\partial}{\partial t},-\dfrac{\partial}{\partial x},-\dfrac{\partial}{\partial y},-\dfrac{\partial}{\partial z})$    
  $\displaystyle =(\dfrac{\partial}{\partial t},-\bm{\nabla})$    

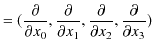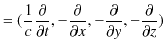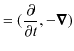という微分演算子を導入します．これらの演算子の縮約をとると，

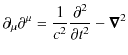
$\displaystyle \partial_{\mu}\partial^{\mu}=\dfrac{1}{c^{2}}\dfrac{\partial^{2}}{\partial t^{2}}-\bm{\nabla}^{2}$

となります．このとき，クライン-ゴルドン方程式は，

$\displaystyle \fbox{$(\partial_{\mu}\partial^{\mu}+\dfrac{m^{2}c^{2}}{\hbar^{2}})\phi(x)=0$}$ (23.2)

と表せます．

 

23.2 ディラック方程式

特殊相対性理論の基礎的な関係式(23.1)式，

$\displaystyle E^{2}=c^{2}p^{2}+m^{2}c^{4}$

を，もう1つ別の方法で量子化して，ディラック方程式と呼ばれる2つ目の特殊相対論的量子力学の基礎方程式を導きましょう．(23.1)式を運動量について1次式で表し，次式のようにおいてみます．

$\displaystyle \dfrac{E}{c}=\sqrt{p_{1}^{2}+p_{2}^{2}+p_{3}^{2}+m^{2}c^{2}}=\alpha_{1}p_{1}+\alpha_{2}p_{2}+\alpha_{3}p_{3}+\beta mc$ (23.3)

ただし，

  $\displaystyle p_{1}=p_{x}$    
  $\displaystyle p_{2}=p_{y}$    
  $\displaystyle p_{3}=p_{z}$    

です．(23.3)式を2乗すると，次のようになります．

$\displaystyle p_{1}^{2}+p_{2}^{2}+p_{3}^{2}+m^{2}c^{2}$ $\displaystyle =\alpha_{1}^{2}p_{1}^{2}+\alpha_{2}^{2}p_{2}^{2}+\alpha_{3}^{2}p_{3}^{2}+\beta^{2}m^{2}c^{2}$    
  $\displaystyle \,\,\,+(\alpha_{1}\alpha_{2}+\alpha_{2}\alpha_{1})p_{1}p_{2}+(\al... ..._{3}\alpha_{2})p_{2}p_{3}+(\alpha_{3}\alpha_{1}+\alpha_{1}\alpha_{3})p_{3}p_{1}$    
  $\displaystyle \,\,\,+(\alpha_{1}\beta+\beta\alpha_{1})p_{1}mc+(\alpha_{2}\beta+\beta\alpha_{2})p_{2}mc+(\alpha_{3}\beta+\beta\alpha_{3})p_{3}mc$    

この式をもとの(23.1)式と比較すると， $ \alpha_{i}$ と $ \beta$ は次の関係式を満たさなければなりません．

  $\displaystyle \alpha_{1}^{2}=\alpha_{2}^{2}=\alpha_{3}^{2}=\beta^{2}=1$ (23.4)
  $\displaystyle \alpha_{i}\alpha_{j}+\alpha_{j}\alpha_{i}=0\,(i,j=1,2,3,i\neq j)$ (23.5)
  $\displaystyle \alpha_{i}\beta+\beta\alpha_{i}=0\,(i=1,2,3)$ (23.6)

(23.3)式の両辺を $ c$ 倍した式，

$\displaystyle E=\alpha_{1}cp_{1}+\alpha_{2}cp_{2}+\alpha_{3}cp_{3}+\beta mc^{2}$

を量子化しましょう．すなわち，次のようにエネルギーと運動量を演算子に置き換えます．

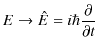  $\displaystyle E\to\hat{E}=i\hbar\dfrac{\partial}{\partial t}$    
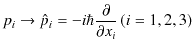  $\displaystyle p_{i}\to\hat{p}_{i}=-i\hbar\dfrac{\partial}{\partial x_{i}}\,(i=1,2,3)$    

このとき，

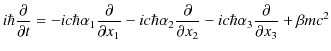  $\displaystyle i\hbar\dfrac{\partial}{\partial t}=-ic\hbar\alpha_{1}\dfrac{\part... ...{\partial x_{2}}-ic\hbar\alpha_{3}\dfrac{\partial}{\partial x_{3}}+\beta mc^{2}$    
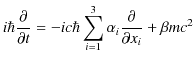% latex2html id marker 1104 $\displaystyle \therefore$ $\displaystyle i\hbar\dfrac{\partial}{\partial t}=-ic\hbar\sum_{i=1}^{3}\alpha_{i}\dfrac{\partial}{\partial x_{i}}+\beta mc^{2}$    

となりますが，この演算子の関係式を状態 $ \psi(x)$ に作用させます．

$\displaystyle i\hbar\dfrac{\partial}{\partial t}\psi(x)=(-ic\hbar\sum_{i=1}^{3}\alpha_{i}\dfrac{\partial}{\partial x_{i}}+\beta mc^{2})\psi(x)$ (23.7)

この(23.7)式をディラック方程式といいます．ここで， $ \alpha_{i}$ と $ \beta$ は(23.4)式，(23.5)式，(23.6)式を満たさなければなりません．この条件を満足するのは，普通の数ではなく，次のディラック行列と呼ばれる $ 4\times4$ 行列です．

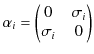  $\displaystyle \alpha_{i}= \begin{pmatrix} 0&\sigma_{i}\\ \sigma_{i}&0 \end{pmatrix}$    
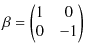  $\displaystyle \beta= \begin{pmatrix} 1&0\\ 0&-1 \end{pmatrix}$    

ここで，$ \sigma$ は $ 2\times2$ のパウリ行列，$ 1$ と記してあるのは $ 2\times2$ 単位行列です．また，状態 $ \psi(x)$ は $ 4\times1$ のスピノルと呼ばれる量です．

 

23.3 γ行列

ディラック方程式をシンプルな形で表現するために，γ行列と呼ばれる行列を，次のように定義して導入します．

$\displaystyle \gamma^{\mu}=(\gamma^{0},\gamma^{i})\equiv(\beta,\beta\alpha_{i})\,(i=1,2,3)$

このとき，γ行列は次の関係式を満たします．

$\displaystyle \{\gamma^{\mu},\gamma^{\nu}\}=2\eta^{\mu\nu}$ (23.8)

ただし，左辺の括弧は反交換子で，

$\displaystyle \{A,B\}\equiv AB+BA$

で定義される記号で，右辺の $ \eta^{\mu\nu}$ は次の式で定義される行列です．

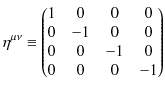
$\displaystyle \eta^{\mu\nu}\equiv \begin{pmatrix} 1&0&0&0\\ 0&-1&0&0\\ 0&0&-1&0\\ 0&0&0&-1 \end{pmatrix}$

ここで，$ 1$ は $ 4\times4$ 単位行列を表します．(23.8)式の導出は次の通りです．第0成分どうしの反交換関係は，

$\displaystyle \{\gamma^{0},\gamma^{0}\}$ $\displaystyle =\gamma^{0}\gamma^{0}+\gamma^{0}\gamma^{0}$    
  $\displaystyle =2\gamma^{0}\gamma^{0}$    
  $\displaystyle =2\beta^{2}$    
  $\displaystyle =2\cdot1$    

です．第0成分と第 $ i$ 成分の反交換関係は，

$\displaystyle \{\gamma^{0},\gamma^{i}\}$ $\displaystyle =\gamma^{0}\gamma^{i}+\gamma^{i}\gamma^{0}$    
  $\displaystyle =\beta\cdot\beta\alpha_{i}+\beta\alpha_{i}\cdot\beta$    
  $\displaystyle =\beta(\beta\alpha_{i}+\alpha_{i}\beta)$    
  $\displaystyle =0$    

です．第 $ i$ 成分と第 $ j$ 成分の反交換関係は，

$\displaystyle \{\gamma^{i},\gamma^{j}\}$ $\displaystyle =\gamma^{i}\gamma^{j}+\gamma^{j}\gamma^{i}$    
  $\displaystyle =\beta\alpha_{i}\beta\alpha_{j}+\beta\alpha_{j}\beta\alpha_{i}$    
  $\displaystyle =-\alpha_{i}\beta\beta\alpha_{j}-\alpha_{j}\beta\beta\alpha_{i}$    
  $\displaystyle =-\alpha_{i}\alpha_{j}-\alpha_{j}\alpha_{i}$    
  $\displaystyle =2(-\delta_{ij})$    

となります．ただし，(23.4)式，(23.5)式，(23.6)式を使いました．また，γ行列は次の関係式も満たします．

$\displaystyle \gamma^{0}(\gamma^{\mu})^{\dagger}\gamma^{0}=\gamma^{\mu}$ (23.9)

(23.9)式の導出は次の通りです．第0行列は，

$\displaystyle (\gamma^{0})^{\dagger}$ $\displaystyle =\beta^{\dagger}$    
  $\displaystyle =\beta$    
  $\displaystyle =\gamma^{0}$    

ですから，

$\displaystyle \gamma^{0}(\gamma^{0})^{\dagger}\gamma^{0}$ $\displaystyle =\gamma^{0}\gamma^{0}\gamma^{0}$    
  $\displaystyle =1\cdot\gamma^{0}$    
  $\displaystyle =\gamma^{0}$    

となります．第 $ i$ 行列 $ (i=1,2,3)$ は，

$\displaystyle (\gamma^{i})^{\dagger}$ $\displaystyle =(\beta\alpha_{i})^{\dagger}$    
  $\displaystyle =\alpha_{i}^{\dagger}\beta^{\dagger}$    
  $\displaystyle =\alpha_{i}\beta$    
  $\displaystyle =-\beta\alpha_{i}$    
  $\displaystyle =-\gamma^{i}$    

ですから，

$\displaystyle \gamma^{0}(\gamma^{i})^{\dagger}\gamma^{0}$ $\displaystyle =\gamma^{0}(-\gamma^{i})\gamma^{0}$    
  $\displaystyle =\gamma^{0}\gamma^{0}\gamma^{i}$    
  $\displaystyle =1\cdot\gamma^{i}$    
  $\displaystyle =\gamma^{i}$    

となります．（証明終．）

　γ行列を使って，ディラック方程式(23.7)式，

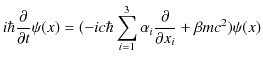
$\displaystyle i\hbar\dfrac{\partial}{\partial t}\psi(x)=(-ic\hbar\sum_{i=1}^{3}\alpha_{i}\dfrac{\partial}{\partial x_{i}}+\beta mc^{2})\psi(x)$

をシンプルに表しておきましょう．次のように変形していきます．

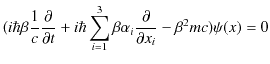  $\displaystyle (i\hbar\beta\dfrac{1}{c}\dfrac{\partial}{\partial t}+i\hbar\sum_{i=1}^{3}\beta\alpha_{i}\dfrac{\partial}{\partial x_{i}}-\beta^{2}mc)\psi(x)=0$    
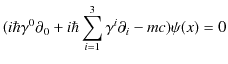% latex2html id marker 1198 $\displaystyle \therefore$ $\displaystyle (i\hbar\gamma^{0}\partial_{0}+i\hbar\sum_{i=1}^{3}\gamma^{i}\partial_{i}-mc)\psi(x)=0$    

したがって，

$\displaystyle \fbox{$(i\hbar\gamma^{\mu}\partial_{\mu}-mc)\psi(x)=0$}$ (23.10)

と表せます．さらに，ディラック方程式は次のようにも表せます．(23.10)式において，両辺のエルミート共役をとり，計算します．（ $ \overleftarrow{\mathrm{\partial}}_{\mu}$ は左に演算する微分演算子です．）

  $\displaystyle \psi^{\dagger}(x)\{-i\hbar(\gamma^{\mu})^{\dagger}\overleftarrow{\mathrm{\partial}}_{\mu}-mc\}=0$    
% latex2html id marker 1205 $\displaystyle \therefore$ $\displaystyle \psi^{\dagger}(x)\gamma^{0}\gamma^{0}\{i\hbar(\gamma^{\mu})^{\dagger}\overleftarrow{\mathrm{\partial}}_{\mu}\gamma^{0}+mc\gamma^{0}\}=0$    
% latex2html id marker 1207 $\displaystyle \therefore$ $\displaystyle \psi^{\dagger}(x)\gamma^{0}\{i\hbar\gamma^{0}(\gamma^{\mu})^{\dagger}\gamma^{0}\overleftarrow{\mathrm{\partial}}_{\mu}+mc\gamma^{0}\gamma^{0}\}=0$    

ここで，

$\displaystyle \bar{\psi}(x)\equiv\psi^{\dagger}(x)\gamma^{0}$

とおき，(23.9)式と(23.8)式を使うと，

$\displaystyle \fbox{$\bar{\psi}(x)(i\hbar\gamma^{\mu}\overleftarrow{\mathrm{\partial}}_{\mu}+mc)=0$}$ (23.11)

が導かれます．