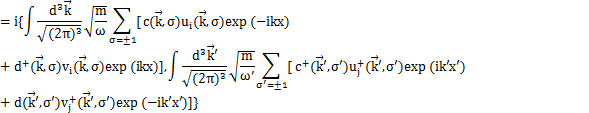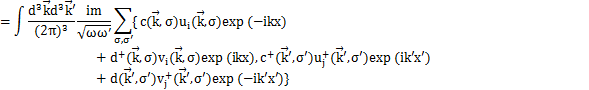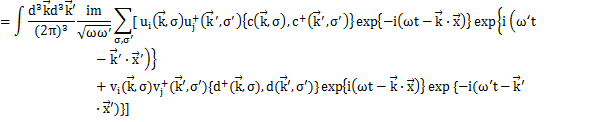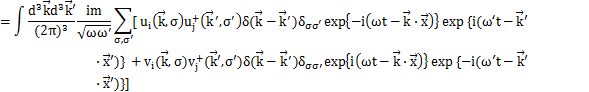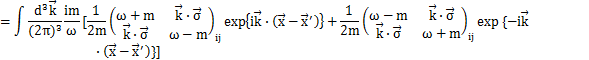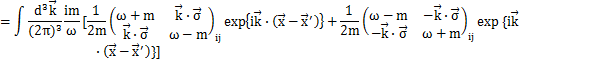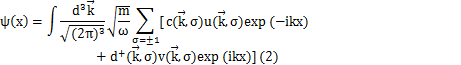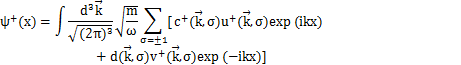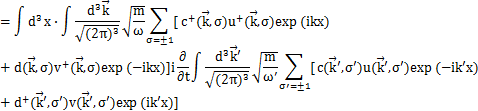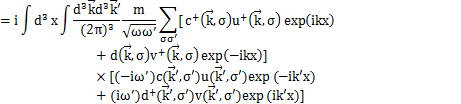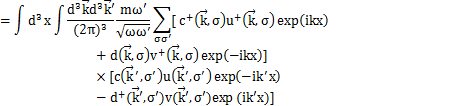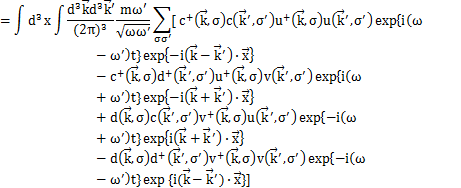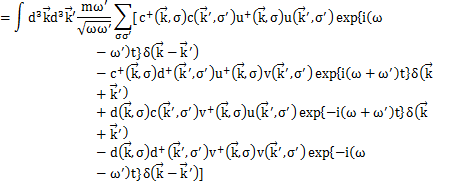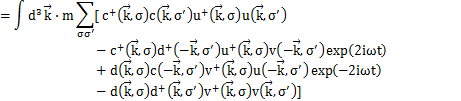3.1 Dirac場の古典論

特殊相対論的量子力学の方程式であるDirac方程式は，次の式で与えられます．

ここで，

です．γは4×4の行列でガンマ行列といい，σは2×2の行列でPauli行列です．また，mは質量です．
　対応するLagrangian密度は，

です．ただし，Minkowski共役な場，

を導入しました．このLagrangian密度をEuler-Lagrange方程式，

に代入すると，確かにDirac方程式が導出されることを確認しておきましょう．Euler-Lagrange方程式のφは，この場合，に置き換えます．まず，第１項は，

となります．次に，第２項は，

となります．したがって，Euler-Lagrange方程式は，

となります．確かに，Dirac方程式が導かれました．
　Hamiltonian密度も求めておきましょう．一般化運動量πは，

ここで，

となるので，

となります．したがって，Hamiltonian密度は，

（Dirac方程式より，）

と導かれます．

3.2 Dirac場の正準量子化

量子論ではオブザーバブルは演算子で表されることになります．Dirac場ψを演算子に格上げした瞬間に，場の量子化が実行されたことになります．この際，演算子は積の順序が問題となりますので，交換関係を設定することになります．このような交換関係による量子化のことを正準量子化といいます．ただし，Dirac場が記述するのはFermionなので反交換関係を設定しなければなりません．Dirac場ψとその一般化運動量πの間に次の同時刻反交換関係を設定します．

ただし，反交換子は，

で定義されます．演算子を表すハットは省略しました．また，場の量ψやπは連続量なので，δ関数を使って反交換関係を表しています．
　次に，場ψをFourier変換します．

σは電子のスピンの自由度を表します．また，単にxやkと書いているのは，

を意味します．したがって，kxの表記で，

を表します．また，ωとの間には，特殊相対性理論の要請より，

の関係が成立します．これを，On-shell条件といいます．このとき，

となります．Minkowski共役な場は，

となります．ここで，展開係数はエルミート演算子で，次の反交換関係が成立します．

反交換関係(3)式が成立することを確認するために，場φをFourier変換した(2)式をもとの同時刻反交換関係(1)式の左辺に代入して，(3)式を使って(1)式が成立することを確かめます．

（に加え，より，も成立します．）

（柏太郎著”演習場の量子論”サイエンス社
p41 (2.94)(2.95)式より）

（の１次元の式より，３次元にして，
が成立します．）

同様にして，(1)式の残りの２式も確かめることができます．
　Hamiltonianを展開係数で表してみましょう．Hamiltonianは，

です．ここで，

において，エルミート共役をとると，

となります．上のHamiltonianに代入して計算します．

　

　

　

　

（の１次元の式より，３次元にして，
が成立します．）

　

（に加え，より，が成立します．）

　

（柏太郎著”演習場の量子論”サイエンス社
p41 (2.91)(2.92)式より）

　

　

　

ここで，第３項はデルタ関数の性質

より，のときのωの値が出てくることになります．

これは定数なので，エネルギー軸の原点をずらして0にすることができます．したがって，Hamiltonianは，

で与えられることになります．