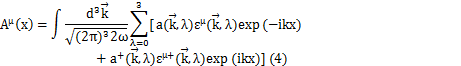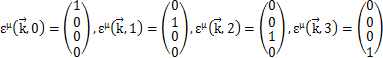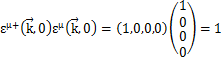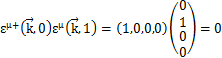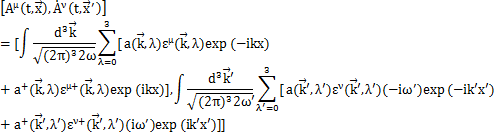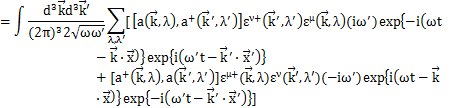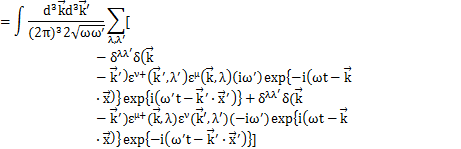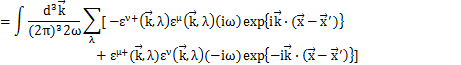4.1 Maxwell場の古典論

特殊相対論的電磁気学の方程式であるMaxwell方程式は，次の式で与えられます．

ここで，

です．対応するLagrangian密度は，

で与えられます．このLagrangian密度をEuler-Lagrange方程式，

に代入すると，確かにMaxwell方程式が導出されることを確認しておきましょう．Euler-Lagrange方程式のφは，この場合，に置き換えます．

ここで，

ですが，最後の式の第２項で添え字のμ，νを入れ換えると，の反対称性より，

となります．したがって，

なので，与えたLagrangian密度は，

と書き直すことができます．このLagrangian密度の第１項は，

とも書き直すことができることにも注意しましょう．このとき，Euler-Lagrange方程式，

は，

より，

となります．確かに，Maxwell方程式が導かれました．
　次に，Sourceが無く，の場合を考えます．このとき，Lagrangian密度は，

となり，真空中のMaxwell方程式は，

となります．
　(1)式のLagrangian密度はゲージ不変性をもっていますが，ゲージを固定するため，αを任意定数として，

というゲージ固定項を手で加えます．このとき，Lagrangian密度は，

と，修正されます．ここで，α=1というFeynmanゲージを選ぶと，

となります．この(2)式のLagrangian密度について，一般化運動量を計算します．ここで，前述の式変形と同様に，

と書き直すことができます．さらに，この式の右辺第１項は，前述の式変形と同様に，

とも書き直すことができることにも注意しましょう．また，右辺第２項を，

と変形しておきます．したがって，一般化運動量の時間成分は，

となります．空間成分は，

となります．

4.2 Maxwell場の正準量子化

量子論ではオブザーバブルは演算子で表されることになります．Maxwell場を演算子に格上げした瞬間に，場の量子化が実行されたことになります．この際，演算子は積の順序が問題となりますので，交換関係を設定することになります．このような交換関係による量子化のことを正準量子化といいます．次の同時刻交換関係を設定します．

演算子を表すハットは省略しました．また，場の量やは連続量なので，δ関数を使って交換関係を表しています．次に，場をFourier変換します．

単にxやkと書いているのは，

を意味します．したがって，kxの表記で，

を表します．また，ωとの間には，特殊相対性理論の要請より，

の関係が成立します．これを，On-shell条件といいます．このとき，

となります．また，εは偏光ベクトルといい，４次元ミンコフスキー時空における基本単位ベクトル（基底ベクトル）です．εは，お互いに独立ならば自由に選択することができますが，簡単のため，の向きがz方向になるように基準系を設定して，

とします．このとき，光はz方向に進んでいるとしたので，

が成立します．すなわち，λ=1,2は横波成分を表します．そして，λ=3は縦波成分を，λ=0は時間成分を表します．上の具体的表式より，

が成立します．例えば，

等です．つまり，εは規格直交系を形成していることがわかります．さらに，

が成立します．具体的表式より，例えば，

等です．上式はεの完全性を表しています．展開係数に目を向けましょう．これらはエルミート演算子で，次の交換関係が成立します．

交換関係(5)式が成立することを確認するために，場をFourier変換した(4)式をもとの同時刻交換関係(3)式の左辺に代入して，(5)式を使って(3)式が成立することを確かめます．以下，(3)式の第１式を計算します．

（に加え，より，も成立します．）

（の１次元の式より，３次元にして，
が成立します．さらに前述の，
を利用します．）

確かに，(3)式の第１式が導かれました．第２式，第３式も同様に導くことができます．