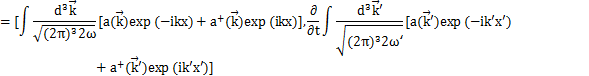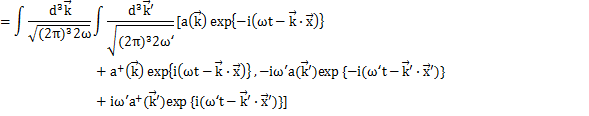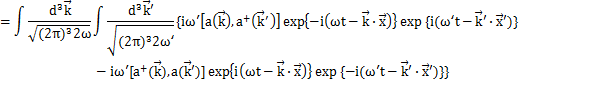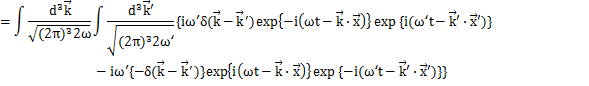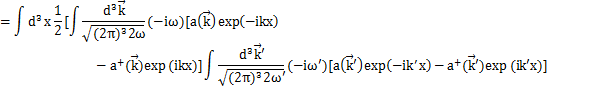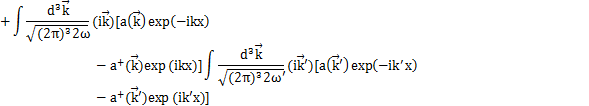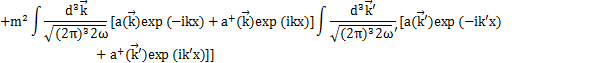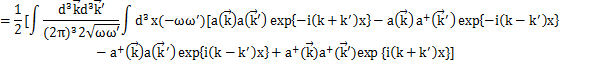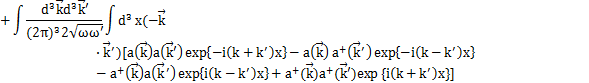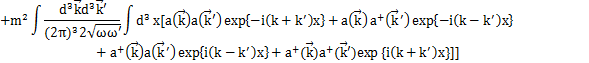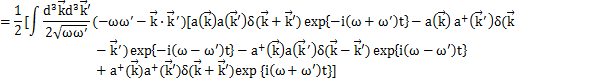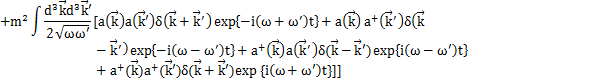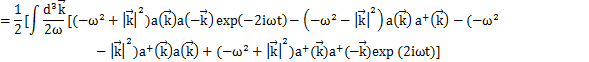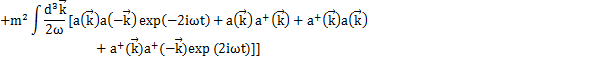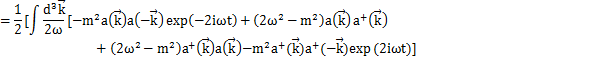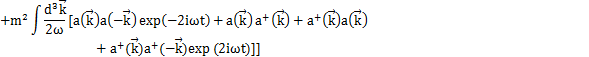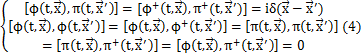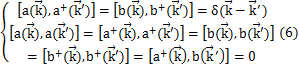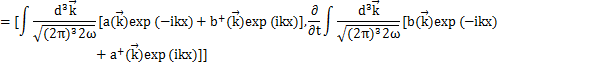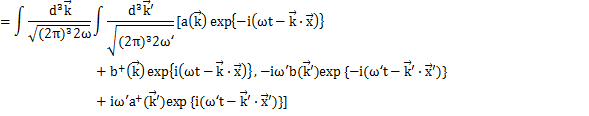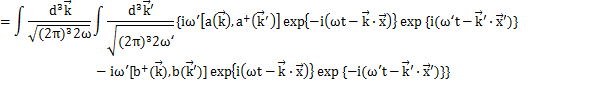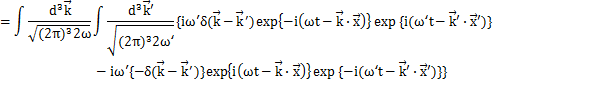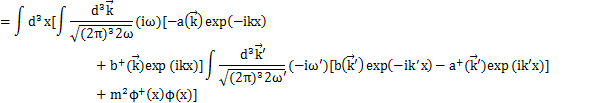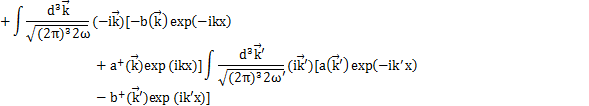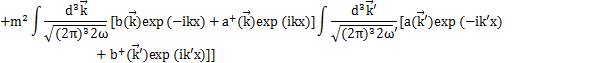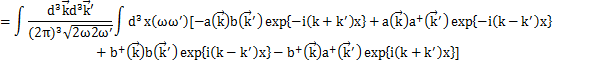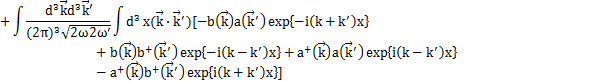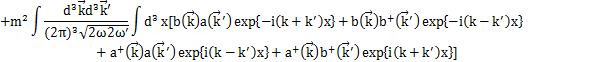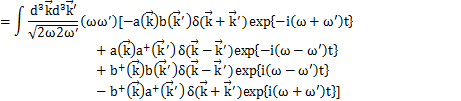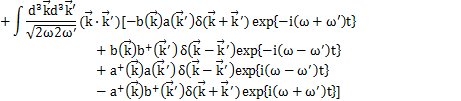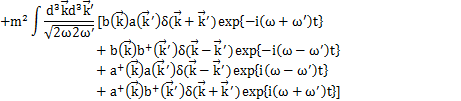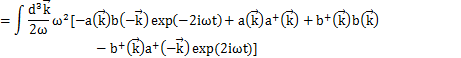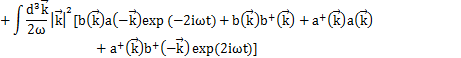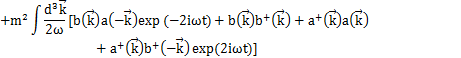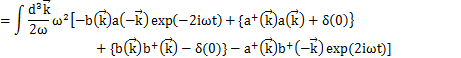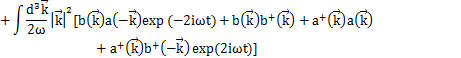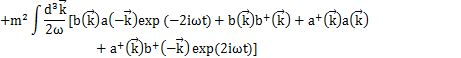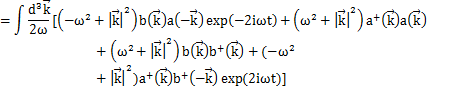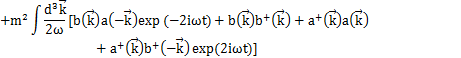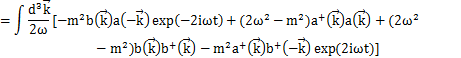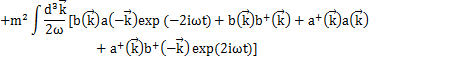2.1 実Klein-Gordon場の古典論

特殊相対論的量子力学の方程式であるKlein-Gordon方程式は，次の式で与えられます．

ここで，

であり，mは質量です．また，φ(x)は一成分のみの波動場で，ローレンツ変換，

について，

と変換されるとすれば，ローレンツ変換の下でKlein-Gordon方程式は，

となります．ここで，はローレンツ不変量であり，

が成立するので，

となります．は，と全く同形の方程式を満たすことが要求されるので，φのローレンツ変換性は，

となります．この変換性はスカラーなので，φはスカラー場とも呼ばれます．
　φ(x)が実数の場合，つまり実Klein-Gordon場の場合，対応するLagrangian密度は，

となります．このLagrangian密度をEuler-Lagrange方程式，

に代入すると，確かにKlein-Gordon方程式が導出されることを確認しておきましょう．まず，第１項は，

となります．第２項を計算するため，Lagrangian密度を，

と変形しておきます．μやνをρやσに置き換えても，Einsteinの規約によりそれぞれ和をとることになりますので，問題ありません．このとき，

となります．１行目から２行目への変形にはを使いました．２行目から３行目への変形は，によって，添え字を上に上げたのですね．したがって，Euler-Lagrange方程式は，

となります．確かに，Klein-Gordon方程式が導かれました．
　Hamiltonian密度も求めておきましょう．一般化運動量πは，

となります．したがって，Hamiltonian密度は，

と導かれます．

2.2 複素Klein-Gordon場の古典論

Klein-Gordon場φ(x)が複素数の場合，つまり複素Klein-Gordon場の場合は，独立な場はとこれにエルミート共役な関係にある場の２種類となり，それぞれKlein-Gordon方程式を満たします．このとき，Lagrangian密度は，

になります．確かに，このLagrangian密度からEuler-Lagrange方程式により，複素Klein-Gordon方程式が導出されることを確認しましょう．

の第１項は，

となります．また，

となります．このとき，Euler-Lagrange方程式は，

となり，エルミート共役をとったKlein-Gordon方程式が導かれます．次にエルミート共役をとっていないφ(x)についての関係を導くには，このエルミート共役をとったKlein-Gordon方程式について，さらに両辺エルミート共役をとります．このとき，

が成立します．以上で，複素Klein-Gordon方程式が計２式導かれました．
　Hamiltonian密度も求めておきましょう．まず，に共役な一般化運動量は，

となります．したがって，Hamiltonian密度は，

となります．

2.3 実Klein-Gordon場の正準量子化

量子論ではオブザーバブルは演算子で表されることになります．実Klein-Gordon場φを演算子に格上げした瞬間に，場の量子化が実行されたことになります．この際，演算子は積の順序が問題となりますので，交換関係を設定することになります．このような交換関係による量子化のことを正準量子化といいます．量子力学での位置演算子と運動量演算子の間の交換関係，

を参考にして，実Klein-Gordon場φとその一般化運動量πの間に次の同時刻交換関係を設定します．

演算子を表すハットは省略しました．また，場の量φやπは連続量なので，δ関数を使って交換関係を表しています．
　次に，場φをFourier変換します．

単にxやkと書いているのは，

を意味します．したがって，kxの表記で，

を表します．また，ωとの間には，特殊相対性理論の要請より，

の関係が成立します．これを，On-shell条件といいます．このとき，

となります．場φをFourier変換した式には，第２項が付いています．これは，φが実の場，つまり，エルミートの場であることを満たすために付け加えられたものです．確かに，(2)式より，

となります．ここで，展開係数はエルミート演算子で，次の交換関係が成立します．

交換関係(3)式が成立することを確認するために，場φをFourier変換した(2)式をもとの同時刻交換関係(1)式の左辺に代入して，(3)式を使って(1)式が成立することを確かめます．

　

　

　

　

（に加え，より，も成立します．）

　

（の１次元の式より，３次元にして，
が成立します．）

　

　

同様にして，(1)式の残りの２式も確かめることができます．
　Hamiltonianを展開係数で表してみましょう．Hamiltonianは，

です．ここで，

でしたが，

より，

となります．上のHamiltonianに代入して計算します．

　

　

（の１次元の式より，３次元にして，
が成立します．）

　

（に加え，より，が成立します．）

　

　

　

　

　

ここで，第２項はデルタ関数の性質

より，のときのωの値が出てくることになります．

これは定数なので，エネルギー軸の原点をずらして0にすることができます．したがって，Hamiltonianは，

で与えられることになります．

2.4 複素Klein-Gordon場の正準量子化

実Klein-Gordon場の場合と同様に，複素Klein-Gordon場φとその一般化運動量πの間に次の同時刻交換関係を設定し量子化します．ただし，との関係がありました．

演算子を表すハットは省略しています．また，場の量φやπは連続量なので，δ関数を使って交換関係を表しています．
　次に，場φをFourier変換します．

この式のエルミート共役をとると，

です．演算子bが導入されましたので，φは実の場ではないことがわかります．ここで，展開係数はエルミート演算子で，次の交換関係が成立します．

交換関係(6)式が成立することを確認するために，場φをFourier変換した(5)式をもとの同時刻交換関係(4)式の左辺に代入して，(6)式を使って(5)式が成立することを確かめます．

最後の式は，前Sectionの実Klein-Gordon場の交換関係についての途中の計算式と全く同じです．したがって，以下，同じ計算により，

が導出されます．同様にして，(4)式の残りの全ての式も確かめることができます．
　Hamiltonianを展開係数で表してみましょう．Hamiltonianは，

です．ここで，

でしたが，

より，

となります．上のHamiltonianに代入して計算します．

　

　

（の１次元の式より，３次元にして，
が成立します．）

　

（に加え，より，が成立します．）

　

　

　

　

　

　

最後の定数項は，前Sectionのときと同様にして，0にすることができます．したがって，Hamiltonianは，

となります．