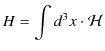Part1 古典場と自由量子場
Chapter1 場の古典論
1.1 自然単位系と特殊相対論的Notation
素粒子論で使用する単位系は,
とする自然単位系を採用します.言うまでもなく,![]() はプランク定数を
はプランク定数を ![]() で割ったもの,
で割ったもの,![]() は光速です.
は光速です.
場の量子論は,特殊相対性理論と量子力学を融合し,場という概念を推し進めた理論ですが,ここで,特殊相対性理論の表記についてまとめておきます.まず,計量テンソルは,
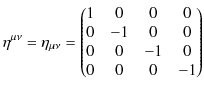
とします.また,ギリシア文字は
![]() のようにとります.第0成分は時間成分,第1,2,3成分は空間成分です.座標ベクトルは,反変ベクトルが,
のようにとります.第0成分は時間成分,第1,2,3成分は空間成分です.座標ベクトルは,反変ベクトルが,
であり,共変ベクトルが,
です.4元ベクトルとしては,
や,
も挙げられます.2式とも最後の式変形には,![]() としたアインシュタイン-ド・ブロイの関係式を使っています.また,上下に同じギリシア文字が対になって現れる場合,0,1,2,3について和をとるというアインシュタインの規約を使います.アインシュタインの規約を使って,インターバルの2乗は,
としたアインシュタイン-ド・ブロイの関係式を使っています.また,上下に同じギリシア文字が対になって現れる場合,0,1,2,3について和をとるというアインシュタインの規約を使います.アインシュタインの規約を使って,インターバルの2乗は,
と定義されます.ローレンツ変換,
のもとで,インターバルの2乗は,
と変換しますが,インターバルの2乗はスカラー,すなわちローレンツ不変量なので,
ですから,
すなわち,
が成立します.最後の式を満たす変換をローレンツ変換と定義することができます.縮約をとったスカラー,すなわちローレンツ不変量の例としては,インターバルの2乗の他に,
や,
等があります.また,微分演算子として,
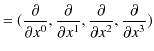 |
||
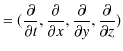 |
||
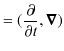 |
と,
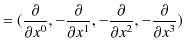 |
||
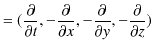 |
||
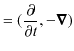 |
があります.縮約をとると,
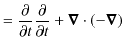 |
||
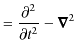 |
となります.
1.2 Lagrangian形式
場という量を一般的に,
と表しておきます.ここで,![]() は時間1次元と空間3次元をまとめて表しています.
は時間1次元と空間3次元をまとめて表しています.
つまり,場という量は空間の関数になっていて,それが時間的に変動するものであると考えることができます.
場をLagrangian形式の解析力学で取り扱ってみましょう.まず,今後よく使う積分の表記方法を定義しておきます.空間3次元の積分として,
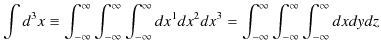
を使います.積分範囲が ![]() から
から ![]() になっているのは,量子力学の場合と同様に,一般に量子は全空間に存在する確率があるためです.(このChapterは古典論についてですが,後のChapterを考慮して,このように定義しておきます.)4次元時空の積分は,
になっているのは,量子力学の場合と同様に,一般に量子は全空間に存在する確率があるためです.(このChapterは古典論についてですが,後のChapterを考慮して,このように定義しておきます.)4次元時空の積分は,
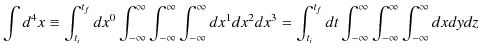
とします.ここで,時間は ![]() から始まり,
から始まり,![]() で終わるとしています.Lagrangian
で終わるとしています.Lagrangian ![]() をLagrangian密度
をLagrangian密度
![]() で表す場合,空間3次元について積分して,
で表す場合,空間3次元について積分して,
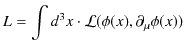
となります.さらに,Lagrangian ![]() を時間で積分した量を作用
を時間で積分した量を作用 ![]() といいます.
といいます.
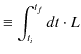 |
||
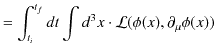 |
||
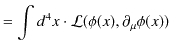 |
ここで,ある領域 ![]() に対して,場
に対して,場 ![]() を,
を,
となるように変化させます.(量子論では領域の空間部分は全空間になります.この場合も,以下の議論はそのまま成立します.)ただし,領域の境界で,
が成立するものとします.場 ![]() が上述のように変わるとき,作用
が上述のように変わるとき,作用 ![]() は,
は,
と表記されますが,
となることを自然は要求します.言い直すと,作用 ![]() を最小にするように自然はできているのです.この原理を最小作用の原理と言います.左辺を次のように計算します.
を最小にするように自然はできているのです.この原理を最小作用の原理と言います.左辺を次のように計算します.
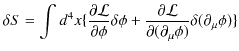
ここで,
ですから,
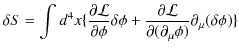
となります.この式の右辺第2項は,
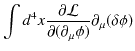 |
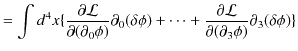 |
|
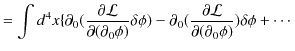 |
||
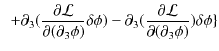 |
||
![$\displaystyle =\int dx^{1}dx^{2}dx^{3}[\dfrac{\partial\mathcal{L}}{\partial(\partial_{0}\phi)}\delta\phi]_{Boundary}+\cdots$](ja_Chapter1_ClassicalFieldTheory_images/img90.png) |
||
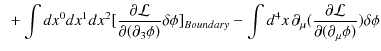 |
||
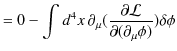 |
となります.最後の変形には境界面おいて,
であることを使いました.よって,
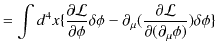 |
||
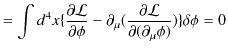 |
となります.任意の
![]() について,この式が成立するためには,被積分が 0 にならなければなりません.故に,
について,この式が成立するためには,被積分が 0 にならなければなりません.故に,
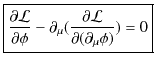 |
(1.1) |
が成立します.この場の方程式をEuler-Lagrange方程式と言います.
Hamiltonianについても見ておきましょう.通常の解析力学を場について拡張した議論を行います.まず,場の共役運動量密度 ![]() を,
を,
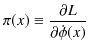
で定義します.更に,Hamiltonian密度
![]() を定義します.
を定義します.
このHamiltonian密度
![]() から,Hamiltonian
から,Hamiltonian ![]() が計算されます.
が計算されます.