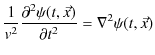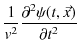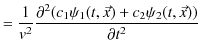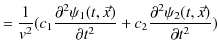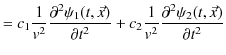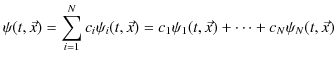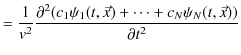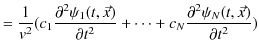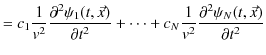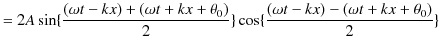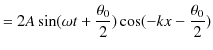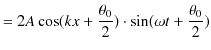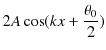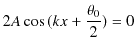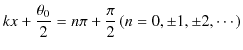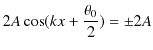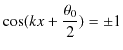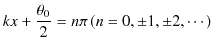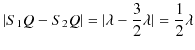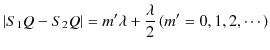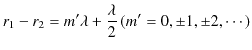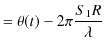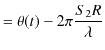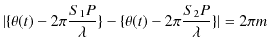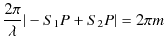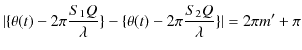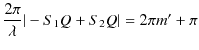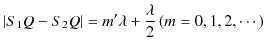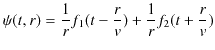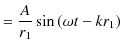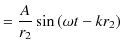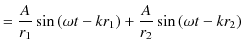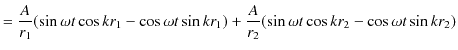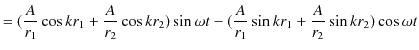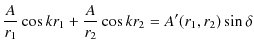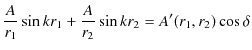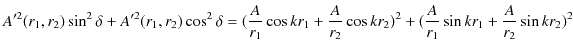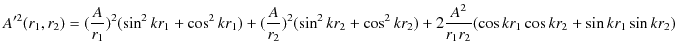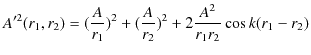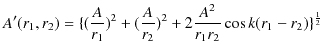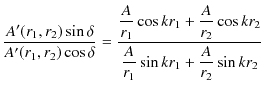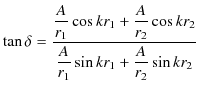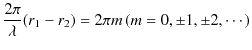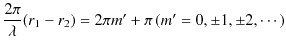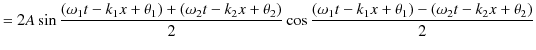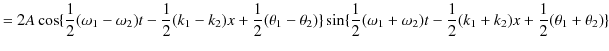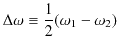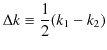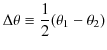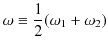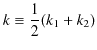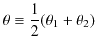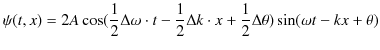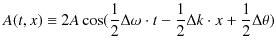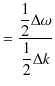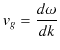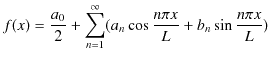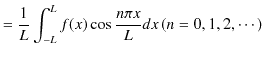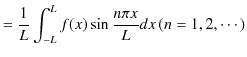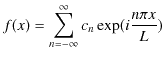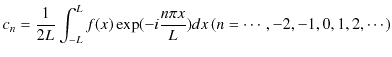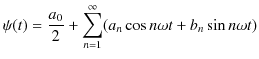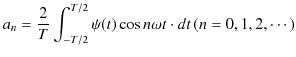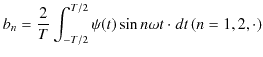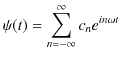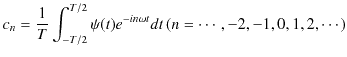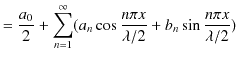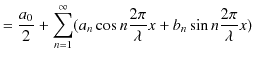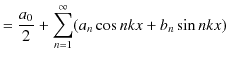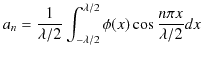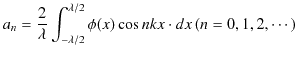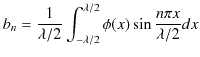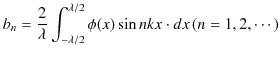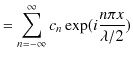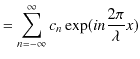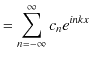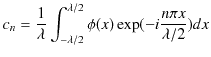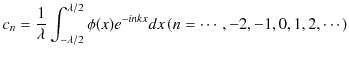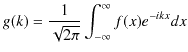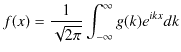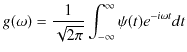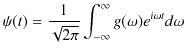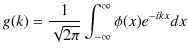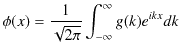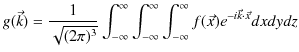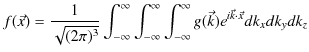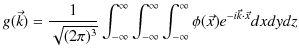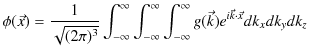Chapter6 干渉と回折
6.1 重ね合わせの原理
2つの波動が衝突する場合,どのような現象が起こるのでしょうか? 実際にウェーブマシンという波動を作る簡単な装置を使って試してみると,図のような結果になることが確かめられます.図の青色で示されている2つのパルス波を衝突させるのですが,それぞれの変位を
 と
と
 とします.緑色で示されている波動が,衝突した際にできる波形であり,合成波といいます.そして,その変位を
とします.緑色で示されている波動が,衝突した際にできる波形であり,合成波といいます.そして,その変位を 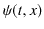 と表します.
と表します.
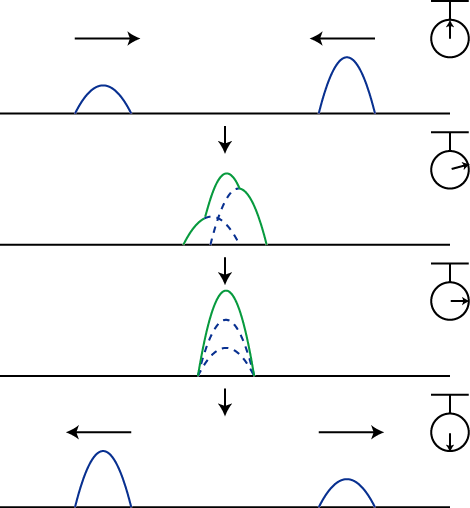
Figure6.1: 重ね合わせの原理
このとき,
という関係が成立することが観測されます.この関係を重ね合わせの原理といいます.また,衝突した後は,元の波動が何事もなかったかのように素通りしていくことが観測されます.このことを波動の独立性といいます.以上の重ね合わせの原理および波動の独立性は,ウェーブマシンを使った初等的な実験事実であると理解できます.
重ね合わせの原理に関して,前のChapterの3次元波動方程式,
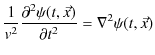 |
(6.1) |
を使って議論を深めていきましょう.ここで,3次元波動方程式において,
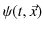 は変位だけに留まらず,波動一般量を表すものであったことに注意します.重ね合わせの原理は変位だけでなく,波動が運ぶ一般量について成立することを併せて議論するのです.実際に行うことは,
は変位だけに留まらず,波動一般量を表すものであったことに注意します.重ね合わせの原理は変位だけでなく,波動が運ぶ一般量について成立することを併せて議論するのです.実際に行うことは,
が,(6.1)式のそれぞれの解であるとき,
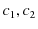 を実定数であるとして,
を実定数であるとして,
が,やはり解であることを証明するのです.このことは(6.1)式の微分方程式の線形性を利用して,次のように実行できます.
(証明終.)さらに,波動の数を 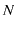 個にして,各波動一般量に実定数を掛けた量についても同様な関係が成立することが,次のように数学的に証明されます.つまり,
個にして,各波動一般量に実定数を掛けた量についても同様な関係が成立することが,次のように数学的に証明されます.つまり,
が,(6.1)式のそれぞれの解であるとき,
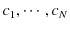 を実定数であるとして,
を実定数であるとして,
も,やはり解であることが,次のように示されます.
(証明終.)次の拡張した重ね合わせの原理が成立することが確かめられました.すなわち,
原理6.1(重ね合わせの原理) "複数の波動一般量が波動方程式を満たすとき,それらの波動一般量に実定数をかけて加え合わせた量も,波動方程式の解になります."
が成り立ちます.以下のSectionで,重ね合わせの原理を使って説明される波動独特の現象に関して,見ていくことにしましょう.(主に,2つの波動についての狭義の重ね合わせの原理を使っていくことになります.)
6.4 回折
波動の進路にその波動を伝えない障害物による隙間がある場合,その障害物の背後に波動が回り込む現象を回折といいます.回折は隙間や障害物の幅に対して波長が小さいとき顕著には起こりませんが,同程度以上になると目立つようになります.
6.5 波束
振幅が同じで,波数,角振動数が少し違う,同じ向きに進む1次元の2つの正弦波があるときに起こる現象について考えましょう.2つの正弦波は次式で表されます.
重ね合わせの原理により,合成波の波動一般量 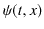 は次のようになります.
は次のようになります.
ここで,
と,
とおくと,
となります.このとき,
という因子は,
と比較して,![$ t[s],x[m]$](ja_Chapter6_InterferenceAndDiffraction_images/img155.png) に対する変化の割合が緩やかですから,ある瞬間に空間的な波動の形を表すと図のようになります.
に対する変化の割合が緩やかですから,ある瞬間に空間的な波動の形を表すと図のようになります.
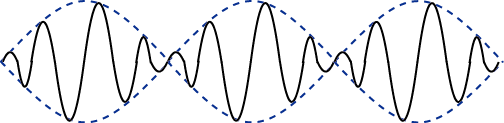
Figure6.4: 波束
正弦波 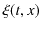 の振幅が
の振幅が 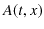 のように変化しているように見えます.(図で
のように変化しているように見えます.(図で 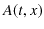 は青い破線で表されています.)このような波動のかたまりを波束といいます.一般に,正弦波の速さは,
は青い破線で表されています.)このような波動のかたまりを波束といいます.一般に,正弦波の速さは,
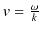 なので,波束の速さ(これを群速度といいます.)
なので,波束の速さ(これを群速度といいます.)
![$ v_{g}[m/s]$](ja_Chapter6_InterferenceAndDiffraction_images/img160.png) は,
は,
です.ここで無限小の極限をとると,群速度は,
となります.群速度に対して,波面の速度
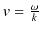 を位相速度といいます.
を位相速度といいます.
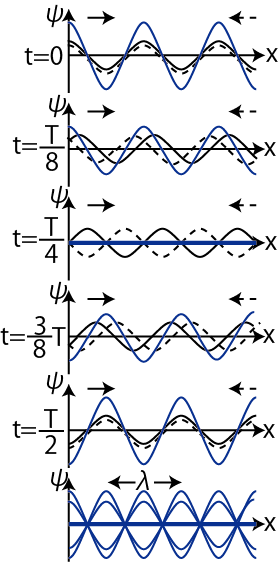
![]() 毎の様子を示しました.この図からわかるように,合成波は右にも左にも進みません.このように,振動するが進まない波動を定常波といいます.それに対して,もとの波動のように進む波を進行波といいます.定常波において,最も振動する点を腹,全く振動しない点を節といいます.また,図のように定常波の腹2つ分で波長
毎の様子を示しました.この図からわかるように,合成波は右にも左にも進みません.このように,振動するが進まない波動を定常波といいます.それに対して,もとの波動のように進む波を進行波といいます.定常波において,最も振動する点を腹,全く振動しない点を節といいます.また,図のように定常波の腹2つ分で波長
![]() を定義すると,それはもとの進行波の波長に等しくなります.さらに,図を見るとわかるように,媒質が1振動するのに要する時間(定常波の周期)は,もとの進行波の周期に等しくなっています.
を定義すると,それはもとの進行波の波長に等しくなります.さらに,図を見るとわかるように,媒質が1振動するのに要する時間(定常波の周期)は,もとの進行波の周期に等しくなっています.![]() 軸上をお互いに逆向きに進む2つの正弦波を,
軸上をお互いに逆向きに進む2つの正弦波を,