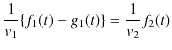Chapter7 反射・透過・屈折
7.1 1次元波動の反射と透過
簡単のため,1次元の場合を考えます.媒質が途中で途切れているとき,その端で波動は反射します.1本の弦の振動や,ウェーブマシンという簡単な実験装置を想定すると考えやすいでしょう.このときの反射には,端に力が働かず自由に動ける自由端の場合と,端が固定されている固定端の場合の2通りがあります.以下,順番に見ていくことにします.
まず,自由端反射について調べてみましょう.弦やウェーブマシンに沿って,![]() 軸をとり,自由端を原点にして,変位を
軸をとり,自由端を原点にして,変位を ![]() とします.張力
とします.張力 ![]() の
の ![]() 方向の力の成分は,張力と水平成分のなす角を
方向の力の成分は,張力と水平成分のなす角を
![]() として,
として,
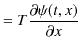 |
となります.原点にある自由端における境界条件は,![]() 方向に力が働かないので,
方向に力が働かないので,
と表せます.この条件をノイマン境界条件といいます.ここで,![]() を波動一般量に拡張し,逆にノイマン境界条件(7.1)式が成立するときの反射を自由端反射と定義します.
を波動一般量に拡張し,逆にノイマン境界条件(7.1)式が成立するときの反射を自由端反射と定義します.![]() の方から,自由端に向かって正の向きに進む波動(入射波),
の方から,自由端に向かって正の向きに進む波動(入射波),
が来たときを考えます.波動が自由端に達したとき,負の向きに進む反射波,
が生じます.波動は重ね合わされて,
という波動一般量になります.ここで,
とおきます.このとき,ノイマン境界条件(7.1)より,
![$\displaystyle [\dfrac{\partial\psi(t,x)}{\partial x}]_{x=0}=-\dfrac{1}{v}[\dfra...
...ial\xi}]_{x=0}+\dfrac{1}{v}[\dfrac{\partial g_{1}(\eta)}{\partial\eta}]_{x=0}=0$](ja_Chapter7_Reflection_Transmission_Refraction_images/img17.png) |
||
![$\displaystyle [\dfrac{\partial f_{1}(\xi)}{\partial\xi}]_{x=0}=[\dfrac{\partial g_{1}(\eta)}{\partial\eta}]_{x=0}$](ja_Chapter7_Reflection_Transmission_Refraction_images/img19.png) |
となりますが,![]() のとき,
のとき,
![]() となるので,
となるので,
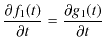 |
||
となります.ここで,
![]() のときには,反射波もないので,
のときには,反射波もないので,
![]() になるので,
になるので,![]() です.したがって,
です.したがって,
となります.ここで,変数 ![]() を変数
を変数 ![]() に置き換えて,
に置き換えて,
とします.このとき,反射波は,
です.つまり,入射波と反射波の関係は,
となります.反射波を求めるには,媒質が ![]() まで続いているとみなし入射波を延長して,その入射波の延長をそのまま縦軸に関して折り返せばよいのです.連続した正弦波を送り続けた場合を図示します.
まで続いているとみなし入射波を延長して,その入射波の延長をそのまま縦軸に関して折り返せばよいのです.連続した正弦波を送り続けた場合を図示します.
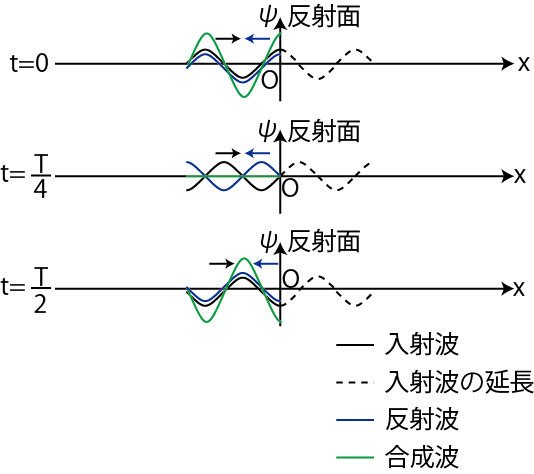
Figure7.1: 自由端反射
この場合,入射波と反射波は振幅・波長・周期が等しく反対向きに進んでいるので,合成波は定常波になります.また,自由端そのものは定常波の腹になります.
次に,固定端反射について調べてみましょう.固定端を原点にとり,変位
![]() について境界条件を表すと次のようになります.
について境界条件を表すと次のようになります.
この(7.2)式の条件をディリクレ境界条件といいます.ここで,![]() を波動一般量に拡張し,逆に波動一般量
を波動一般量に拡張し,逆に波動一般量 ![]() についてディリクレ境界条件(7.2)式が成立するときの反射を固定端反射と定義します.
についてディリクレ境界条件(7.2)式が成立するときの反射を固定端反射と定義します.![]() の方から,固定端に向かって正の向きに進む波動(入射波),
の方から,固定端に向かって正の向きに進む波動(入射波),
が来たときを考えます.波動が固定端に達したとき,負の向きに進む反射波,
が生じます.波動は重ね合わされて,
の波動一般量になります.ディリクレ境界条件(7.2)式より,
となります.ここで,変数 ![]() を変数
を変数 ![]() に置き換えて,
に置き換えて,
となります.故に,反射波は,
となります.つまり,入射波と反射波の関係は,
です.反射波を求めるためには,媒質が ![]() まで続いているとみなし,入射波を延長して,その入射波の延長の波動一般量を反転し,縦軸に関して折り返せばよいです.連続した正弦波を送り続けた場合を図示します.
まで続いているとみなし,入射波を延長して,その入射波の延長の波動一般量を反転し,縦軸に関して折り返せばよいです.連続した正弦波を送り続けた場合を図示します.
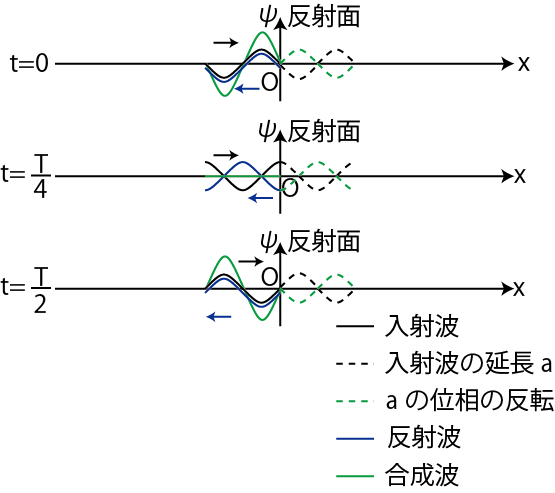
Figure7.2: 固定端反射
この場合,入射波と反射波は振幅・波長・周期が等しく反対向きに進んでいるので,合成波は定常波になります.また,固定端そのものは定常波の節になります.
波動の反射は媒質の端だけでなく,2つの異なる媒質が接続されている場合にも起こります.このとき,反射だけでなく,透過という現象も起こっています.ここでも1次元の場合を考えます.![]() の方から,境界面に向かって正の向きに進む波動(入射波),
の方から,境界面に向かって正の向きに進む波動(入射波),
が来たときを考えます.波動が境界面に達したとき,負の向きに進む反射波,
と,![]() の領域を正の向きに進む波動(透過波),
の領域を正の向きに進む波動(透過波),
が生じます.ただし,![]() の媒質を媒質1,そのときの波動の速さを
の媒質を媒質1,そのときの波動の速さを
![]() とし,
とし,![]() の媒質を媒質2,そのときの波動の速さを
の媒質を媒質2,そのときの波動の速さを
![]() としました.ここで,
としました.ここで,![]() は媒質1と媒質2の波動について等しくならなければなりません.しががって,境界条件,
は媒質1と媒質2の波動について等しくならなければなりません.しががって,境界条件,
が成立します.また,張力の ![]() 方向への成分は,媒質1と媒質2で等しくならなければなりません.したがって,境界条件,
方向への成分は,媒質1と媒質2で等しくならなければなりません.したがって,境界条件,
![$\displaystyle [\dfrac{\partial\psi_{i}(t,x)}{\partial x}]_{x=0}+[\dfrac{\partia...
..._{r}(t,x)}{\partial x}]_{x=0}=[\dfrac{\partial\psi_{t}(t,x)}{\partial x}]_{x=0}$](ja_Chapter7_Reflection_Transmission_Refraction_images/img53.png)
が成立します.これらを次のように書き直します.
となります.ここで,変数
![]() を,
を,
と定義すると,(7.4)式は,
![$\displaystyle -\dfrac{1}{v_{1}}[\dfrac{\partial f_{1}(\xi_{1})}{\partial\xi_{1}...
...{x=0}=-\dfrac{1}{v}_{2}[\dfrac{\partial f_{2}(\xi_{2})}{\partial\xi_{2}}]_{x=0}$](ja_Chapter7_Reflection_Transmission_Refraction_images/img63.png)
となります.![]() では,
では,
なので,
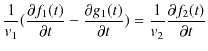 |
||
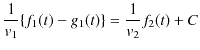 |
となりますが,
![]() のときは,
のときは,
![]() となるので,積分定数
となるので,積分定数 ![]() は 0 になります.故に,
は 0 になります.故に,
となります.(7.3)式
![]() (7.5)式より,
(7.5)式より,
となります.(7.3)式
![]() (7.5)式より,
(7.5)式より,
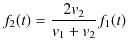 |
となります.したがって,変数 ![]() を
を
![]() あるいは
あるいは
![]() と置き換えて,反射波と透過波は,それぞれ次のように表されます.
と置き換えて,反射波と透過波は,それぞれ次のように表されます.
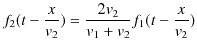 |
これらの式から,反射波・透過波はそれぞれ入射波と同じ波形をもつことがわかります.反射波は
![]() と
と
![]() の大小関係により,同位相のときと逆位相のときがありますが,透過波は常に入射波と同位相になります.
の大小関係により,同位相のときと逆位相のときがありますが,透過波は常に入射波と同位相になります.
7.2 3次元波動の反射と屈折
3次元波動の反射・屈折を考えます.媒質の境界面は平面で,そこに正弦波の平面波が入射する場合を取り扱います.入射波,反射波,屈折波の波動一般量をそれぞれ次のように表します.
ここで,![]() は波数ベクトルで,向きは平面波の進行方向を示します.また,媒質の境界面が
は波数ベクトルで,向きは平面波の進行方向を示します.また,媒質の境界面が ![]() 面になるように,かつ入射波の進行方向を示す波数ベクトルが
面になるように,かつ入射波の進行方向を示す波数ベクトルが ![]() 平面にあるように座標をとっておきます.状況を図示しておきます.
平面にあるように座標をとっておきます.状況を図示しておきます.
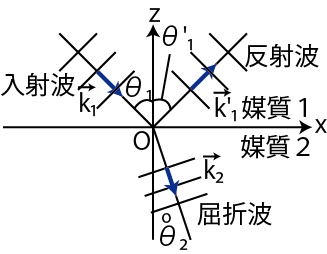
Figure7.3: 反射と屈折
波動一般量
![]() は境界面上では,どちらの媒質中の波動について考えても等しくならなければなりません.故に,境界面上では,
は境界面上では,どちらの媒質中の波動について考えても等しくならなければなりません.故に,境界面上では,
が成立しなければなりません.そのためには3つの正弦波の位相が境界面上のすべての点において,常に等しくならなければなりません.
すなわち,
が成立します.(7.6)式は ![]() が境界面上にあるとき,すなわち
が境界面上にあるとき,すなわち ![]() 平面内に含まれるときに成立する関係です.故に,
平面内に含まれるときに成立する関係です.故に,
です.また,入射波に関しては,進行方向を示す波数ベクトルが ![]() 平面にあるので,
平面にあるので,
と表されます.反射波と屈折波については,
とおけます.このとき,(7.6)式は次のようになります.
ここで,
![]() は境界面上の全ての点なので,上式が
は境界面上の全ての点なので,上式が ![]() と
と ![]() の値に依らずに成立するためには,
の値に依らずに成立するためには,
が成り立たなければなりません.(7.8)式より,反射波・屈折波の進行方向を示す波数ベクトルは ![]() 平面内にあることがわかりました.また,媒質1と媒質2における波動の速さを,
平面内にあることがわかりました.また,媒質1と媒質2における波動の速さを,
![]() とおくと,
とおくと,
の関係があるので,(7.7)式より,
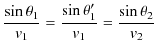 |
となります.故に,
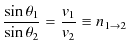 |
が成立します.それぞれの式は反射の法則,屈折の法則ですね.また,媒質1の速さ
![]() と媒質2の速さ
と媒質2の速さ
![]() の比を屈折率として定義し,
の比を屈折率として定義し,![]() と表しています.なお,境界面上で波動は連続でなければならないので,媒質1と媒質2での振動数は同じになります.
と表しています.なお,境界面上で波動は連続でなければならないので,媒質1と媒質2での振動数は同じになります.
7.3 ホイヘンスの原理
波面の進み方は,次のホイヘンスの原理によって説明されます.
"1つの波面上の全ての点は,それらを波源とする球面波(素元波)を発生させます.素元波は,波動の進む速さと等しい速さで広がり,これらの素元波が重ね合わされて,共通に接する面が次の瞬間の波面になります."
平面波と球面波が進む現象のホイヘンスの原理による説明の図を示します.
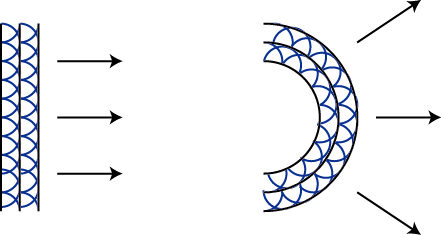
Figure7.4: ホイヘンスの原理
図の青い球面状の波が素元波です.ここで,素元波はただ単に波面の進み方を説明するための仮想的な波動なのか,あるいは実在する波動なのかという問題が生じます.これについては,次の事例を考えるとよいです.池に石を投げ込むと同心円状の球面波ができます.つまり,ある点で振動すると,必ず球面波ができるのです.平面波にしても,球面波にしても,その波面上の各点は振動しています.したがって,各点から球面波(素元波)が実際に生じているのです.そして,その素元波が重ね合わされて,新しい波面ができるのです.
ホイヘンスの原理により反射・屈折といった現象を説明しましょう.まず,反射の状況を図示します.
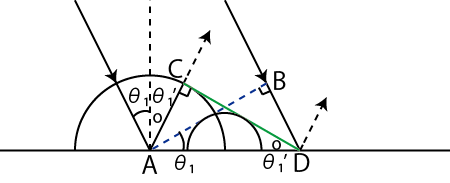
Figure7.5: 反射の法則
図の
![]() を入射角といい,
を入射角といい,
![]() を反射角といいます.線分
を反射角といいます.線分 ![]() は入射波面の中の点
は入射波面の中の点 ![]() を含む波面です.半円はホイヘンスの原理の素元波です.素元波は反射面から無数に出ていますが,その中の2つだけ描きました.素元波の共通接線の
を含む波面です.半円はホイヘンスの原理の素元波です.素元波は反射面から無数に出ていますが,その中の2つだけ描きました.素元波の共通接線の ![]() が点
が点 ![]() を通る反射波面です.ここで,三角形
を通る反射波面です.ここで,三角形 ![]() と三角形
と三角形 ![]() が合同であることを証明しましょう.波動の進行方向と波面は直交するので,
が合同であることを証明しましょう.波動の進行方向と波面は直交するので,
です.線分 ![]() は共通しているので,
は共通しているので,
また,入射波の点 ![]() が点
が点 ![]() に進む時間を
に進む時間を ![]() とすると,その
とすると,その ![]() の間に反射波の点
の間に反射波の点 ![]() は点
は点 ![]() まで進みます.故に,波動の速さを
まで進みます.故に,波動の速さを ![]() として,
として,
したがって,三角形の合同が証明されました.よって,
です.これは,反射の法則です.
次に,ホイヘンスの原理により,屈折の現象を説明します.媒質1から媒質2へ平面波が進行する状況を図示します.
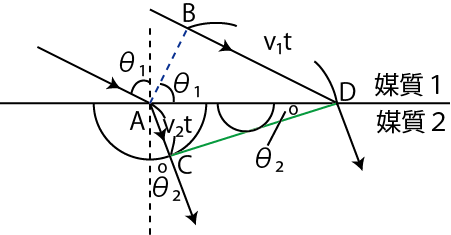
Figure7.6: 屈折の法則
図の
![]() を入射角,
を入射角,
![]() を屈折角といいます.線分
を屈折角といいます.線分 ![]() は入射波面の中の点
は入射波面の中の点 ![]() を含む波面です.半円はホイヘンスの原理の素元波です.素元波は境界面から無数に出ていますが,その中の2つだけ描きました.素元波の共通接線の
を含む波面です.半円はホイヘンスの原理の素元波です.素元波は境界面から無数に出ていますが,その中の2つだけ描きました.素元波の共通接線の ![]() が点
が点 ![]() を通る屈折波面です.入射波の点
を通る屈折波面です.入射波の点 ![]() が点
が点 ![]() に進む時間
に進む時間 ![]() の間,点
の間,点 ![]() に到着した波動は屈折波として点
に到着した波動は屈折波として点 ![]() まで進みます.波動が屈折するのは,媒質によって波動の速さが変わるためであることが理解されますね.ここで,入射角の正弦と屈折角の正弦の比を計算してみます.
まで進みます.波動が屈折するのは,媒質によって波動の速さが変わるためであることが理解されますね.ここで,入射角の正弦と屈折角の正弦の比を計算してみます.
したがって,速さの比を屈折率 ![]() として定義すると,次の屈折の法則が成立します.
として定義すると,次の屈折の法則が成立します.
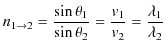
なお,境界面上で波動は連続でなければならないので,媒質1と媒質2での振動数は同じです.
![$\displaystyle [\dfrac{\partial\psi(t,x)}{\partial x}]_{x=0}=0$](ja_Chapter7_Reflection_Transmission_Refraction_images/img8.png)
![$\displaystyle [\dfrac{\partial f_{1}(t,x)}{\partial x}]_{x=0}+[\dfrac{\partial g_{1}(t,x)}{\partial x}]_{x=0}=[\dfrac{\partial f_{2}(t,x)}{\partial x}]_{x=0}$](ja_Chapter7_Reflection_Transmission_Refraction_images/img55.png)