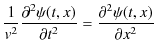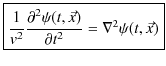Chapter5 波動方程式
5.1 正弦波
正弦波を表す式を導出します.つまり,正弦波の波動一般量の時間的,かつ空間的変化を表すことにします.まず,原点の調和振動子の振動の波動一般量
![]() は,
は,
です.ここで,![]() は振幅であり,簡単のため初期位相は
は振幅であり,簡単のため初期位相は ![]() にしました.ここで,ある時刻
にしました.ここで,ある時刻 ![]() において,原点での波動一般量
において,原点での波動一般量
![]() を図のように示しておきます.
を図のように示しておきます.
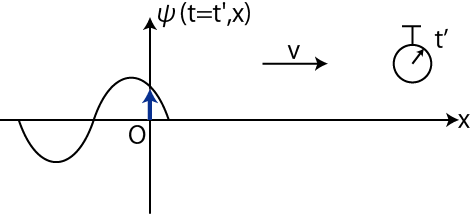
Figure5.1: 正弦波3
時間が経過し,波動が ![]() だけ進行します.そのときの時刻を
だけ進行します.そのときの時刻を ![]() とします.
とします.
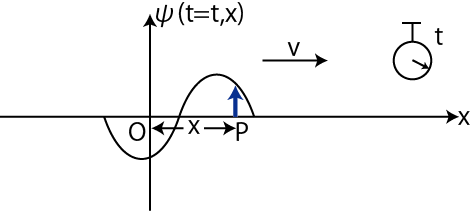
Figure5.2: 正弦波4
原点 ![]() の波動一般量が,原点から
の波動一般量が,原点から ![]() 離れた点
離れた点 ![]() に伝わるのに,時間
に伝わるのに,時間
![]() だけかかります.したがって,
だけかかります.したがって,
の関係があります.以上のことをまとめると,
"時刻 ![]() における点
における点 ![]() の波動一般量は,時刻
の波動一般量は,時刻
![]() における原点
における原点 ![]() の波動一般量に等しくなります."
の波動一般量に等しくなります."
ということになります.故に,正弦波を表す式は,
ですから,次のようになります.
ただし,![]() は次式で定義される物理量であり,波数といいます.
は次式で定義される物理量であり,波数といいます.
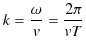 |
||
 |
つまり,波数は長さ ![]() の中に含まれる波の数になります.また,上式より,
の中に含まれる波の数になります.また,上式より,
が成立します.
正弦波を表す式には,波動一般量 ![]() に対して時間
に対して時間 ![]() と空間
と空間 ![]() の2変数が含まれます.したがって,この式を1つの図に表すことはできません.そこで,時間を止めて波動一般量
の2変数が含まれます.したがって,この式を1つの図に表すことはできません.そこで,時間を止めて波動一般量 ![]() の空間的変化を調べるか,またはある位置に着目して波動一般量
の空間的変化を調べるか,またはある位置に着目して波動一般量 ![]() の時間的変化を調べるしか方法がありません.例えば,時間を
の時間的変化を調べるしか方法がありません.例えば,時間を ![]() に固定すると,正弦波を表す式は,
に固定すると,正弦波を表す式は,
となりますが,このグラフは正弦曲線をなし,時刻 ![]() に時間を止めたときの波形を表します.一方,ある位置として原点
に時間を止めたときの波形を表します.一方,ある位置として原点 ![]() を選ぶと,正弦波を表す式は,
を選ぶと,正弦波を表す式は,
となりますが,このグラフも正弦曲線をなします.しかし,この正弦曲線は波形を表すのではないことに注意しましょう.原点という位置における波動一般量 ![]() の時間的変化,つまり,振動によって波動一般量
の時間的変化,つまり,振動によって波動一般量 ![]() が時間とともにどのように変化するかを示しています.
が時間とともにどのように変化するかを示しています.
次に,正弦波の位相について説明しておきます.正弦波は各点が調和振動子の振動をしていますが,調和振動子の運動は等速円運動の正射影の運動でした.そのとき,等速円運動の角度部分は調和振動子の位相です.したがって,正弦波の場合も各点の調和振動に各点の等速円運動が対応し,各点の位相が存在します.この各点の位相のことを正弦波の位相といいます.式の上では,正弦波を表す式の正弦の角度部分,すなわち上式では,
![]() が正弦波の位相になります.また,位相の意味を考えて,それを図示します.
が正弦波の位相になります.また,位相の意味を考えて,それを図示します.
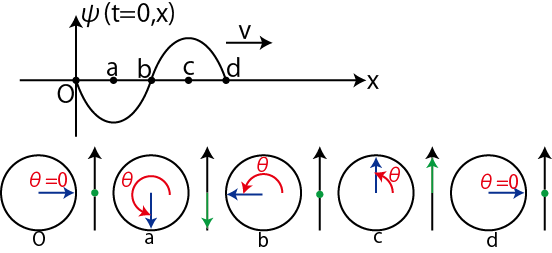
Figure5.3: 位相
図の各点の
![]() が正弦波の位相です.この図からわかるように,位置が1波長進むと位相は
が正弦波の位相です.この図からわかるように,位置が1波長進むと位相は ![]() 遅れます.また,時間が1周期進むと位相は
遅れます.また,時間が1周期進むと位相は ![]() 進みます.
進みます.
このSectionの最後に,負の方向に進む正弦波を表す式を与えておきます.この式は,上の議論と全く同様に導出できますが,簡単に伝播速度 ![]() を
を ![]() に置き換えるだけでも求められます.
に置き換えるだけでも求められます.
5.2 1次元一般波動
波形が形を変えずに,一定の速さ ![]() で正の方向に進む波動を考えましょう.ただし,波形は任意のものとします.原点における時刻
で正の方向に進む波動を考えましょう.ただし,波形は任意のものとします.原点における時刻 ![]() での波動一般量
での波動一般量
![]() は,
は,
と表せます.関数 ![]() は任意であり,原点での振動の時間的変化を表します.時間が経過し,波動が
は任意であり,原点での振動の時間的変化を表します.時間が経過し,波動が ![]() だけ進行します.そのときの時刻を
だけ進行します.そのときの時刻を ![]() とします.状況を図に示します.
とします.状況を図に示します.
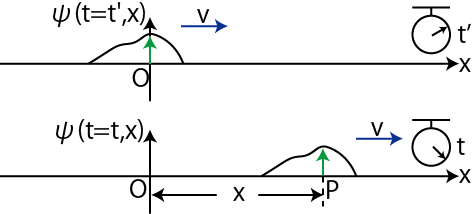
Figure5.4: 1次元一般波動
原点 ![]() の波動一般量が,原点から
の波動一般量が,原点から ![]() 離れた点
離れた点 ![]() に伝わるのに,時間
に伝わるのに,時間
![]() だけかかります.したがって,
だけかかります.したがって,
の関係があります.以上のことをまとめると,
"時刻 ![]() における点
における点 ![]() の波動一般量は,時刻
の波動一般量は,時刻
![]() における原点
における原点 ![]() の波動一般量に等しくなります."
の波動一般量に等しくなります."
ということになります.故に,1次元一般波動を表す式は,
ですから,
となります.ここで,![]() が
が
![]() の全く任意の関数であることに注意しましょう.このとき,時間
の全く任意の関数であることに注意しましょう.このとき,時間 ![]() を固定すると,その瞬間における
を固定すると,その瞬間における ![]() は波形を表しますが,この波形は縦軸が波動一般量の波形です.
は波形を表しますが,この波形は縦軸が波動一般量の波形です.![]() が変位の場合に限り,実際に目に見える波形に一致します.一方,位置
が変位の場合に限り,実際に目に見える波形に一致します.一方,位置 ![]() を固定すると,
を固定すると,![]() はその点における振動の時間的変化を表します.また,波動が負の方向に進む場合も,上記と同様な議論により波動一般量を表す式が導かれますが,ここでは簡単に波動の速さ
はその点における振動の時間的変化を表します.また,波動が負の方向に進む場合も,上記と同様な議論により波動一般量を表す式が導かれますが,ここでは簡単に波動の速さ ![]() を
を ![]() に置き換えるだけで求めることができます.その結果は次のようになります.
に置き換えるだけで求めることができます.その結果は次のようになります.
以上のような波動を1次元一般波動と呼ぶことにしましょう.ここで,正弦波も1次元一般波動の形になっていることは明らかです.また,余弦関数を用いても正弦波を表すことができます.これは初期位相を
![]() 進めることに相当します.さらに,複素数の指数関数を用いても正弦波を表すことができます.この関数の実数部は余弦関数,虚数部は正弦関数だからです.以上の正弦波をまとめて記しておきます.
進めることに相当します.さらに,複素数の指数関数を用いても正弦波を表すことができます.この関数の実数部は余弦関数,虚数部は正弦関数だからです.以上の正弦波をまとめて記しておきます.
それぞれ,![]() の前の符号が負のとき正の方向に伝わる正弦波を表し,
の前の符号が負のとき正の方向に伝わる正弦波を表し,![]() の前の符号が正のとき負の方向に伝わる正弦波を表します.
の前の符号が正のとき負の方向に伝わる正弦波を表します.
5.3 1次元波動方程式
一定の波形,一定の速さで伝搬する波動は,前のSectionで述べたように,
という形をもちます.上の式が,正の方向に進行する1次元一般波動,下の式が負の方向に進行する1次元一般波動を表します.このとき,![]() が満たす方程式を求めてみましょう.
が満たす方程式を求めてみましょう.
まず,正の方向に進む波動について調べてみます.
とおき,![]() の
の ![]() についての2次導関数を求めてみます.
についての2次導関数を求めてみます.
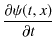 |
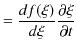 |
|
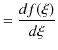 |
||
 |
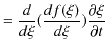 |
|
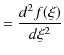 |
続けて,![]() の
の ![]() についての2次導関数も求めてみます.
についての2次導関数も求めてみます.
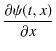 |
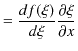 |
|
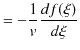 |
||
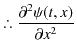 |
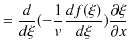 |
|
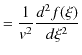 |
故に,次の1次元波動方程式といわれる,波動についての基礎方程式が成立します.
次に,負の方向に進む波動について調べてみます.
とおき,![]() の
の ![]() についての2次導関数を求めてみます.
についての2次導関数を求めてみます.
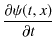 |
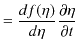 |
|
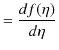 |
||
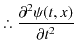 |
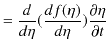 |
|
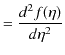 |
続けて,![]() の
の ![]() についての2次導関数も求めてみます.
についての2次導関数も求めてみます.
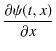 |
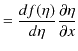 |
|
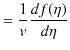 |
||
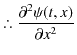 |
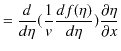 |
|
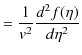 |
したがって,負の方向に進む波動についても,1次元波動方程式(5.1)式が,やはり成立します.
また,
の形の ![]() も1次元波動方程式(5.1)式を満たします.このことを,次のように確かめておきます.
も1次元波動方程式(5.1)式を満たします.このことを,次のように確かめておきます.![]() の
の ![]() についての2次導関数を求めてみます.
についての2次導関数を求めてみます.
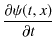 |
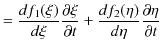 |
|
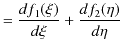 |
||
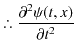 |
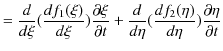 |
|
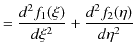 |
続けて,![]() の
の ![]() についての2次導関数も求めてみます.
についての2次導関数も求めてみます.
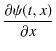 |
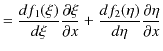 |
|
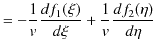 |
||
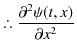 |
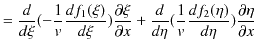 |
|
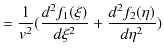 |
故に,![]() は1次元波動方程式(5.1)式を満たすことが確認されました.
は1次元波動方程式(5.1)式を満たすことが確認されました.
逆に,1次元波動方程式(5.1)式を満たす関数は,
のいずれかの形をもつことを示しておきます.
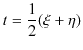 |
||
ですから,
の関係があります.![]() の
の ![]() についての2次導関数を求めてみます.
についての2次導関数を求めてみます.
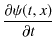 |
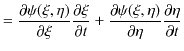 |
|
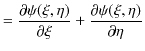 |
||
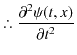 |
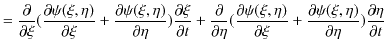 |
|
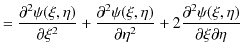 |
![]() の
の ![]() についての2次導関数も求めてみます.
についての2次導関数も求めてみます.
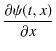 |
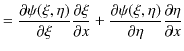 |
|
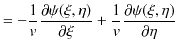 |
||
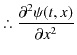 |
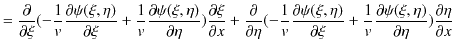 |
|
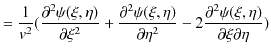 |
これらを1次元波動方程式(5.1)式に代入して計算します.
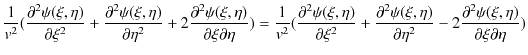 |
||
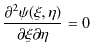 |
最後の式を ![]() について積分すると,
について積分すると,
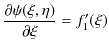
となります.ただし,
![]() は
は ![]() に依らず,
に依らず,![]() の任意の関数です.この式を
の任意の関数です.この式を ![]() について積分し,計算すると次式を得ます.
について積分し,計算すると次式を得ます.
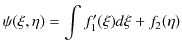 |
||
![]() はそれぞれ
はそれぞれ
![]() の任意の関数です.したがって,恒等的に 0 でも可です.よって,1次元波動方程式(5.1)式を満たす関数は,1次元一般波動の形,
の任意の関数です.したがって,恒等的に 0 でも可です.よって,1次元波動方程式(5.1)式を満たす関数は,1次元一般波動の形,
をもつことが導出されました.また,正弦波は1次元一般波動の一部として含まれるので,1次元波動方程式の1つの解として,正弦波(正弦関数,余弦関数,複素数の指数関数でそれぞれ表現されます.)があることにも注意しておきましょう.
5.4 3次元一般平面波
3次元一般平面波を考えましょう.単位ベクトル ![]() の向きに一定の速度
の向きに一定の速度
![]() で進む平面波の波面の方程式は,(ただし,時刻
で進む平面波の波面の方程式は,(ただし,時刻 ![]() において平面は原点を通る場合を考えます.)
において平面は原点を通る場合を考えます.)
です.ただし,波形は形を変えずに進行しますが,波形は任意のものとします.原点を通る平面における時刻 ![]() での波動一般量
での波動一般量
![]() は,
は,
です.関数 ![]() は任意であり,原点を含む平面での波動一般量
は任意であり,原点を含む平面での波動一般量
![]() を次の図のように示しておきます.(青枠の平面です.)時間が経過し,平面波が
を次の図のように示しておきます.(青枠の平面です.)時間が経過し,平面波が
![]() 進行します.(緑枠の平面です.)そのときの時刻を
進行します.(緑枠の平面です.)そのときの時刻を ![]() とします.
とします.
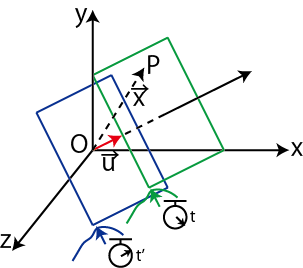
Figure5.5: 3次元一般平面波
原点 ![]() を含む平面上の波動一般量
を含む平面上の波動一般量
![]() が,原点から
が,原点から
![]() 離れた平面上の点
離れた平面上の点 ![]() に伝わるのに,時間,
に伝わるのに,時間,
![$\displaystyle \dfrac{\vec{u}\cdot\vec{x}}{v}[s]$](ja_Chapter5_WaveEquation_images/img137.png)
だけかかります.したがって,
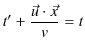 |
||
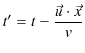 |
の関係があります.以上のことをまとめると,
"時刻 ![]() における点
における点 ![]() を含む平面上の波動一般量は時刻
を含む平面上の波動一般量は時刻
![$ (t-\dfrac{\vec{u}\cdot\vec{x}}{v})[s]$](ja_Chapter5_WaveEquation_images/img141.png) における原点
における原点 ![]() を含む平面上の波動一般量に等しくなります."
を含む平面上の波動一般量に等しくなります."
ということになります.故に,3次元一般平面波を表す式は,
![$ (t-\dfrac{\vec{u}\cdot\vec{x}}{v})[s]$](ja_Chapter5_WaveEquation_images/img141.png) における原点 における原点 |
ですから,
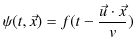
となります.ここで,波動が負の方向に進む場合も,上記と同様な議論により波動一般量を表す式が導けますが,ここでは簡単に伝搬速度 ![]() を
を ![]() に置き換えるだけで求めておきます.その結果は次のようになります.
に置き換えるだけで求めておきます.その結果は次のようになります.
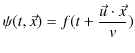
以上が,3次元一般平面波を表す式です.
3次元正弦波は3次元一般平面波の一種になります.正弦関数を使った正の方向に進行する正弦波については,表式は次のようになります.
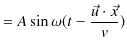 |
||
ここで,
として波数ベクトルを表記すると,このベクトルは大きさが波数を示し,向きは波動の進行方向を表します.このとき,
![]() は,
は,
となります.負の方向に進行する波動も含めて,他の3次元正弦波も同じように導出できます.3次元正弦波をまとめておきます.
5.5 3次元波動方程式
一定の波形,一定の速さで伝搬する3次元一般平面波は,前のSectionで述べたように,
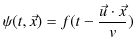 |
|
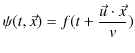 |
という形をもちます.上の式が,正の方向に進行する3次元一般平面波,下の式が負の方向に進行する3次元一般平面波を表します.このとき,
![]() が満たす方程式を求めてみましょう.
が満たす方程式を求めてみましょう.
まず,正の方向に進む波動について調べてみます.
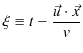
とおき,
![]() の
の ![]() についての2次導関数を求めてみます.
についての2次導関数を求めてみます.
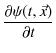 |
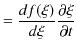 |
|
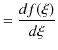 |
||
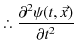 |
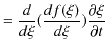 |
|
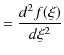 |
続けて,
![]() の
の ![]() についての2次導関数も求めてみます.
についての2次導関数も求めてみます.
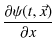 |
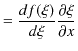 |
|
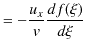 |
||
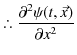 |
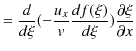 |
|
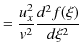 |
![]() についても同様です.故に,
についても同様です.故に,
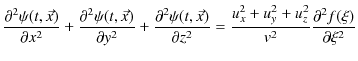
ですが,![]() は単位ベクトルであり,右辺の
は単位ベクトルであり,右辺の ![]() の
の ![]() についての2階微分を
についての2階微分を
![]() の時間の2階微分でおきかえると,
の時間の2階微分でおきかえると,
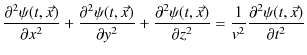
となります.したがって,次の3次元波動方程式といわれる,3次元一般平面波についての基礎方程式が成立します.
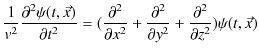
ここで,記号ナブラ ![]() ,
,
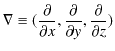
を導入すると,
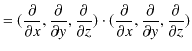 |
||
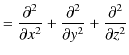 |
となりますので,3次元波動方程式は,
と表すことができます.
次に,負の方向に進む波動について調べてみます.
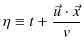
とおき,
![]() の
の ![]() についての2次導関数を求めてみます.
についての2次導関数を求めてみます.
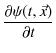 |
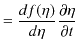 |
|
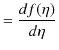 |
||
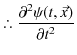 |
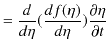 |
|
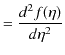 |
続けて,
![]() の
の ![]() についての2次導関数も求めてみます.
についての2次導関数も求めてみます.
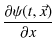 |
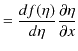 |
|
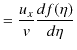 |
||
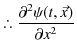 |
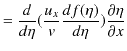 |
|
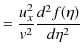 |
![]() についても同様です.
についても同様です.
![]() の
の ![]() と
と ![]() についての2次の導関数の表式が正の方向に進行する場合の
についての2次の導関数の表式が正の方向に進行する場合の ![]() を
を ![]() で置き換えたものなので,3次元波動方程式(5.2)の導出は前述のものと同様になります.
で置き換えたものなので,3次元波動方程式(5.2)の導出は前述のものと同様になります.
また,
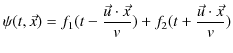
の形の
![]() も3次元波動方程式(5.2)式を満たします.このことを,次のように確かめておきます.
も3次元波動方程式(5.2)式を満たします.このことを,次のように確かめておきます.
![]() の
の ![]() についての2次導関数を求めてみます.
についての2次導関数を求めてみます.
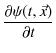 |
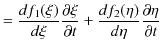 |
|
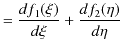 |
||
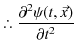 |
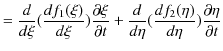 |
|
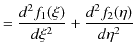 |
続けて,
![]() の
の ![]() についての2次導関数も求めてみます.
についての2次導関数も求めてみます.
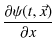 |
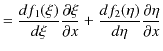 |
|
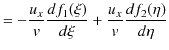 |
||
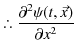 |
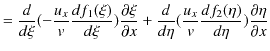 |
|
 |
![]() についても同様です.故に,
についても同様です.故に,
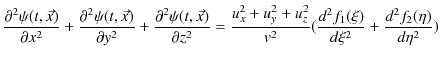
ですが,![]() は単位ベクトルであり,右辺の括弧の中を
は単位ベクトルであり,右辺の括弧の中を
![]() の時間の2階微分でおきかえると,
の時間の2階微分でおきかえると,
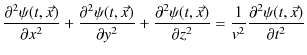
となります.故に,
![]() は3次元波動方程式(5.2)式を満たすことが確認されました.
は3次元波動方程式(5.2)式を満たすことが確認されました.
逆に,3次元波動方程式(5.2)式を満たす関数は,
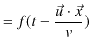 |
||
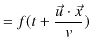 |
||
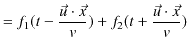 |
のいずれかの形をもつことを示しておきます.
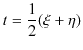 |
||
なので,
となります.
![]() の
の ![]() についての2次導関数を求めてみます.
についての2次導関数を求めてみます.
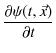 |
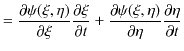 |
|
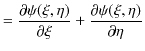 |
||
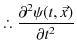 |
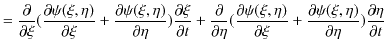 |
|
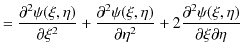 |
![]() の
の ![]() についての2次導関数も求めてみます.
についての2次導関数も求めてみます.
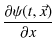 |
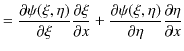 |
|
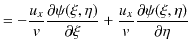 |
||
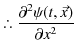 |
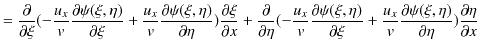 |
|
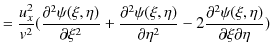 |
![]() についても同様な式が得られます.これらを3次元波動方程式(5.2)式に代入して計算します.
についても同様な式が得られます.これらを3次元波動方程式(5.2)式に代入して計算します.
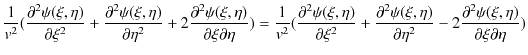 |
||
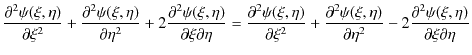 |
||
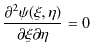 |
最後の式を ![]() について積分すると,
について積分すると,
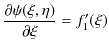
となります.ただし,
![]() は
は ![]() を含まない
を含まない ![]() の任意の関数です.この式を
の任意の関数です.この式を ![]() について積分し,計算していきます.
について積分し,計算していきます.
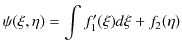 |
||
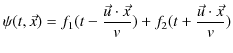 |
![]() はそれぞれ
はそれぞれ
![]() の任意の関数です.したがって,恒等的に 0 でも可です.よって,3次元波動方程式(5.2)式を満たす関数は,3次元一般波動の形,
の任意の関数です.したがって,恒等的に 0 でも可です.よって,3次元波動方程式(5.2)式を満たす関数は,3次元一般波動の形,
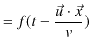 |
||
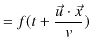 |
||
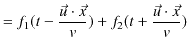 |
をもつことが導出されました.また,正弦波は3次元一般波動の一部として含まれるので,3次元波動方程式の1つの解として,正弦波(正弦関数,余弦関数,複素数の指数関数でそれぞれ表現されます.)があることにも注意しておきましょう.
次に,3次元球面波が1次元波動方程式(5.1)式と同形の方程式の解として得られることを示します.便宜上,波源を原点におきます.点
![]() の波源からの距離
の波源からの距離 ![]() は,
は,
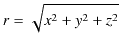
です.故に,次の関係があることがわかります.
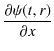 |
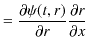 |
|
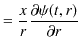 |
||
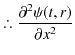 |
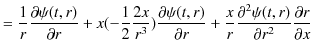 |
|
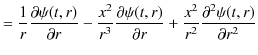 |
![]() についても,同様な式が得られます.したがって,次式を得ます.
についても,同様な式が得られます.したがって,次式を得ます.
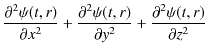 |
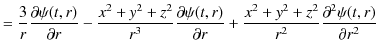 |
|
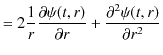 |
||
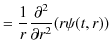 |
最後の式を,3次元波動方程式(5.2)式に代入して変形します.
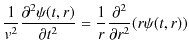 |
||
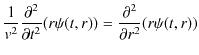 |
これは,1次元波動方程式(5.1)式において,![]() を
を
![]() で置き換えた式なので,その解は次の通りです.
で置き換えた式なので,その解は次の通りです.
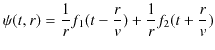 |
最後の式の右辺第1項は,波源からあらゆる方向へ速さ ![]() で伝わる波動を,右辺第2項はあらゆる方向から速さ
で伝わる波動を,右辺第2項はあらゆる方向から速さ ![]() で波源に集まる波動を表しています.また,それぞれの項に
で波源に集まる波動を表しています.また,それぞれの項に ![]() の逆数が含まれているのは,波源から離れると振幅が減少することを示しています.
の逆数が含まれているのは,波源から離れると振幅が減少することを示しています.