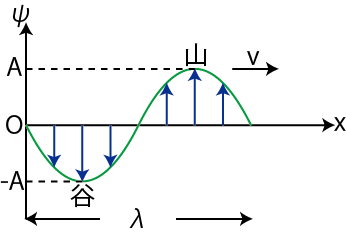
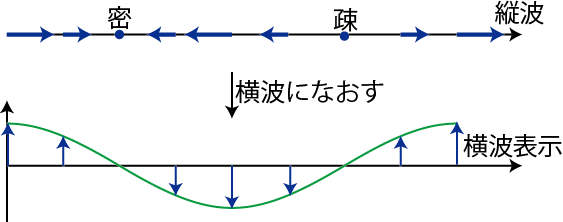
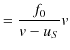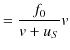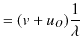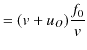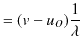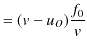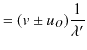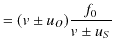横軸の ![]() は,媒質の位置を示しています.また,図の
は,媒質の位置を示しています.また,図の
![]() を波長,つりあいの位置から測った山の高さ,すなわち波動一般量の最大値
を波長,つりあいの位置から測った山の高さ,すなわち波動一般量の最大値 ![]() を振幅といいます.媒質の各点が1振動する時間,すなわち各点の振動の周期を,波動の周期
を振幅といいます.媒質の各点が1振動する時間,すなわち各点の振動の周期を,波動の周期 ![]() といい,
といい,![]() あたりの媒質の各点の振動の回数を,波動の振動数
あたりの媒質の各点の振動の回数を,波動の振動数 ![]() (ヘルツ)
(ヘルツ)![]() といいます.波源の周期・振動数は各点の周期・振動数と一致します.伝搬に伴う減衰がない場合は,振幅も一致します.ここで,振動数
といいます.波源の周期・振動数は各点の周期・振動数と一致します.伝搬に伴う減衰がない場合は,振幅も一致します.ここで,振動数 ![]() は周期
は周期 ![]() の逆数です.
の逆数です.
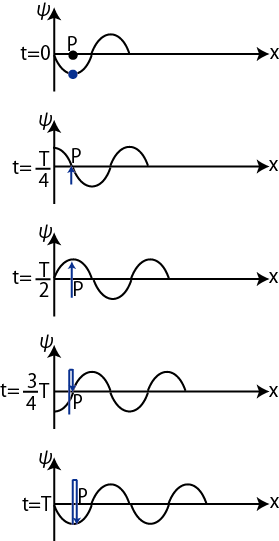
また,
"媒質のある点 ![]() が1振動する時間,周期
が1振動する時間,周期 ![]() の間に,波動は1波長
の間に,波動は1波長
![]() 進みます."
進みます."
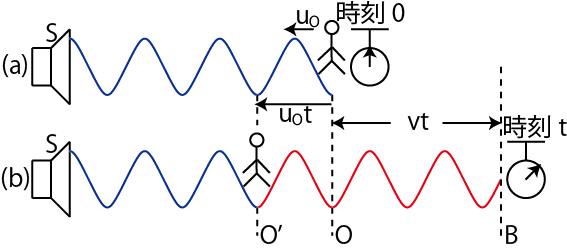
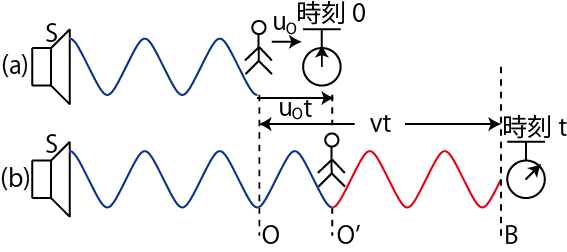
という関係が成立します.この関係は作図により,図 "正弦波2" のように確認されます.したがって,
という関係式が成立します.