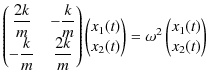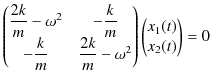Chapter3 例2(連成振動)
3.1 2粒子系の連成振動
これまでのChapterで取り扱ってきた振動は1物体に関するものでした.ここでは3本のばねで繋いだ2粒子の運動を取り扱ってみます.このような系の運動を2粒子系の連成振動といいます.
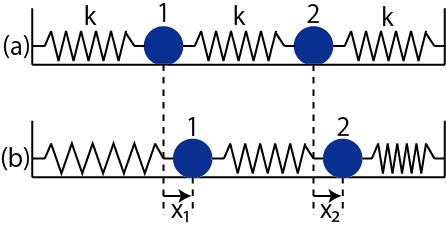
Figure3.1: 連成振動
図の(a)は,つりあいの状態です.このとき,ばねは3本とも自然長であるとします.床に摩擦はなく,粒子は質点とみなすことができ,質量は2つとも ![]() とします.また,ばねの質量は無視でき,ばね定数は3本とも
とします.また,ばねの質量は無視でき,ばね定数は3本とも ![]() です.図の(b)は,2粒子がつりあいの位置からずれた状態ですが,その変位はそれぞれ
です.図の(b)は,2粒子がつりあいの位置からずれた状態ですが,その変位はそれぞれ
![]() です.以上の状況において,図の(b)の2物体に対して運動方程式を立てると,それぞれ次のようになります.ただし,右向きを正とします.
です.以上の状況において,図の(b)の2物体に対して運動方程式を立てると,それぞれ次のようになります.ただし,右向きを正とします.
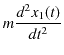 |
||
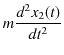 |
右辺を計算して,
です.これは連立2階微分方程式であり,次のように解きます.(3.1)式+(3.2)式と(3.1)式-(3.2)式より,
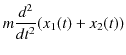 |
||
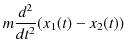 |
が得られます.ここで,
と,
とおくと,方程式は,
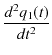 |
||
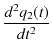 |
となります.このようにすると,座標
![]() についての調和振動子の微分方程式なので,解はわかっています.調和振動子に帰着させるため新しく選んだ座標を基準座標といいます.このとき,
についての調和振動子の微分方程式なので,解はわかっています.調和振動子に帰着させるため新しく選んだ座標を基準座標といいます.このとき,
です.ただし,
![]() は定数です.
は定数です.
![]() は,
は,
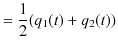 |
||
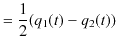 |
により求められます.
連立2階線形微分方程式(3.1)式と(3.2)式を,行列を使った方法で解いてみましょう.まず,微分方程式を,
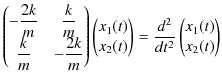
と表します.ここで,
とおきます.(複素数を使っていますが,後で実数部をとります.)このような振動を基準振動といいます.このとき,上の行列の方程式は,
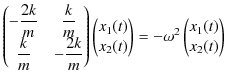
したがって,
となります.(3.3)式の中の各行列を文字で表し,
としておきます.ここで,文字の上の記号バーは,それが行列であることを表しています.(3.3)式より,
となります.(3.3)式,すなわち(3.4)式は固有値方程式です.(3.5)式で,
![]() が 0 でない解をもつためには,左辺の2×2の行列が逆行列をもたないことが必要十分条件です.したがって,2×2の行列の行列式が 0 になります.すなわち,
が 0 でない解をもつためには,左辺の2×2の行列が逆行列をもたないことが必要十分条件です.したがって,2×2の行列の行列式が 0 になります.すなわち,
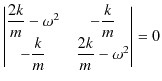
です.これを計算すると,
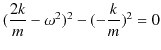 |
||
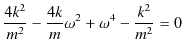 |
||
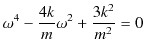 |
||
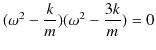 |
||
となります.ただし,
とおきました.
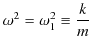
を(3.5)式に代入すると,
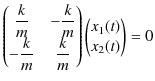
すなわち,
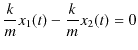 |
||
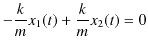 |
ですから,
となります.故に,解は,
ですが,実数部をとって,
とします.また,対応する固有ベクトルは,
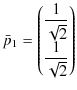
です.一方,
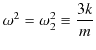
を(3.5)式に代入すると,
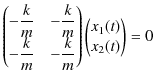 |
||
 |
||
となります.故に,解は,
ですが,実数部をとって,
とします.また,対応する固有ベクトルは,
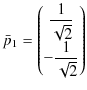
です.以上,導出された解は(3.3)式の特別な解です.一般解にするには,4個の任意定数を含まなければなりません.そこで,
をつくってみると,これがもとの微分方程式,
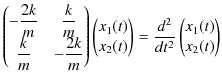
を満たすことは,次のように確かめられます.まず,左辺は次のように計算されます.
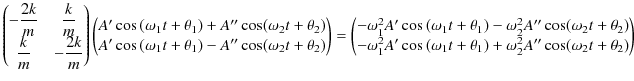
一方,右辺は次のようになります.
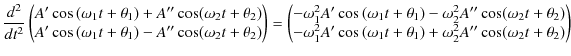
したがって,(3.6)式と(3.7)式が連立微分方程式の一般解です.
以上で解が求められたのですが,行列 ![]() を対角化して,基準座標を導出する手順を見ておくことにします.2つの固有ベクトルから直交行列
を対角化して,基準座標を導出する手順を見ておくことにします.2つの固有ベクトルから直交行列 ![]() をつくると次のようになります.
をつくると次のようになります.
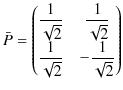
直交行列を使って,行列 ![]() を対角化します.(3.4)式,
を対角化します.(3.4)式,
より,
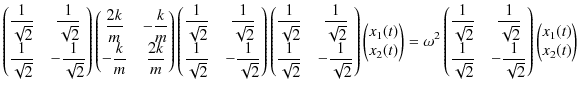 |
||
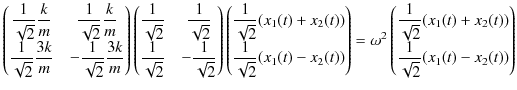 |
||
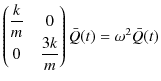 |
となります.ここで,
![]() は
は ![]() の転置行列であり,
の転置行列であり,
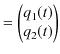 |
||
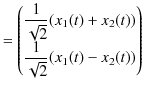 |
は基準座標です.