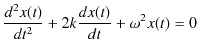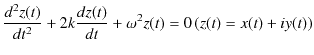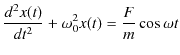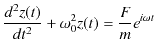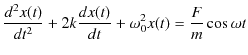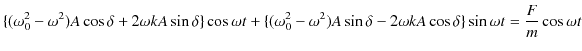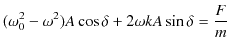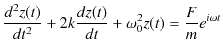J Simplicity 例1（減衰振動と強制振動）

J Simplicity

Chapter2 例1（減衰振動と強制振動）

2.1 減衰振動

振動という現象の最も基本となる1次元調和振動子の運動方程式は，

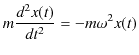
$\displaystyle m\dfrac{d^{2}x(t)}{dt^{2}}=-m\omega^{2}x(t)$

でした．右辺の力は復元力です．ここで，速さに比例する抵抗力が働く場合を考えます．便宜上，比例定数はとおきます．このとき，振動はだんだん減衰していき，最後には止まることになります．このような振動を，減衰振動といいます．運動方程式は，

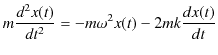
$\displaystyle m\dfrac{d^{2}x(t)}{dt^{2}}=-m\omega^{2}x(t)-2mk\dfrac{dx(t)}{dt}$

すなわち，

$\displaystyle \dfrac{d^{2}x(t)}{dt^{2}}+2k\dfrac{dx(t)}{dt}+\omega^{2}x(t)=0$

(2.1)

となります．(2.1)式の微分方程式の解法として，複素数を使った方法を採用します．複素数の微分方程式を解き，その解の実数部がもとの方程式の解になります．すなわち，

$\displaystyle \dfrac{d^{2}z(t)}{dt^{2}}+2k\dfrac{dz(t)}{dt}+\omega^{2}z(t)=0\,(z(t)=x(t)+iy(t))$

(2.2)

という(2.1)式と同形の複素数についての微分方程式(2.2)式を解き，その解の実数部がもとの(2.1)式の解になります．ただし，とは実数で，が実数部，が虚数部です．ここで，

$\displaystyle z(t)=\alpha e^{\lambda t}$

とおいてみます．このとき， $\alpha$ も $\lambda$ も複素数です．(2.2)式は次のように変形されます．

	$\displaystyle \lambda^{2}\alpha e^{\lambda t}+2k\lambda\alpha e^{\lambda t}+\omega^{2}\alpha e^{\lambda t}=0$
$% latex2html id marker 1164 $\displaystyle \therefore$$	$\displaystyle \lambda^{2}+2k\lambda+\omega^{2}=0$

したがって，

$\displaystyle \lambda=-k\pm\sqrt{k^{2}-\omega^{2}}$

(2.3)

となります．(2.3)式について，3つの場合を考え，解を求めます．

　まず，

$\displaystyle k^{2}-\omega^{2}<0$

の場合を考えます．つまり，復元力に対して抵抗力が比較的小さい場合です．このとき，

$\displaystyle \omega'^{2}\equiv\omega^{2}-k^{2}$

とおくと，(2.3)式は，

$\displaystyle \lambda=-k\pm i\omega'$

となります．したがって，

$\displaystyle z(t)$	$\displaystyle =\alpha_{1}e^{-kt}e^{i\omega't}+\alpha_{2}e^{-kt}e^{-i\omega't}$
	$\displaystyle =(a_{1}+ib_{1})e^{-kt}(\cos\omega't+i\sin\omega't)+(a_{2}+ib_{2})e^{-kt}(\cos\omega't-i\sin\omega't)$
	$\displaystyle =\{(-b_{1}+b_{2})e^{-kt}\sin\omega't+(a_{1}+a_{2})e^{-kt}\cos\omega't\}+i\{(a_{1}-a_{2})e^{-kt}\sin\omega't+(b_{1}+b_{2})e^{-kt}\cos\omega't\}$

となります．ただし， $a_{1},b_{1},a_{2},b_{2}$ は実数です．の実数部をとって，(2.1)式の解は，（ $A_{1}\equiv-b_{1}+b_{2},A_{2}\equiv a_{1}+a_{2}$ とおいて，）

$\displaystyle x(t)$	$\displaystyle =A_{1}e^{-kt}\sin\omega't+A_{2}e^{-kt}\cos\omega't$
	$\displaystyle =Ae^{-kt}(a\sin\omega't+b\cos\omega't)$

です．ただし，は実定数です．さらに変形して，

$\displaystyle x(t)=Ae^{-kt}A'\sin⁡(\omega't+\theta_{0})$

となります．ただし，

	$\displaystyle A'=\sqrt{a^{2}+b^{2}}$
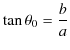	$\displaystyle \tan\theta_{0}=\dfrac{b}{a}$

です．よって，を実定数として，解は，

$\displaystyle x(t)=Be^{-kt}\sin⁡(\omega't+\theta_{0})$

となります．振動しながら指数関数的に減衰することがわかります．

　次に，

$\displaystyle k^{2}-\omega^{2}>0$

の場合を考えます．つまり，復元力に対して抵抗力が比較的大きい場合です．このとき，

$\displaystyle \lambda_{1}=k-\sqrt{k^{2}-\omega^{2}}$
$\displaystyle \lambda_{2}=k+\sqrt{k^{2}-\omega^{2}}$

とおくと，複素数の解は，

$\displaystyle z(t)=A_{1}e^{-\lambda_{1}t}+A_{2}e^{-\lambda_{2}t}$

です．複素数 $A_{1},A_{2}$ の実数部を $B_{1},B_{2}$ とおいて，

$\displaystyle x(t)=B_{1}e^{-\lambda_{1}t}+B_{2}e^{-\lambda_{2}t}$

が解になります．どちらの項も振動せずに指数関数的に減衰しますが，これを過減衰の状態といいます．

　最後に，

$\displaystyle k^{2}-\omega^{2}=0$

の場合を考えます．このとき，解は，

$\displaystyle z(t)=\alpha e^{-kt}$

ですが，２階の線形微分方程式を取り扱っているので，このままでは一般解にはできません．そこで，

$\displaystyle z(t)=\alpha(t)e^{-kt}$

とおいて，(2.2)式に代入して計算します．ここで，

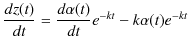	$\displaystyle \dfrac{dz(t)}{dt}=\dfrac{d\alpha(t)}{dt}e^{-kt}-k\alpha(t)e^{-kt}$
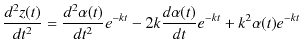	$\displaystyle \dfrac{d^{2}z(t)}{dt^{2}}=\dfrac{d^{2}\alpha(t)}{dt^{2}}e^{-kt}-2k\dfrac{d\alpha(t)}{dt}e^{-kt}+k^{2}\alpha(t)e^{-kt}$

なので，

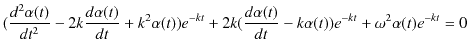	$\displaystyle (\dfrac{d^{2}\alpha(t)}{dt^{2}}-2k\dfrac{d\alpha(t)}{dt}+k^{2}\al... ...{-kt}+2k(\dfrac{d\alpha(t)}{dt}-k\alpha(t))e^{-kt}+\omega^{2}\alpha(t)e^{-kt}=0$
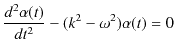$% latex2html id marker 1218 $\displaystyle \therefore$$	$\displaystyle \dfrac{d^{2}\alpha(t)}{dt^{2}}-(k^{2}-\omega^{2})\alpha(t)=0$
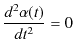$% latex2html id marker 1220 $\displaystyle \therefore$$	$\displaystyle \dfrac{d^{2}\alpha(t)}{dt^{2}}=0$
$% latex2html id marker 1222 $\displaystyle \therefore$$	$\displaystyle \alpha(t)=Ct+D$

となります．ただし，とは積分定数です．したがって，(2.2)式の一般解は，

$\displaystyle z(t)=(Ct+D)e^{-kt}$

となります．定数との実数部を，改めてととおくと，(2.1)式の解は，

$\displaystyle x(t)=(Ct+D)e^{-kt}$

です．この場合も指数関数的に減衰します．この状態を臨界減衰といいます．

2.2 強制振動

角振動数 $\omega_{0}[rad/s]$ の１次元調和振動子に角振動数 $\omega[rad/s]$ の周期的な外力，

$\displaystyle F\cos\omega t$

が働く場合を考えましょう．このような状況の振動を強制振動といいます．運動方程式は次のようになります．

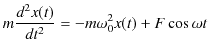
$\displaystyle m\dfrac{d^{2}x(t)}{dt^{2}}=-m\omega_{0}^{2}x(t)+F\cos\omega t$

少し変形して，次のようになります．

$\displaystyle \dfrac{d^{2}x(t)}{dt^{2}}+\omega_{0}^{2}x(t)=\dfrac{F}{m}\cos\omega t$

(2.4)

(2.4)式は2階の線形微分方程式です．これを線形微分方程式の一般論にしたがって解きます．まず，右辺を 0 とおいた同次方程式は，調和振動子の微分方程式そのものですので，その解は，

$\displaystyle x_{0}(t)=A\sin⁡(\omega_{0}t+\theta_{0})$

です．次に，(2.4)式の特解を求めます．特解としては外力と同じ周期の振動が予想されるので，

$\displaystyle x_{1}(t)=b\cos\omega t$

とおいて，(2.4)式に代入して計算します．

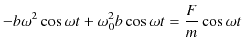	$\displaystyle -b\omega^{2}\cos\omega t+\omega_{0}^{2}b\cos\omega t=\dfrac{F}{m}\cos\omega t$
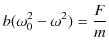$% latex2html id marker 1257 $\displaystyle \therefore$$	$\displaystyle b(\omega_{0}^{2}-\omega^{2})=\dfrac{F}{m}$
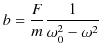$% latex2html id marker 1259 $\displaystyle \therefore$$	$\displaystyle b=\dfrac{F}{m}\dfrac{1}{\omega_{0}^{2}-\omega^{2}}$
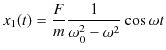$% latex2html id marker 1261 $\displaystyle \therefore$$	$\displaystyle x_{1}(t)=\dfrac{F}{m}\dfrac{1}{\omega_{0}^{2}-\omega^{2}}\cos\omega t$

故に，一般解は同次方程式の解と特解の和なので，

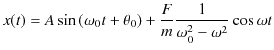
$\displaystyle x(t)=A\sin⁡(\omega_{0}t+\theta_{0})+\dfrac{F}{m}\dfrac{1}{\omega_{0}^{2}-\omega^{2}}\cos\omega t$

と求められます．この解の第1項は，外力が作用していないときの調和振動を表しています．第2項は外力の影響を示していますが，

$\displaystyle \omega=\omega_{0}$

の場合，振幅は無限大になります．このような状態を共鳴または共振といいます．

　強制振動の問題を，複素数を使った方法で解いてみましょう．周期的な外力として，

$\displaystyle Fe^{i\omega t}$

を加え，複素数の微分方程式を考えます．

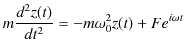
$\displaystyle m\dfrac{d^{2}z(t)}{dt^{2}}=-m\omega_{0}^{2}z(t)+Fe^{i\omega t}$

変形して，

$\displaystyle \dfrac{d^{2}z(t)}{dt^{2}}+\omega_{0}^{2}z(t)=\dfrac{F}{m}e^{i\omega t}$

(2.5)

の実数部が解なので，実質的には外力として，

$\displaystyle F\cos\omega t$

を加えていることになります．この外力は上の議論におけるものと一致しています．(2.5)式の特解を求めるために， $\alpha$ を複素数の定数として，

$\displaystyle z(t)=\alpha e^{i\omega t}$

とおき，微分方程式に代入して計算します．

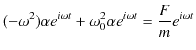	$\displaystyle (-\omega^{2})\alpha e^{i\omega t}+\omega_{0}^{2}\alpha e^{i\omega t}=\dfrac{F}{m}e^{i\omega t}$
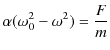$% latex2html id marker 1282 $\displaystyle \therefore$$	$\displaystyle \alpha(\omega_{0}^{2}-\omega^{2})=\dfrac{F}{m}$
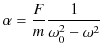$% latex2html id marker 1284 $\displaystyle \therefore$$	$\displaystyle \alpha=\dfrac{F}{m}\dfrac{1}{\omega_{0}^{2}-\omega^{2}}$

$\alpha$ が求められましたが，これは実数であることがわかりました．故に，は，

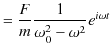$\displaystyle z(t)$	$\displaystyle =\dfrac{F}{m}\dfrac{1}{\omega_{0}^{2}-\omega^{2}}e^{i\omega t}$
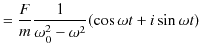	$\displaystyle =\dfrac{F}{m}\dfrac{1}{\omega_{0}^{2}-\omega^{2}}(\cos\omega t+i\sin\omega t)$

ですので，実数部をとって特解 $x_{1}(t)[m]$ は，

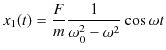
$\displaystyle x_{1}(t)=\dfrac{F}{m}\dfrac{1}{\omega_{0}^{2}-\omega^{2}}\cos\omega t$

となります．この特解は上の議論での余弦関数のものに一致しています．

2.3 抵抗力のある場合の強制振動

"減衰振動" のSectionのように，速さに比例する抵抗力を受けると同時に，"強制振動" のSectionのような外力が働く場合を考えましょう．このとき，運動方程式は次のようになります．

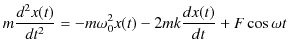
$\displaystyle m\dfrac{d^{2}x(t)}{dt^{2}}=-m\omega_{0}^{2}x(t)-2mk\dfrac{dx(t)}{dt}+F\cos\omega t$

これを変形して，

$\displaystyle \dfrac{d^{2}x(t)}{dt^{2}}+2k\dfrac{dx(t)}{dt}+\omega_{0}^{2}x(t)=\dfrac{F}{m}\cos\omega t$

(2.6)

となります．(2.6)式を線形微分方程式の一般論にしたがって解きます．まず，右辺を 0 とおいた同次方程式については，"減衰振動" のSectionで取り扱った通りです．次に，(2.6)式の特解を求めます．解としては，外力と同じ周期の振動が予想されるので，特解を，

$\displaystyle x_{1}(t)=A\cos⁡(\omega t-\delta)$

とおいて，(2.6)式に代入して計算します．

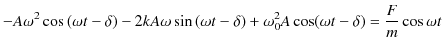	$\displaystyle -A\omega^{2}\cos⁡(\omega t-\delta)-2kA\omega\sin⁡(\omega t-\delta)+\omega_{0}^{2}A\cos(\omega t-\delta)=\dfrac{F}{m}\cos\omega t$
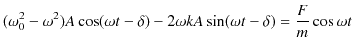$% latex2html id marker 1306 $\displaystyle \therefore$$	$\displaystyle (\omega_{0}^{2}-\omega^{2})A\cos(\omega t-\delta)-2\omega kA\sin(\omega t-\delta)=\dfrac{F}{m}\cos\omega t$
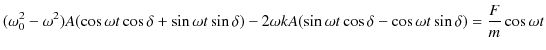$% latex2html id marker 1308 $\displaystyle \therefore$$	$\displaystyle (\omega_{0}^{2}-\omega^{2})A(\cos\omega t\cos\delta+\sin\omega t\... ...mega kA(\sin\omega t\cos\delta-\cos\omega t\sin\delta)=\dfrac{F}{m}\cos\omega t$

故に，

$\displaystyle \{(\omega_{0}^{2}-\omega^{2})A\cos\delta+2\omega kA\sin\delta\}\c... ...ega^{2})A\sin\delta-2\omega kA\cos\delta\}\sin\omega t=\dfrac{F}{m}\cos\omega t$

(2.7)

(2.7)式において，とおいた式と，(2.7)式をで微分してとおいた式より，

	$\displaystyle (\omega_{0}^{2}-\omega^{2})A\cos\delta+2\omega kA\sin\delta=\dfrac{F}{m}$	(2.8)
	$\displaystyle (\omega_{0}^{2}-\omega^{2})A\sin\delta-2\omega kA\cos\delta=0$	(2.9)

です．ここで，(2.8)× $2\omega k$ +(2.9)× $(\omega_{0}^{2}-\omega^{2})$ より，

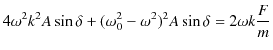	$\displaystyle 4\omega^{2}k^{2}A\sin\delta+(\omega_{0}^{2}-\omega^{2})^{2}A\sin\delta=2\omega k\dfrac{F}{m}$
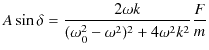$% latex2html id marker 1325 $\displaystyle \therefore$$	$\displaystyle A\sin\delta=\dfrac{2\omega k}{(\omega_{0}^{2}-\omega^{2})^{2}+4\omega^{2}k^{2}}\dfrac{F}{m}$

となります．また，(2.8)× $(\omega_{0}^{2}-\omega^{2})$ -(2.9)× $2\omega k$ より，

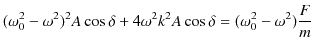	$\displaystyle (\omega_{0}^{2}-\omega^{2})^{2}A\cos\delta+4\omega^{2}k^{2}A\cos\delta=(\omega_{0}^{2}-\omega^{2})\dfrac{F}{m}$
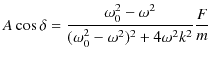$% latex2html id marker 1332 $\displaystyle \therefore$$	$\displaystyle A\cos\delta=\dfrac{\omega_{0}^{2}-\omega^{2}}{(\omega_{0}^{2}-\omega^{2})^{2}+4\omega^{2}k^{2}}\dfrac{F}{m}$

となります．故に，が以下のように求められます．

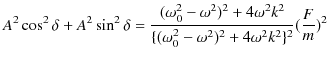	$\displaystyle A^{2}\cos^{2}\delta+A^{2}\sin^{2}\delta=\dfrac{(\omega_{0}^{2}-\o... ...2}}{\{(\omega_{0}^{2}-\omega^{2})^{2}+4\omega^{2}k^{2}\}^{2}}(\dfrac{F}{m})^{2}$
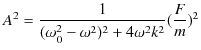$% latex2html id marker 1337 $\displaystyle \therefore$$	$\displaystyle A^{2}=\dfrac{1}{(\omega_{0}^{2}-\omega^{2})^{2}+4\omega^{2}k^{2}}(\dfrac{F}{m})^{2}$
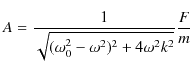$% latex2html id marker 1339 $\displaystyle \therefore$$	$\displaystyle A=\dfrac{1}{\sqrt{(\omega_{0}^{2}-\omega^{2})^{2}+4\omega^{2}k^{2}}}\dfrac{F}{m}$

$\delta[rad]$ も次のように計算できます．

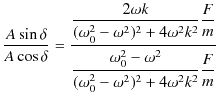	$\displaystyle \dfrac{A\sin\delta}{A\cos\delta}=\dfrac{\dfrac{2\omega k}{(\omega... ...^{2}-\omega^{2}}{(\omega_{0}^{2}-\omega^{2})^{2}+4\omega^{2}k^{2}}\dfrac{F}{m}}$
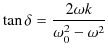$% latex2html id marker 1344 $\displaystyle \therefore$$	$\displaystyle \tan\delta=\dfrac{2\omega k}{\omega_{0}^{2}-\omega^{2}}$

　特解を求めるのに，複素数を使った方法で解いてみましょう．微分方程式，

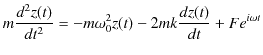
$\displaystyle m\dfrac{d^{2}z(t)}{dt^{2}}=-m\omega_{0}^{2}z(t)-2mk\dfrac{dz(t)}{dt}+Fe^{i\omega t}$

を変形して，

$\displaystyle \dfrac{d^{2}z(t)}{dt^{2}}+2k\dfrac{dz(t)}{dt}+\omega_{0}^{2}z(t)=\dfrac{F}{m}e^{i\omega t}$

(2.10)

の実数部が求める特解になります． $\alpha$ を複素数の定数として，

$\displaystyle z(t)=\alpha e^{i\omega t}$

とおき，微分方程式(2.10)式に代入して計算します．

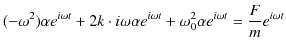	$\displaystyle (-\omega^{2})\alpha e^{i\omega t}+2k\cdot i\omega\alpha e^{i\omega t}+\omega_{0}^{2}\alpha e^{i\omega t}=\dfrac{F}{m}e^{i\omega t}$
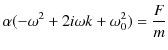$% latex2html id marker 1355 $\displaystyle \therefore$$	$\displaystyle \alpha(-\omega^{2}+2i\omega k+\omega_{0}^{2})=\dfrac{F}{m}$
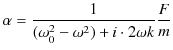$% latex2html id marker 1357 $\displaystyle \therefore$$	$\displaystyle \alpha=\dfrac{1}{(\omega_{0}^{2}-\omega^{2})+i\cdot2\omega k}\dfrac{F}{m}$

ここで，

	$\displaystyle \beta\equiv(\omega_{0}^{2}-\omega^{2})+i\cdot2\omega k$
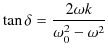	$\displaystyle \tan\delta=\dfrac{2\omega k}{\omega_{0}^{2}-\omega^{2}}$

とおきます．

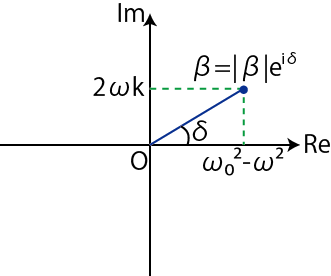
ガウス平面

Figure2.1: ガウス平面

このとき，

$\displaystyle \alpha$	$\displaystyle =\dfrac{1}{\beta}\dfrac{F}{m}$
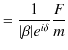$% latex2html id marker 1367 $\displaystyle \therefore\alpha$$	$\displaystyle =\dfrac{1}{\vert\beta\vert e^{i\delta}}\dfrac{F}{m}$

です．さらに，

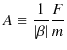
$\displaystyle A\equiv\dfrac{1}{\vert\beta\vert}\dfrac{F}{m}$

とおくと，

	$\displaystyle \alpha=Ae^{-i\delta}$
$% latex2html id marker 1372 $\displaystyle \therefore$$	$\displaystyle z(t)=\alpha e^{i\omega t}=Ae^{-i\delta}e^{i\omega t}=Ae^{i(\omega t-\delta)}$

となります．実数部をとって，特解 $x_{1}(t)[m]$ は，

$\displaystyle x_{1}(t)=A\cos(\omega t-\delta)$

となります．この特解は，上の議論での余弦関数のものに一致しています．