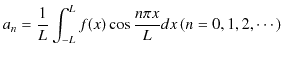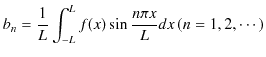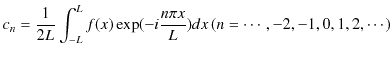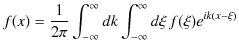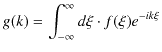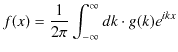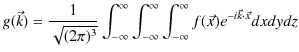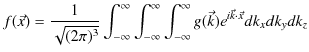Part1 振動
Chapter1 振動
1.1 調和振動子
様々な振動の中で,最も基本となる振動は調和振動子の振動です.詳細については,Report "力学" の "例(調和振動子)" のChapterを参照して下さい.ここでは簡単に復習しておきます.1次元調和振動子の運動方程式は,
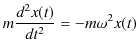
です.ここで,![]() は質量,
は質量,
![]() は角振動数です.そして,この微分方程式の解は,
は角振動数です.そして,この微分方程式の解は,
でした.ただし,![]() は振幅,
は振幅,
![]() は初期位相です.振動する物体の場合,
は初期位相です.振動する物体の場合,![]() は変位ですが,振動するものは物体に限らず,電場や磁場のようなものもあります.そこで,変位
は変位ですが,振動するものは物体に限らず,電場や磁場のようなものもあります.そこで,変位 ![]() の代わりに,
の代わりに,![]() として,全ての振動を含めた量を使うことにします.
として,全ての振動を含めた量を使うことにします.![]() のことを,振動一般量と呼ぶことにします.
のことを,振動一般量と呼ぶことにします.
最も簡単な振動は調和振動子の振動であり,その時間依存のグラフは正弦曲線になります.それに対して,複雑な振動では時間依存のグラフが綺麗な正弦曲線にはなりません.しかし,どのような振動も正弦関数と余弦関数の重ね合わせにより表されることが,証明されています.つまり,複雑な振動でも複数の調和振動子の振動に分解することができるのです.この強力な数学をフーリエ解析といいます.以下,4つのSectionにわたり,フーリエ解析一般について,その数学的エッセンスを見ていき,最後のSectionで,フーリエ解析を用いて,複雑な振動を一般的に取り扱うことにしましょう.
1.2 数学的準備1(フーリエ解析1: フーリエ級数)
これから4つののSectionでは,物理から離れて,フーリエ解析という数学の話をしていきます.さて,変数 ![]() の関数
の関数 ![]() が周期
が周期 ![]() をもつものとします.(図を見て下さい.また,この場合の変数や周期は,純粋に数学的な量です.)
をもつものとします.(図を見て下さい.また,この場合の変数や周期は,純粋に数学的な量です.)
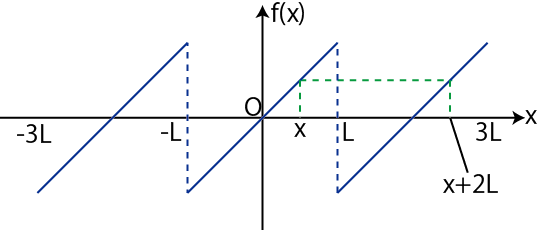
Figure1.1: 周期関数の例
すなわち,![]() は,
は,
の関係を満たす関数であるとします.(非周期的な関数の場合は,
![]() とすればよいので,以下の議論は一般性をもっています.)このとき,
とすればよいので,以下の議論は一般性をもっています.)このとき,![]() は,周期
は,周期 ![]() をもつ正弦関数と余弦関数の集まりの和によって,
をもつ正弦関数と余弦関数の集まりの和によって,
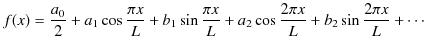
すなわち,
と展開できるとして,![]() から係数
から係数
![]() を決める公式を導いてみましょう.
を決める公式を導いてみましょう.
準備として,次の公式を証明する必要があります.
ここで,第1式と第2式の右辺の記号は,
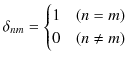
を意味し,クロネッカーのデルタといいます.さて,オイラーの公式,
より,
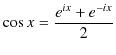 |
||
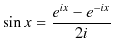 |
としておきます.このとき,(1.2)式を,以下証明していきます.
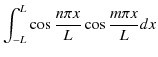 |
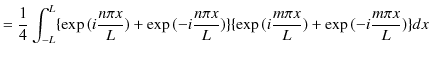 |
|
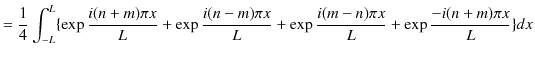 |
ここで,![]() を整数として,
を整数として,
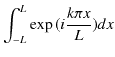 |
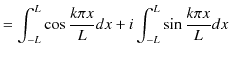 |
|
![$\displaystyle =\begin{cases}
\int_{-L}^{L}1dx+i\int_{-L}^{L}0dx=[x]_{-L}^{L}=2...
...}^{L}+i[-\dfrac{L}{k\pi}\cos\dfrac{k\pi x}{L}]_{-L}^{L}=0&(k\neq0)
\end{cases}$](ja_Chapter1_Oscillation_images/img32.png) |
なので,
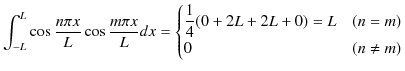
となり,(1.2)式が証明されました.(1.3)式,(1.4)式も同様に証明されます.
(1.2)式,(1.3)式,(1.4)式を用いて,(1.1)式の係数
![]() を求めましょう.まず,
を求めましょう.まず,![]() について見ていきます.(1.1)式の両辺に,
について見ていきます.(1.1)式の両辺に,
![]() をかけて,
をかけて,![]() について,
について,![]() から
から ![]() まで積分します.
まで積分します.
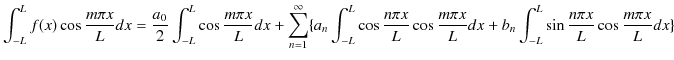
ここで,右辺第1項の積分は,![]() のとき,
のとき,
![$\displaystyle \int_{-L}^{L}\cos\dfrac{m\pi x}{L}dx=[\dfrac{L}{m\pi}\sin\dfrac{m\pi x}{L}]_{-L}^{L}=0$](ja_Chapter1_Oscillation_images/img40.png)
となり,![]() のとき,
のとき,
![$\displaystyle \int_{-L}^{L}\cos\dfrac{0\pi x}{L}dx=\int_{-L}^{L}1dx=[x]_{-L}^{L}=2L$](ja_Chapter1_Oscillation_images/img42.png)
となります.故に,
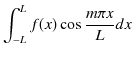 |
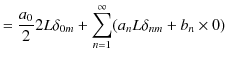 |
|
ですから,すなわち,
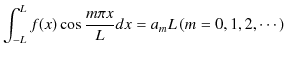
となります.![]() を
を ![]() に置き換えて,係数
に置き換えて,係数 ![]() は,
は,
と求められます.係数 ![]() についても同様に,
についても同様に,
と求められます.
(1.5)式と(1.6)式の係数をフーリエ係数といい,これらの係数を代入して得られる級数(1.1)式,
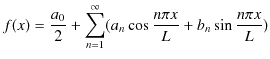
を,![]() に対するフーリエ級数といいます.フーリエ級数によって,周期的な関数を,正弦関数と余弦関数の無限級数によって表すことができるのです.
に対するフーリエ級数といいます.フーリエ級数によって,周期的な関数を,正弦関数と余弦関数の無限級数によって表すことができるのです.
1.3 数学的準備2(フーリエ解析2: 規格直交関数系)
前Sectionで導出した公式(1.2)式,(1.3)式,(1.4)式,
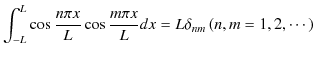 |
||
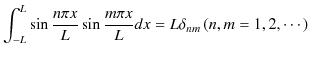 |
||
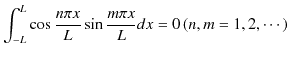 |
を系統立てて調べてみましょう.
![]() には
には ![]() の場合も含まれることを考慮に入れると,(1.2)式,(1.3)式,(1.4)式は,次のように書き換えることができます.
の場合も含まれることを考慮に入れると,(1.2)式,(1.3)式,(1.4)式は,次のように書き換えることができます.
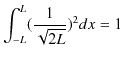 |
||
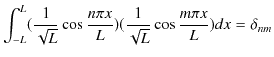 |
||
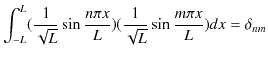 |
||
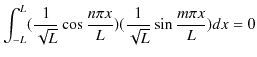 |
これらの式からわかることは,3角関数の関数列,
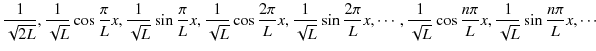
をつくってみると,どの1つの関数でも同じものを2乗して ![]() から
から ![]() まで積分すれば
まで積分すれば ![]() となり,どの異なる2つの関数をとっても,その積の,
となり,どの異なる2つの関数をとっても,その積の,![]() から
から ![]() までの積分は 0 になることがわかります.このような関数列は,区間
までの積分は 0 になることがわかります.このような関数列は,区間 ![]() において規格直交関数系をつくるといいます.
において規格直交関数系をつくるといいます.
一般化した形で述べると,区間 ![]() において,実数値をとる関数列
において,実数値をとる関数列
![]() が,
が,
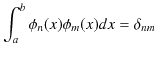
の関係を満たすとき,関数列
![]() はその区間において規格直交関数系をつくるといいます.
はその区間において規格直交関数系をつくるといいます.
1.4 数学的準備3(フーリエ解析3: 複素フーリエ級数)
フーリエ級数を使って解析を行う場合,3角関数よりも複素数の指数関数を使った方が便利な場合もあります.オイラーの公式より,前述したように,
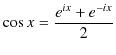 |
||
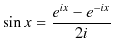 |
という関係があります.これをフーリエ級数(1.1)式,
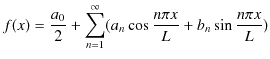
に代入して,
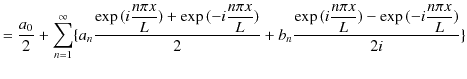 |
||
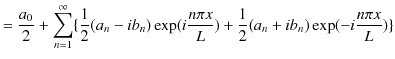 |
となります.ここで,
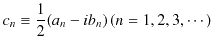 |
||
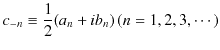 |
とおくと,
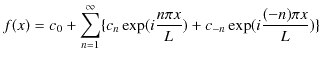
すなわち,
となります.この(1.7)式を複素フーリエ級数といいます.係数
![]() を求めると,(1.5)式,(1.6)式より,
を求めると,(1.5)式,(1.6)式より,
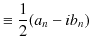 |
||
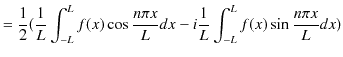 |
||
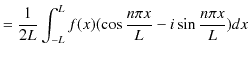 |
||
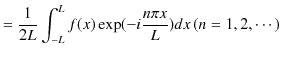 |
および,
 |
||
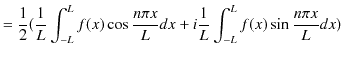 |
||
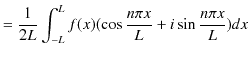 |
||
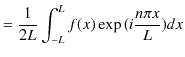 |
||
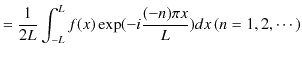 |
となります.また,
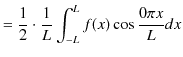 |
||
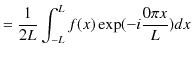 |
です.これらをまとめて,
となります.この(1.8)式を複素フーリエ係数といいます.
1.5 数学的準備4(フーリエ解析4: フーリエ積分とフーリエ変換)
周期
![]() として,非周期関数を取り扱うようにしましょう.このとき,フーリエ級数はフーリエ積分というものになります.以下に,議論していきます.
として,非周期関数を取り扱うようにしましょう.このとき,フーリエ級数はフーリエ積分というものになります.以下に,議論していきます.
周期 ![]() をもつ周期関数
をもつ周期関数 ![]() が複素フーリエ級数によって表されているものとします.複素フーリエ級数(1.7)式と複素フーリエ係数(1.8)式を再掲すると,
が複素フーリエ級数によって表されているものとします.複素フーリエ級数(1.7)式と複素フーリエ係数(1.8)式を再掲すると,
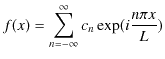 |
||
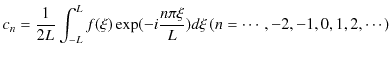 |
でした.ただし,複素フーリエ係数(1.8)式の変数は,複素フーリエ級数(1.7)式の変数 ![]() と区別するため
と区別するため ![]() と置き直してあります.(1.8)式を(1.7)式に代入して,
と置き直してあります.(1.8)式を(1.7)式に代入して,
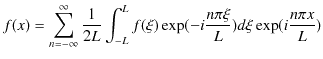
となります.ここで,
として,新しい記号を導入します.
ですから,このとき,
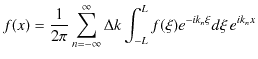
となります.ここで,
![]() として非周期関数の場合を考えることにします.このとき,
として非周期関数の場合を考えることにします.このとき,![]() は連続変数とみなせ,
は連続変数とみなせ,
![]() ですので,和を積分に変えます.
ですので,和を積分に変えます.
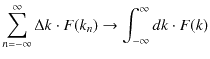
故に,
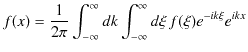
つまり,
となります.(1.9)式を複素フーリエ積分といいます.
ここで,(1.9)式において,
とおけば,
となります.このとき,(1.10)式の変換,すなわち,![]() から
から ![]() への変換をフーリエ変換といい,(1.11)式の変換,すなわち,
への変換をフーリエ変換といい,(1.11)式の変換,すなわち,![]() から
から ![]() への変換を逆フーリエ変換といいます.フーリエ変換(1.10)式は,関数
への変換を逆フーリエ変換といいます.フーリエ変換(1.10)式は,関数 ![]() を
を ![]() についての重みの分布
についての重みの分布 ![]() に分解しています.フーリエ変換(1.10)式は,フーリエ級数の場合のフーリエ係数に相当するものです.フーリエ逆変換(1.11)式は,
に分解しています.フーリエ変換(1.10)式は,フーリエ級数の場合のフーリエ係数に相当するものです.フーリエ逆変換(1.11)式は,![]() についての重み
についての重み ![]() から,関数
から,関数 ![]() に戻したものです.
に戻したものです.![]() と
と ![]() の積の積分の前の係数は,
の積の積分の前の係数は,
![]() となればよいので,式の形を
となればよいので,式の形を ![]() と
と ![]() について均等にするために,
について均等にするために,
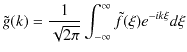 |
||
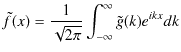 |
としてもよいことがわかります.これらの式の関数の上にあるチルダの記号は,(1.10)式と(1.11)式から区別するために付けましたが,改めてチルダを取って表記することにします.また,この段階で ![]() を
を ![]() に戻しても,混乱はしないでしょう.最終的に,フーリエ変換は,
に戻しても,混乱はしないでしょう.最終的に,フーリエ変換は,
となり,フーリエ逆変換は,
となります.
フーリエ変換とフーリエ逆変換を3次元に拡張することもできます.このとき,1次元の変数 ![]() を,3次元の変数
を,3次元の変数
![]() にします.同様に,1次元の変数
にします.同様に,1次元の変数 ![]() を,3次元の変数
を,3次元の変数
![]() にします.1次元フーリエ変換(1.12)式より,
にします.1次元フーリエ変換(1.12)式より,
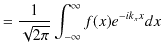 |
||
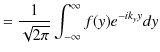 |
||
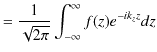 |
が成立します.これらの式を辺々掛け合わせます.
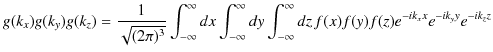
ここで,
![]() を
を
![]() と,
と,
![]() を
を
![]() と,改めてそれぞれ置き直します.このとき,次式の3次元フーリエ変換が成立します.
と,改めてそれぞれ置き直します.このとき,次式の3次元フーリエ変換が成立します.
また,1次元フーリエ逆変換(1.13)式より,
 |
||
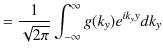 |
||
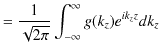 |
が成立します.これらの式を辺々掛け合わせます.

このとき,次式の3次元フーリエ逆変換が成立します.
以上のような数学をフーリエ解析といいます.フーリエ解析は振動と波動の分野だけでなく,量子力学等,物理学の研究において,幅広く使用されています.
1.6 振動のフーリエ解析
振動に話を戻して,周期 ![]() の一般的な振動の振動一般量を表す関数
の一般的な振動の振動一般量を表す関数 ![]() を,今までの数学的準備で取り扱った
を,今までの数学的準備で取り扱った ![]() と同定し,フーリエ級数で表現することを考えてみましょう.(1.1)式において,数学的な周期
と同定し,フーリエ級数で表現することを考えてみましょう.(1.1)式において,数学的な周期 ![]() を振動の時間の周期
を振動の時間の周期 ![]() に,数学的な変数
に,数学的な変数 ![]() を振動における変数である時間
を振動における変数である時間 ![]() に置き換えます.このとき,
に置き換えます.このとき,
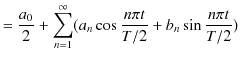 |
||
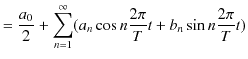 |
||
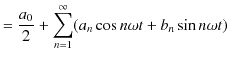 |
とすることができます.ただし,
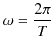
は振動の角振動数です.任意の振動が,
の角振動数をもつ調和振動子の和によって表されるのです.それぞれの角振動数についての重みであるフーリエ係数は,(1.5)式と(1.6)式より,
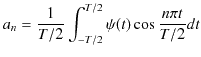 |
||
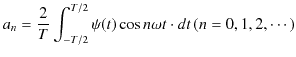 |
||
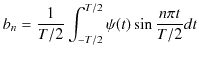 |
||
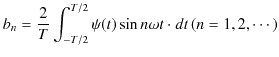 |
によって求められます.最初のSectionで述べていたこと,すなわち,任意の振動が無限個の調和振動子の振動の和に分解できることが確認されました.
周期 ![]() の一般的な振動の振動一般量を表す関数
の一般的な振動の振動一般量を表す関数 ![]() を数学的準備で取り扱った関数
を数学的準備で取り扱った関数 ![]() と同定し,複素フーリエ級数で表現することを考えてみましょう.(1.7)式において,数学的周期
と同定し,複素フーリエ級数で表現することを考えてみましょう.(1.7)式において,数学的周期 ![]() を振動の時間的周期
を振動の時間的周期 ![]() に,数学的変数
に,数学的変数 ![]() を振動における変数である時間
を振動における変数である時間 ![]() に置き換えます.このとき,
に置き換えます.このとき,
 |
||
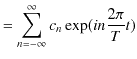 |
||
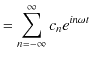 |
とすることができます.ただし,
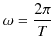
は振動の角振動数です.任意の振動が,
の角振動数をもつ調和振動子の和によって表されるのです.それぞれの角振動数についての重みであるフーリエ係数は,(1.8)式より,
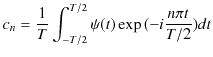 |
||
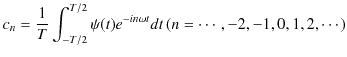 |
です.複素フーリエ級数を用いても,任意の振動が無限個の調和振動子の振動の和に分解できることが確認されました.
一般的な振動についてのフーリエ変換も考えてみましょう.前述の数学的準備におけるフーリエ変換とフーリエ逆変換を表す式は,(1.12)式と(1.13)式,
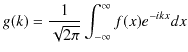 |
||
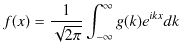 |
でした.物理的な振動の場合,振動一般量 ![]() を数学的関数
を数学的関数 ![]() と同定しましょう.さらに,(1.12)式,(1.13)式に出てくる
と同定しましょう.さらに,(1.12)式,(1.13)式に出てくる ![]() は,振動の場合,分解された調和振動子のそれぞれの角振動数
は,振動の場合,分解された調和振動子のそれぞれの角振動数
![]() という意味をもってきます.そして,数学的変数
という意味をもってきます.そして,数学的変数 ![]() を振動における変数である時間
を振動における変数である時間 ![]() に置き換えます.このとき,フーリエ変換(1.12)式は,次のようになります.
に置き換えます.このとき,フーリエ変換(1.12)式は,次のようになります.
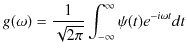
すなわち,振動の一般量 ![]() を角振動数
を角振動数
![]() の重みの分布
の重みの分布 ![]() で表しています.一方,フーリエ逆変換(1.13)式は,
で表しています.一方,フーリエ逆変換(1.13)式は,
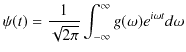
となります.この式は,分解されたそれぞれの調和振動子の振動
![]() に角振動数
に角振動数
![]() のときの重み
のときの重み ![]() をかけて重ね合わせて,振動一般量
をかけて重ね合わせて,振動一般量 ![]() に戻したものです.
に戻したものです.