Chapter9 例3（等速円運動）

9.1 等速円運動の角速度・速度・加速度

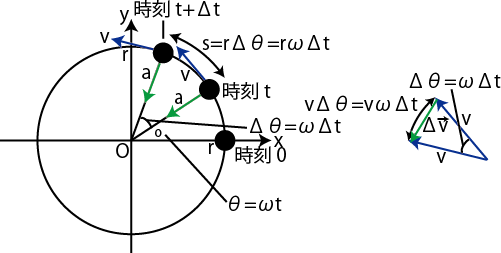
一定の速さ $ v[m/s]$ の円運動である等速円運動について考えてみましょう．この運動の例としては天井から糸で下げられた円錐振り子，回転する円盤上の物体，惑星の公転運動（厳密に言うと楕円運動ですが，近似して考えて下さい．），磁場中で円運動する荷電粒子，原子内の電子の円運動等が挙げられます．

等速円運動

Figure9.1: 等速円運動

物体と円の中心とを結ぶ動径が単位時間に回転する角を角速度と言います．すなわち，角速度は $ \omega[rad/s]$ は， $ \Delta t[s]$ あたりの回転角を $ \Delta\theta[rad]$ として次のように定義されます．

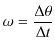
定義9.1(角速度)   $ \omega=\dfrac{\Delta\theta}{\Delta t}$

この定義によると，回転角 $ \Delta\theta[rad]$ は $ \Delta\theta=\omega\Delta t[rad]$ なので，円周に沿っての道のり $ s[m]$ は $ s=r\Delta\theta=r\omega\Delta t[m]$ になります．よって，物体の速さ $ v[m/s]$ は，

$\displaystyle v$ $\displaystyle =\dfrac{\Delta s}{\Delta t}$    
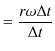  $\displaystyle =\dfrac{r\omega\Delta t}{\Delta t}$    
  $\displaystyle =r\omega$    

です．ただし，速度の向きは円の接線方向です．図のように，速度の変化量 $ \Delta\vec{v}[m/s]$ は，緑色の矢印で表されますが， $ \Delta t[s]$ が微小のとき，速度の変化量の大きさ $ \vert\Delta\vec{v}[m/s]\vert$ は円弧の長さ $ v\Delta\theta=v\omega\Delta t[m]$ に近似されます．故に，加速度の大きさ $ a[m/s^{2}]$ は，

$\displaystyle a$ $\displaystyle =\dfrac{\vert\Delta\vec{v}\vert}{\Delta t}$    
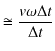  $\displaystyle \cong\dfrac{v\omega\Delta t}{\Delta t}$    
  $\displaystyle =v\omega$    

ですから，

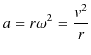
$\displaystyle a=r\omega^{2}=\dfrac{v^{2}}{r}$

となります．また，図からわかるように， $ \Delta t[s]$ を $ 0[s]$ に近づける極限で， $ \Delta\vec{v}[m/s]$ の向きと速度ベクトルの向きは垂直になりますので，速度の変化量 $ \Delta\vec{v}[m/s]$ の向きと一致している加速度の向きは，円の中心方向になることが理解されます．

　等速円運動の加速度大きさと向きを求めるには，$ x$ 座標と $ y$ 座標をとって考えることもできます．$ t=0[s]$ での物体の位置を， $ (x,y)=(r,0)$ とすると，図より，

$\displaystyle x$ $\displaystyle =r\cos\omega t$    
$\displaystyle y$ $\displaystyle =r\sin\omega t$    

と表せますが，これらの式を時間で微分していき，速度，加速度を求めます．速度の $ x$ 成分と $ y$ 成分は，

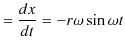$\displaystyle v_{x}$ $\displaystyle =\dfrac{dx}{dt}=-r\omega\sin\omega t$    
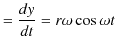$\displaystyle v_{y}$ $\displaystyle =\dfrac{dy}{dt}=r\omega\cos\omega t$    

です．よって，加速度の $ x$ 成分と $ y$ 成分は，

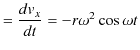$\displaystyle a_{x}$ $\displaystyle =\dfrac{dv_{x}}{dt}=-r\omega^{2}\cos\omega t$    
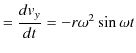$\displaystyle a_{y}$ $\displaystyle =\dfrac{dv_{y}}{dt}=-r\omega^{2}\sin\omega t$    

となります．これらの式より，加速度の大きさ $ a[m/s^{2}]$ は，

$\displaystyle a$ $\displaystyle =\sqrt{a_{x}^{2}+a_{y}^{2}}$    
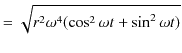  $\displaystyle =\sqrt{r^{2}\omega^{4}(\cos^{2}\omega t+\sin^{2}\omega t)}$    
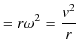  $\displaystyle =r\omega^{2}=\dfrac{v^{2}}{r}$    

となることが確認されます．また，

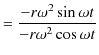$\displaystyle \dfrac{a_{y}}{a_{x}}$ $\displaystyle =\dfrac{-r\omega^{2}\sin\omega t}{-r\omega^{2}\cos\omega t}$    
  $\displaystyle =\tan\omega t$    
  $\displaystyle =\tan\theta$    

となります．故に，加速度の向きは円の中心方向になることが理解されます．この円の中心方向への加速度のことを向心加速度と言います．

 

9.2 向心力と力学的エネルギー保存則・角運動量保存則

等速円運動では，円の中心方向に向心加速度が生じていますが，ここで，運動方程式より，加速度の原因となる力が円の中心方向にはたらいていることになります．この力のことを向心力と言います．向心力の例を挙げておきましょう．天井から糸で下げられた円錐振り子の場合は，糸の張力の水平成分が向心力の役目をします．回転する円盤の上の物体については，静止摩擦力が向心力の役目をします．惑星の公転運動では重力（万有引力）が向心力の役目をします．磁場中で円運動する荷電粒子の場合は，ローレンツ力が向心力の役目をします．原子内での電子の円運動ではクーロン力が向心力の役目をします．

　等速円運動の場合，運動の向きである速度の向きは円の接線方向です．それに対して向心力は円の中心方向にはたらきます．したがって，運動の向きと力の向きは垂直の関係にあり，仕事は $ 0[J]$ になります．そこで，力学的エネルギー保存則が成立するのですが，確かに，速さが一定で，運動エネルギーは変化していないことはすぐにわかります．

　また，向心力は円の中心方向にはたらくといいましたが，円の中心は回転軸です．従って，モーメントは $ 0[N\cdot m]$ なので，角運動量保存則も成立します．物体が $ xy$ 平面上で等速円運動しているとき，確かに，角運動量の向きは $ z$ 軸方向で変わらず，その大きさも変化しないことが理解できます．