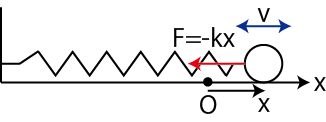
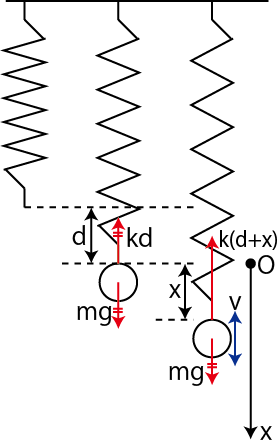
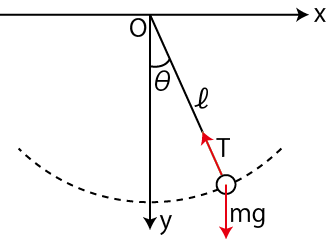
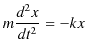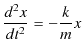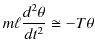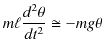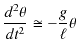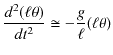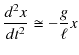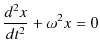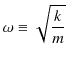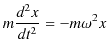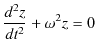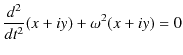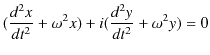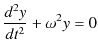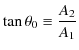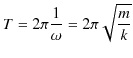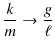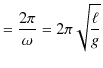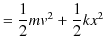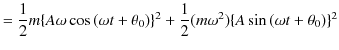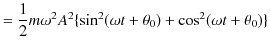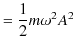次の例として,ばねを鉛直方向に吊るし,上端を固定し下端に物体を取り付け,振動させる場合を考えましょう.このときの系を鉛直ばね振り子と言います.この場合,物体に働く力 ![]() は
は ![]() 軸を下向きにとって,次のようになります.
軸を下向きにとって,次のようになります.
ここで,![]() は重力,
は重力,![]() は自然長からつりあいの位置までの長さ,
は自然長からつりあいの位置までの長さ,![]() はつりあいの位置からの物体の変位です.また,式の変形にはつりあいの位置において,
はつりあいの位置からの物体の変位です.また,式の変形にはつりあいの位置において,![]() が成立することを用いました.この力
が成立することを用いました.この力 ![]() は復元力であり,水平ばね振り子の場合と同じ式になっています.従って,鉛直ばね振り子の場合も微分方程式は(10.1)式になり,調和振動子であることが理解されます.
は復元力であり,水平ばね振り子の場合と同じ式になっています.従って,鉛直ばね振り子の場合も微分方程式は(10.1)式になり,調和振動子であることが理解されます.