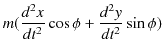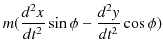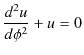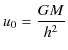Chapter11 例5（惑星の運動）

11.1 惑星の運動

惑星の運動についての研究は，力学成立の歴史に深い繋がりがあります．1576年，デンマークのティコ・ブラーエは天体の観測を開始し，精密なデータを残しました．その後，ティコ・ブラーエの弟子のケプラーは，観測データをもとに試行錯誤を繰り返した後，1609年にケプラーの第一，第二法則を発見しました．さらに，1619年にケプラーの第三法則を発見しています．ケプラーの三法則を踏み台にして，ニュートンは万有引力の法則を発見し，ニュートンの三法則とあわせて力学を創り上げました．1687年には，力学の集大成である有名なプリンキピアを出版しています．ここに，物理法則発見の典型的なパターンがあることに注目して下さい．実験結果からケプラーの三法則という規則性を見出し，さらにニュートンの力学へと本質的な発展を遂げています．一旦，ニュートン力学が成立すると，逆にニュートン力学からケプラーの三法則を導けることも確認できます．

　歴史は繰り返すといいますが，19世紀から20世紀初頭にかけての量子力学の成立も，同様な発展をしているのは興味深いことです．すなわち，まず1890年，リュードベリは実験結果から帰納して，水素原子のスペクトルの一般公式を発表しました．その公式を解明するものとして，1913年にボーアは水素原子構造理論を提案しました．このあたりの理論は前期量子論といいます．そして本質を捉えた真の理論として，1925年のハイゼンベルクによる量子力学（行列による表示），1926年のシュレディンガーによる量子力学（波動による表示）が打ち立てられました．また，完成された量子力学から水素原子のスペクトルを説明することもできます．自然法則は現象論的な法則の発見から，より深い本質的な法則の発見へと繋がっていくのです．

 

11.2 ケプラーの法則から万有引力の法則へ

ケプラーの三法則とは次のようなものです．

法則11.1(第一法則) "惑星は太陽を焦点の１つとする楕円軌道を描きます．"

法則11.2(第二法則（面積速度一定の法則）) "太陽と惑星を結ぶ直線が単位時間に掃過する面積は一定です．"

法則11.3(第三法則) "惑星が太陽の周りを回る周期 $ T[s]$ の2乗は楕円軌道の長半径 $ a[m]$ の3乗に比例します．（ $ T^{2}=ka^{3}$）"

ケプラーの法則からニュートンの万有引力の法則を導いてみましょう．まず，質量 $ m[kg]$ の惑星は楕円軌道を描いて運動していますが，簡単のため，この運動を半径 $ r[m]$ ，角速度 $ \omega[rad/s]$ の等速円運動に近似します．（ここで，第一法則と第二法則を使っています．）このとき，円の中心方向への加速度の原因となる力の役目をするものが必要ですが，それは不明です．とりあえず，この力が太陽からの引力 $ F[N]$ であるとして，その大きさを求めましょう．

$\displaystyle F$ $\displaystyle =mr\omega^{2}$    
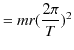  $\displaystyle =mr(\dfrac{2\pi}{T})^{2}$    
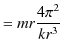  $\displaystyle =mr\dfrac{4\pi^{2}}{kr^{3}}$    

最後の変形には第三法則を用いました．式の変形を続けて，

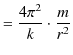$\displaystyle F$ $\displaystyle =\dfrac{4\pi^{2}}{k}\cdot\dfrac{m}{r^{2}}$    
  $\displaystyle =C\dfrac{m}{r^{2}}$    

となります．ただし，

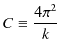
$\displaystyle C\equiv\dfrac{4\pi^{2}}{k}$

と，おきました．ここで，作用・反作用の法則より，惑星が太陽に引かれているならば，太陽も惑星に引かれているはずです．したがって，$ F[N]$ は太陽の質量 $ M[kg]$ にも比例するはずです．よって，

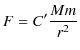
$\displaystyle F=C'\dfrac{Mm}{r^{2}}$

の形の引力が惑星と太陽の間に働いています．ここで，ニュートンは一つの飛躍をします．太陽と惑星の間に働いている引力は，地球上の物体と地球が引き合っている力と同じものではないかと思い付いたのです．さらに，質量があるもの全て，万物には引力が働くものとし，万有引力という考えに到達したのです．有名なリンゴの木のエピソードは真偽の程は明らかではありませんが，リンゴが木から落ちるのを見たニュートンが，リンゴと地球が引き合っているということを思いつき，それが万物が引き合っている力の一つであることを見抜いたと言われます．ニュートンは天上の法則と地上の法則を統一したのです．万有引力の法則を再掲しておきます．

$\displaystyle F=G\dfrac{m_{1}m_{2}}{r^{2}}$ (11.1)

 

11.3 ニュートン力学からケプラーの法則へ

一旦，万有引力の法則とニュートンの三法則からなるニュートン力学が成立すると，それからケプラーの法則が導かれることを確認しましょう．まず準備として，中心力が働く場合の2次元の運動を極座標で取り扱っておきます．座標軸 $ (x,y)$ を平面極座標 $ (r,\phi)$ で表します．

$\displaystyle x$ $\displaystyle =r\cos\phi$    
$\displaystyle y$ $\displaystyle =r\sin\phi$    

$ x$ と $ y$ を時間で微分します．

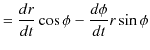$\displaystyle \dfrac{dx}{dt}$ $\displaystyle =\dfrac{dr}{dt}\cos\phi-\dfrac{d\phi}{dt}r\sin\phi$    
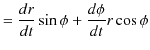$\displaystyle \dfrac{dy}{dt}$ $\displaystyle =\dfrac{dr}{dt}\sin\phi+\dfrac{d\phi}{dt}r\cos\phi$    

さらに，もう一回時間で微分します．

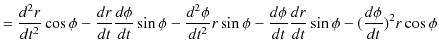$\displaystyle \dfrac{d^{2}x}{dt^{2}}$ $\displaystyle =\dfrac{d^{2}r}{dt^{2}}\cos\phi-\dfrac{dr}{dt}\dfrac{d\phi}{dt}\s... ...in\phi-\dfrac{d\phi}{dt}\dfrac{dr}{dt}\sin\phi-(\dfrac{d\phi}{dt})^{2}r\cos\phi$    
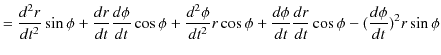$\displaystyle \dfrac{d^{2}y}{dt^{2}}$ $\displaystyle =\dfrac{d^{2}r}{dt^{2}}\sin\phi+\dfrac{dr}{dt}\dfrac{d\phi}{dt}\c... ...os\phi+\dfrac{d\phi}{dt}\dfrac{dr}{dt}\cos\phi-(\dfrac{d\phi}{dt})^{2}r\sin\phi$    

形を整えると次のようになります．

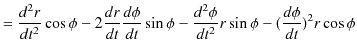$\displaystyle \dfrac{d^{2}x}{dt^{2}}$ $\displaystyle =\dfrac{d^{2}r}{dt^{2}}\cos\phi-2\dfrac{dr}{dt}\dfrac{d\phi}{dt}\sin\phi-\dfrac{d^{2}\phi}{dt^{2}}r\sin\phi-(\dfrac{d\phi}{dt})^{2}r\cos\phi$    
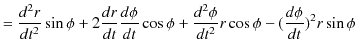$\displaystyle \dfrac{d^{2}y}{dt^{2}}$ $\displaystyle =\dfrac{d^{2}r}{dt^{2}}\sin\phi+2\dfrac{dr}{dt}\dfrac{d\phi}{dt}\cos\phi+\dfrac{d^{2}\phi}{dt^{2}}r\cos\phi-(\dfrac{d\phi}{dt})^{2}r\sin\phi$    

動径方向に働く中心力の大きさを $ f(r)$ とすると，運動方程式の $ x$ 成分と $ y$ 成分は次のようになります．

$\displaystyle m\dfrac{d^{2}x}{dt^{2}}$ $\displaystyle =f(r)\cos\phi$    
$\displaystyle m\dfrac{d^{2}y}{dt^{2}}$ $\displaystyle =f(r)\sin\phi$    

この２つの式から，次のように変形されます．

$\displaystyle m(\dfrac{d^{2}x}{dt^{2}}\cos\phi+\dfrac{d^{2}y}{dt^{2}}\sin\phi)$ $\displaystyle =f(r)$ (11.2)
$\displaystyle m(\dfrac{d^{2}x}{dt^{2}}\sin\phi-\dfrac{d^{2}y}{dt^{2}}\cos\phi)$ $\displaystyle =0$ (11.3)

(11.2)式は次のようになります．

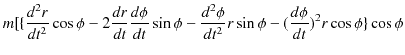  $\displaystyle m[\{\dfrac{d^{2}r}{dt^{2}}\cos\phi-2\dfrac{dr}{dt}\dfrac{d\phi}{d... ...i-\dfrac{d^{2}\phi}{dt^{2}}r\sin\phi-(\dfrac{d\phi}{dt})^{2}r\cos\phi\}\cos\phi$    
  $\displaystyle \,\,\,+\{\dfrac{d^{2}r}{dt^{2}}\sin\phi+2\dfrac{dr}{dt}\dfrac{d\p... ...ac{d^{2}\phi}{dt^{2}}r\cos\phi-(\dfrac{d\phi}{dt})^{2}r\sin\phi\}\sin\phi]=f(r)$    
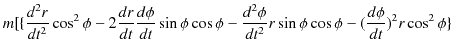% latex2html id marker 1307 $\displaystyle \therefore$ $\displaystyle m[\{\dfrac{d^{2}r}{dt^{2}}\cos^{2}\phi-2\dfrac{dr}{dt}\dfrac{d\ph... ...c{d^{2}\phi}{dt^{2}}r\sin⁡\phi\cos\phi-(\dfrac{d\phi}{dt})^{2}r\cos^{2}\phi\}$    
  $\displaystyle \,\,\,+\{\dfrac{d^{2}r}{dt^{2}}\sin^{2}\phi+2\dfrac{dr}{dt}\dfrac... ...^{2}\phi}{dt^{2}}r\sin\phi\cos\phi-(\dfrac{d\phi}{dt})^{2}r\sin^{2}\phi\}]=f(r)$    
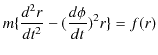% latex2html id marker 1310 $\displaystyle \therefore$ $\displaystyle m\{\dfrac{d^{2}r}{dt^{2}}-(\dfrac{d\phi}{dt})^{2}r\}=f(r)$    

(11.3)式を変形します．

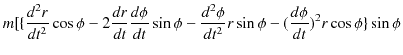  $\displaystyle m[\{\dfrac{d^{2}r}{dt^{2}}\cos\phi-2\dfrac{dr}{dt}\dfrac{d\phi}{d... ...i-\dfrac{d^{2}\phi}{dt^{2}}r\sin\phi-(\dfrac{d\phi}{dt})^{2}r\cos\phi\}\sin\phi$    
  $\displaystyle \,\,\,-\{\dfrac{d^{2}r}{dt^{2}}\sin\phi+2\dfrac{dr}{dt}\dfrac{d\p... ...dfrac{d^{2}\phi}{dt^{2}}r\cos\phi-(\dfrac{d\phi}{dt})^{2}r\sin\phi\}\cos\phi]=0$    
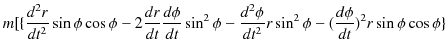% latex2html id marker 1314 $\displaystyle \therefore$ $\displaystyle m[\{\dfrac{d^{2}r}{dt^{2}}\sin\phi\cos\phi-2\dfrac{dr}{dt}\dfrac{... ...frac{d^{2}\phi}{dt^{2}}r\sin^{2}\phi-(\dfrac{d\phi}{dt})^{2}r\sin\phi\cos\phi\}$    
  $\displaystyle \,\,\,-\{\dfrac{d^{2}r}{dt^{2}}\sin\phi\cos⁡\phi+2\dfrac{dr}{dt... ...c{d^{2}\phi}{dt^{2}}r\cos^{2}\phi-(\dfrac{d\phi}{dt})^{2}r\sin\phi\cos\phi\}]=0$    
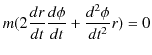% latex2html id marker 1317 $\displaystyle \therefore$ $\displaystyle m(2\dfrac{dr}{dt}\dfrac{d\phi}{dt}+\dfrac{d^{2}\phi}{dt^{2}}r)=0$    

惑星の運動の場合，中心力 $ f(r)$ として万有引力が働くので，微分方程式は，それぞれ次のようになります．

  $\displaystyle m\{\dfrac{d^{2}r}{dt^{2}}-(\dfrac{d\phi}{dt})^{2}r\}=-G\dfrac{Mm}{r^{2}}$ (11.4)
  $\displaystyle m(2\dfrac{dr}{dt}\dfrac{d\phi}{dt}+\dfrac{d^{2}\phi}{dt^{2}}r)=0$ (11.5)

ここで，(11.5)式は次のように変形されます．

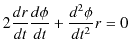  $\displaystyle 2\dfrac{dr}{dt}\dfrac{d\phi}{dt}+\dfrac{d^{2}\phi}{dt^{2}}r=0$    
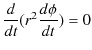% latex2html id marker 1324 $\displaystyle \therefore$ $\displaystyle \dfrac{d}{dt}(r^{2}\dfrac{d\phi}{dt})=0$    

時間で積分すると，次の式が成立します．

$\displaystyle r^{2}\dfrac{d\phi}{dt}=h\,(const)$ (11.6)

ここで，時間 $ dt[s]$ の間に惑星の動径が掃過する面積は，

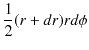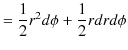$\displaystyle \dfrac{1}{2}(r+dr)rd\phi$ $\displaystyle =\dfrac{1}{2}r^{2}d\phi+\dfrac{1}{2}rdrd\phi$    
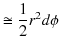  $\displaystyle \cong\dfrac{1}{2}r^{2}d\phi$    

となります．（図を参照して下さい．）

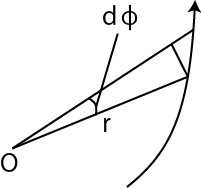
面積速度1

Figure11.1: 面積速度1

従って，惑星の動径が単位時間に掃過する面積（面積速度）は，

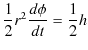
$\displaystyle \dfrac{1}{2}r^{2}\dfrac{d\phi}{dt}=\dfrac{1}{2}h$

となり，これは(11.6)式より一定です．すなわち，ケプラーの第二法則が導出されました．

　ここで，ケプラーの第二法則は，角運動量保存則から導出されることも見ておきましょう．

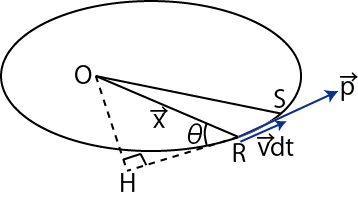
面積速度2

Figure11.2: 面積速度2

面積速度の大きさは，下図の惑星が微小時間 $ dt[s]$ の間に掃過する3角形 $ ORS$ の面積を $ dt[s]$ で割り，次のように求められます．

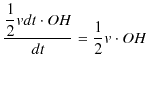
$\displaystyle \dfrac{\dfrac{1}{2}vdt\cdot OH}{dt}=\dfrac{1}{2}v\cdot OH$

一方，惑星の角運動量の大きさは，

$\displaystyle \vert\vec{L}\vert$ $\displaystyle =\vert\vec{x}\times\vec{p}\vert$    
  $\displaystyle =\vert\vec{x}\vert p\sin\theta$    
  $\displaystyle =p\cdot OH$    
  $\displaystyle =mv\cdot OH$    

となりますので，面積速度の大きさは，

$\displaystyle \dfrac{1}{2m}\vert\vec{L}\vert$

と表せます．したがって，中心力を受けて運動する物体の角運動量は保存することから，惑星の面積速度が一定になることが証明されました．

　次に，(11.4)式，

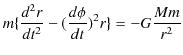
$\displaystyle m\{\dfrac{d^{2}r}{dt^{2}}-(\dfrac{d\phi}{dt})^{2}r\}=-G\dfrac{Mm}{r^{2}}$

を変形します．

$\displaystyle \dfrac{d^{2}r}{dt^{2}}-(\dfrac{d\phi}{dt})^{2}r=-G\dfrac{M}{r^{2}}$ (11.7)

となりますが，ここで，$ r[m]$ は $ \phi[rad]$ を通して時間の関数なので，

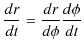
$\displaystyle \dfrac{dr}{dt}=\dfrac{dr}{d\phi}\dfrac{d\phi}{dt}$

が成立します．ここで，(11.6)式，

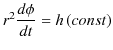
$\displaystyle r^{2}\dfrac{d\phi}{dt}=h\,(const)$

より，

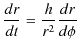
$\displaystyle \dfrac{dr}{dt}=\dfrac{h}{r^{2}}\dfrac{dr}{d\phi}$

となります．さらに，

$\displaystyle u\equiv\dfrac{1}{r}$

とおくと，

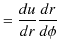$\displaystyle \dfrac{du}{d\phi}$ $\displaystyle =\dfrac{du}{dr}\dfrac{dr}{d\phi}$    
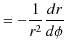  $\displaystyle =-\dfrac{1}{r^{2}}\dfrac{dr}{d\phi}$    

ですから，

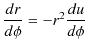
$\displaystyle \dfrac{dr}{d\phi}=-r^{2}\dfrac{du}{d\phi}$

となります．したがって，

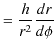$\displaystyle \dfrac{dr}{dt}$ $\displaystyle =\dfrac{h}{r^{2}}\dfrac{dr}{d\phi}$    
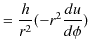  $\displaystyle =\dfrac{h}{r^{2}}(-r^{2}\dfrac{du}{d\phi})$    
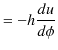  $\displaystyle =-h\dfrac{du}{d\phi}$    

ですから，

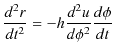
$\displaystyle \dfrac{d^{2}r}{dt^{2}}=-h\dfrac{d^{2}u}{d\phi^{2}}\dfrac{d\phi}{dt}$

となります．ここで，(11.6)式，

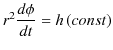
$\displaystyle r^{2}\dfrac{d\phi}{dt}=h\,(const)$

を使って，

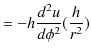$\displaystyle \dfrac{d^{2}r}{dt^{2}}$ $\displaystyle =-h\dfrac{d^{2}u}{d\phi^{2}}(\dfrac{h}{r^{2}})$    
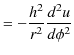  $\displaystyle =-\dfrac{h^{2}}{r^{2}}\dfrac{d^{2}u}{d\phi^{2}}$    

となります．このとき，(11.7)式は(11.6)式をもう一度使って，次のように計算されます．

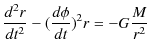  $\displaystyle \dfrac{d^{2}r}{dt^{2}}-(\dfrac{d\phi}{dt})^{2}r=-G\dfrac{M}{r^{2}}$    
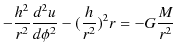% latex2html id marker 1391 $\displaystyle \therefore$ $\displaystyle -\dfrac{h^{2}}{r^{2}}\dfrac{d^{2}u}{d\phi^{2}}-(\dfrac{h}{r^{2}})^{2}r=-G\dfrac{M}{r^{2}}$    
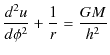% latex2html id marker 1393 $\displaystyle \therefore$ $\displaystyle \dfrac{d^{2}u}{d\phi^{2}}+\dfrac{1}{r}=\dfrac{GM}{h^{2}}$    

したがって，

$\displaystyle \dfrac{d^{2}u}{d\phi^{2}}+u=\dfrac{GM}{h^{2}}$ (11.8)

となります．(11.8)式は定数係数の２階線形非同次部分方程式になっています．解法は右辺を0とおいた同次方程式の解と(11.8)式の特解の和で求めることができます．同次方程式は，

$\displaystyle \dfrac{d^{2}u}{d\phi^{2}}+u=0$ (11.9)

となりますが，この式は "例4（調和振動子）" のChapterで取り扱った調和振動子の微分方程式，

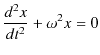
$\displaystyle \dfrac{d^{2}x}{dt^{2}}+\omega^{2}x=0$

と同形になっています．この方程式の解は，

$\displaystyle x=A_{1}\sin\omega t+A_{2}\cos\omega t$

となっていました．この解において，$ x\to u$， $ \omega\to1$，$ t\to\phi$ と置き換え，同次方程式(11.9)式の解は，

$\displaystyle u=A_{1}\sin\phi+A_{2}\cos\phi$ (11.10)

となります．また，(11.8)式，

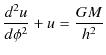
$\displaystyle \dfrac{d^{2}u}{d\phi^{2}}+u=\dfrac{GM}{h^{2}}$

の特解の一つとして，

$\displaystyle u_{0}=\dfrac{GM}{h^{2}}$ (11.11)

があることが，直ちにわかります．従って，(11.8)式の解は，(11.10)式と(11.11)式の和になり，

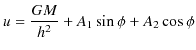
$\displaystyle u=\dfrac{GM}{h^{2}}+A_{1}\sin\phi+A_{2}\cos\phi$

ここで，簡単のため，$ \phi=0$ において，惑星が太陽から最も遠くに位置する，つまり，$ r[m]$ が最大値をとるものとします．このとき，$ u$ は最小値をとりますので，

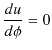
$\displaystyle \dfrac{du}{d\phi}=0$

の条件が成立します．よって，

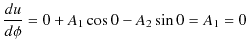
$\displaystyle \dfrac{du}{d\phi}=0+A_{1}\cos⁡0-A_{2}\sin⁡0=A_{1}=0$

になりますので，(11.8)式の解は，

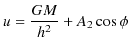  $\displaystyle u=\dfrac{GM}{h^{2}}+A_{2}\cos\phi$    
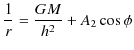% latex2html id marker 1428 $\displaystyle \therefore$ $\displaystyle \dfrac{1}{r}=\dfrac{GM}{h^{2}}+A_{2}\cos\phi$    
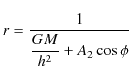% latex2html id marker 1430 $\displaystyle \therefore$ $\displaystyle r=\dfrac{1}{\dfrac{GM}{h^{2}}+A_{2}\cos\phi}$    
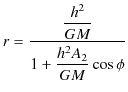% latex2html id marker 1432 $\displaystyle \therefore$ $\displaystyle r=\dfrac{\dfrac{h^{2}}{GM}}{1+\dfrac{h^{2}A_{2}}{GM}\cos\phi}$    

となりますが，

$\displaystyle \ell$ $\displaystyle \equiv\dfrac{h^{2}}{GM}$    
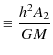$\displaystyle \varepsilon$ $\displaystyle \equiv\dfrac{h^{2}A_{2}}{GM}$    

とおくと，軌道の方程式は，

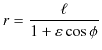
$\displaystyle r=\dfrac{\ell}{1+\varepsilon\cos\phi}$

となります．この式は，原点を焦点とする楕円（ $ \varepsilon<1$），放物線（ $ \varepsilon=1$），双曲線（ $ \varepsilon>1$）を表しています．ケプラーの第一法則が導かれました．

　楕円の半長軸を $ a[m]$，半短軸を $ b[m]$ とすれば，

$\displaystyle b^{2}=\ell a$

の関係が成立します．したがって，楕円の面積 $ S[m^{2}]$ は，

$\displaystyle S$ $\displaystyle =\pi ab$    
  $\displaystyle =\pi\sqrt{\ell a^{3}}$    
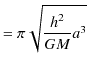  $\displaystyle =\pi\sqrt{\dfrac{h^{2}}{GM}a^{3}}$    
  $\displaystyle =\dfrac{\pi}{\sqrt{GM}}ha^{\frac{3}{2}}$    

となります．周期 $ T[s]$ は楕円の面積 $ S[m^{2}]$ を面積速度 $ h/2[m^{2}/s]$ で割れば求められます．

$\displaystyle T$ $\displaystyle =\dfrac{S}{h/2}$    
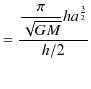  $\displaystyle =\dfrac{\dfrac{\pi}{\sqrt{GM}}ha^{\frac{3}{2}}}{h/2}$    
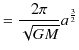  $\displaystyle =\dfrac{2\pi}{\sqrt{GM}}a^{\frac{3}{2}}$    
  $\displaystyle \propto a^{\frac{3}{2}}$    

故に，次式が成立します．

$\displaystyle T^{2}=ka^{3}$

ただし，$ k$ は比例定数です．ケプラーの第三法則が導かれました．ケプラーの三法則は全て，ニュートン力学から導出することができたのです．