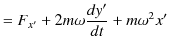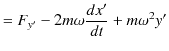J Simplicity 相対運動

Chapter12 相対運動

12.1 ガリレイ変換

慣性の法則が成立する座標系を慣性系といいます．慣性系においては運動の法則（運動方程式）が成立します．ここで，一つの慣性系に対して等速直線運動をする座標系の物理を考えましょう．例えば，地面の水平方向は良い近似で慣性系ですが，その上で等速直線運動する列車を想定します．まず，列車の中で列車に対して静止している物体を考えます．このとき，地面にいる観測者に対しては，動いている物体は等速直線運動を続けるという意味で慣性の法則が成立しています．（図 "慣性系1" を参照して下さい．）

慣性系1

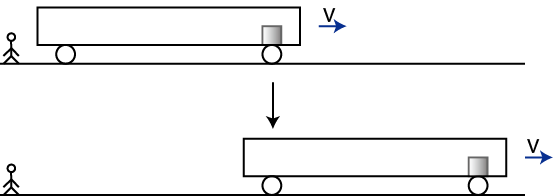
Figure12.1: 慣性系1

列車にいる観測者に対しては，静止している物体は静止を続けるという意味で慣性の法則が成立しています．（図 "慣性系2" を参照して下さい．）

慣性系2

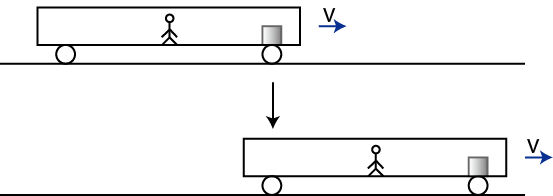
Figure12.2: 慣性系2

もし，列車の中の床がなめらかで摩擦が無視できる場合，列車の中の物体が地面に対して静止し，列車に対して後ろ向きに等速直線運動をするときも，両座標系において慣性の法則が成立しています．このことは，地面にいる観測者に対しては，静止している物体は静止を続けるという意味において言えることです．（図 "慣性系3"" を参照して下さい．）

慣性系3

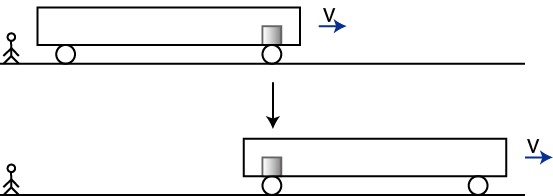
Figure12.3: 慣性系3

列車にいる観測者に対しては，動いている物体は等速直線運動を続けるという意味において，慣性の法則が成立しています．（図 "慣性系4" を参照して下さい．）

慣性系4

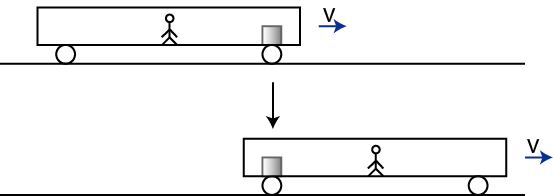
Figure12.4: 慣性系4

このように，

原理12.1(ガリレイの相対性原理) "1つの慣性系に対して等速直線運動をしている座標系はやはり慣性系です．"

という原理が成立します．これをガリレイの相対性原理といいます．

　上記の記述をやや一般的にします．慣性系に対して，方向に相対速度（一定）で動いている座標系を考えます．慣性系について，運動方程式，

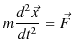
$\displaystyle m\dfrac{d^{2}\vec{x}}{dt^{2}}=\vec{F}\,$

が成立します．また，簡単のため，図のように，軸と軸は重なっていて，の座標系はその方向に等速直線運動しているものとします．

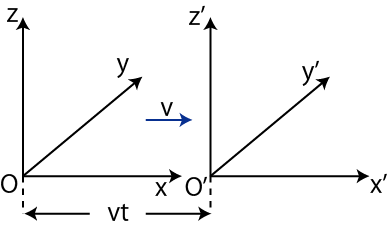
ガリレイ変換

Figure12.5: ガリレイ変換

このときの両座標系の間の関係式は，次のようになります．

$\displaystyle x'$	$\displaystyle =x-vt$	(12.1)
$\displaystyle y'$	$\displaystyle =y$	(12.2)
$\displaystyle z'$	$\displaystyle =z$	(12.3)

(12.1)式～(12.3)式で表される座標変換をガリレイ変換といいます．ガリレイ変換に対して，各座標を時間で微分していくと，次のようになります．

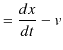$\displaystyle \dfrac{dx'}{dt}$	$\displaystyle =\dfrac{dx}{dt}-v$
$\displaystyle \dfrac{dy'}{dt}$	$\displaystyle =\dfrac{dy}{dt}$
$\displaystyle \dfrac{dz'}{dt}$	$\displaystyle =\dfrac{dz}{dt}$

故に，

$\displaystyle \dfrac{d^{2}x'}{dt^{2}}$	$\displaystyle =\dfrac{d^{2}x}{dt^{2}}$
$\displaystyle \dfrac{d^{2}y'}{dt^{2}}$	$\displaystyle =\dfrac{d^{2}y}{dt^{2}}$
$\displaystyle \dfrac{d^{2}z'}{dt^{2}}$	$\displaystyle =\dfrac{d^{2}z}{dt^{2}}$

となります．したがって，座標系についても，運動方程式，

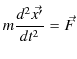
$\displaystyle m\dfrac{d^{2}\vec{x'}}{dt^{2}}=\vec{F}$

が成立します．運動方程式が成立する座標系は慣性系ですから，座標系も慣性系になります．つまり，ガリレイの相対性原理が成り立つことになります．

　ニュートン力学における相対性については，上記のようにガリレイ変換を考えますが，実は特殊相対性理論においては，ローレンツ変換という座標変換を取り扱うことになります．詳しくは ``相対性理論'' のReportをご覧ください．

12.2 並進運動

一つの慣性系に対して等加速度直線運動する座標系の物理を考えましょう．例えば，水平方向がよい近似で慣性系である地面の上で，等加速度直線運動する列車を想定します．列車の中に物体を置き，ばねを取り付けておきます．列車が加速運動するとき，ばねは伸びることが観測されます．この状況について，地面にいる観測者にとっての物理と，列車に乗り込んだ観測者にとっての物理について考えてみます．地面にいる観測者は，ばねの弾性力が原因で物体が等加速度直線運動すると観測します．（図 "慣性力1" を参照して下さい．）そのとき，成立する運動方程式は物体の質量を，列車の加速度を $a[m/s^{2}]$ として，次式になります．

$\displaystyle ma=F$

(12.4)

慣性力1

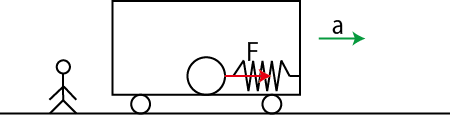
Figure12.6: 慣性力1

一方，列車に乗り込んだ観測者には，物体は静止して見えます．しかし，この場合もばねの弾性力は働いており，このままでは力はつりあうことができません．そこで，列車の加速度の向きと逆向きに，見かけの力として慣性力といわれるものを導入することにしましょう．（図 "慣性力2" を見て下さい．）この慣性力をとすると，成立するつりあいの式は，

$\displaystyle F'=F$

(12.5)

となります．

慣性力2

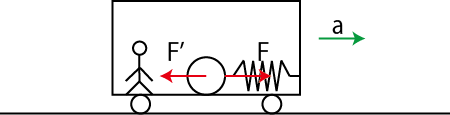
Figure12.7: 慣性力2

(12.4)式と(12.5)式から（向きまで考慮して），慣性力は，

$\displaystyle F'=-ma$

と表されます．

　上記の物理を一般的に取り扱ってみましょう．慣性系に対して，加速運動している座標系をとります．座標系が回転しておらず，慣性系と座標系の座標軸が平行である場合を考えます．

並進運動

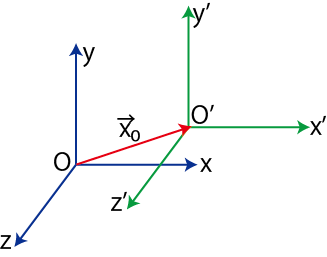
Figure12.8: 並進運動

このとき，

$\displaystyle x$	$\displaystyle =x_{0}+x'$
$\displaystyle y$	$\displaystyle =y_{0}+y'$
$\displaystyle z$	$\displaystyle =z_{0}+z'$

すなわち，

$\displaystyle \vec{x}=\vec{x}_{0}+\vec{x'}\,$

が成立します．慣性系に対しては，運動方程式，

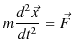
$\displaystyle m\dfrac{d^{2}\vec{x}}{dt^{2}}=\vec{F}\,$

が成立します．ここで，

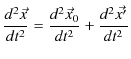
$\displaystyle \dfrac{d^{2}\vec{x}}{dt^{2}}=\dfrac{d^{2}\vec{x}_{0}}{dt^{2}}+\dfrac{d^{2}\vec{x'}}{dt^{2}}$

が成り立つので，慣性系(x,y,z)に対する運動方程式は，次のように変形されます．

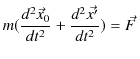	$\displaystyle m(\dfrac{d^{2}\vec{x}_{0}}{dt^{2}}+\dfrac{d^{2}\vec{x'}}{dt^{2}})=\vec{F}\,$
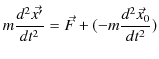$% latex2html id marker 1292 $\displaystyle \therefore$$	$\displaystyle m\dfrac{d^{2}\vec{x'}}{dt^{2}}=\vec{F}+(-m\dfrac{d^{2}\vec{x}_{0}}{dt^{2}})$

ここで，

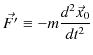
$\displaystyle \vec{F'}\equiv-m\dfrac{d^{2}\vec{x}_{0}}{dt^{2}}$

とおくと，

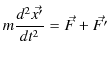
$\displaystyle m\dfrac{d^{2}\vec{x'}}{dt^{2}}=\vec{F}+\vec{F'}$

となります． $\vec{F'}[N]$ は見かけの力であり，慣性力です．つまり，上式が表しているものは，

　"慣性系に対して加速運動している座標系では，慣性力が現れ，これを加えれば運動方程式が成立します．"

という内容です．

　慣性力は見かけの力として便宜上，力学に導入された経緯があります．しかし，この力が本物の重力と同等であるという等価原理を唱え，重力の幾何学化を実行したのがアインシュタインの一般相対性理論です．詳しくは "相対性理論" のReportをご覧下さい．

12.3 回転運動

一つの慣性系に対して，等速円運動する座標系の物理を考えましょう．例えば，水平方向がよい近似で慣性系である地面の上で等速円運動する円板を想定します．円板の中に物体をおき，ばねを取り付けておきます．円板が等速円運動するとき，物体も円板とともに等速円運動して，ばねは伸びることが観測されます．この状況について，地面にいる観測者にとっての物理と，円板に乗り込んだ観測者の物理について考えます．地面にいる観測者は，ばねの弾性力が向心力の役目をして，物体が等速円運動すると観測します．（図 "遠心力1" を参照して下さい．）

遠心力1

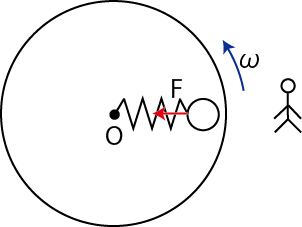
Figure12.9: 遠心力1

このとき，成立する円の中心方向への運動方程式は，円の半径を，物体の質量を，円板の角速度を $\omega[rad/s]$ として，次式であることがわかります．

$\displaystyle m\cdot r\omega^{2}=F$

(12.6)

一方，円板に乗り込んだ観測者には，物体は静止して見えます．しかし，この場合もばねの弾性力は働いており，このままでは力はつりあうことができません．そこで，円板の外向きに，見かけの力として遠心力といわれるものを導入することにしましょう．（図 "遠心力2" を参照して下さい．）

遠心力2

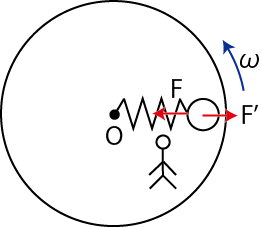
Figure12.10: 遠心力2

この遠心力をとすると，成立するつりあいの式は，

$\displaystyle F'=F$

(12.7)

となります．(12.6)式と(12.7)式から遠心力は，

$\displaystyle F'=mr\omega^{2}$

と表せます．ここで，遠心力の向きは外向きです．

　上記の物理をやや一般的に取り扱ってみましょう．慣性系に対して，回転運動している座標系をとります．ただし，簡単のため2つの座標系の原点は一致しており，回転軸は軸= 軸で，ダッシュがついた座標系が反時計回りに角速度 $\omega[rad/s]$ の2次元回転をしている場合を考えます．慣性系に対する運動方程式は，成分と成分に分けて次のようになります．

$\displaystyle m\dfrac{d^{2}x}{dt^{2}}$	$\displaystyle =F_{x}$	(12.8)
$\displaystyle m\dfrac{d^{2}y}{dt^{2}}$	$\displaystyle =F_{y}$	(12.9)

ここで，で2つの座標系が一致していたものとすると，2つの座標系は次式で表されます．（図 "回転運動1" を参照して下さい．）

$\displaystyle x$	$\displaystyle =x'\cos\omega t-y'\sin\omega t$
$\displaystyle y$	$\displaystyle =x'\sin\omega t+y'\cos\omega t$

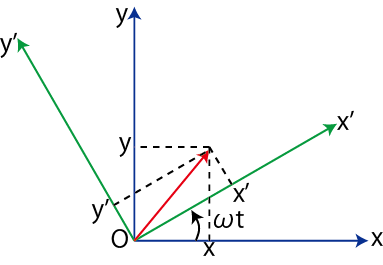
回転運動1

Figure12.11: 回転運動1

この2つの関係式を時間で微分します．

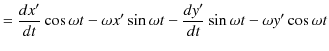$\displaystyle \dfrac{dx}{dt}$	$\displaystyle =\dfrac{dx'}{dt}\cos\omega t-\omega x'\sin\omega t-\dfrac{dy'}{dt}\sin\omega t-\omega y'\cos\omega t$
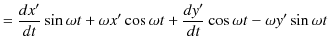$\displaystyle \dfrac{dy}{dt}$	$\displaystyle =\dfrac{dx'}{dt}\sin\omega t+\omega x'\cos\omega t+\dfrac{dy'}{dt}\cos\omega t-\omega y'\sin\omega t$

もう一度時間で微分します．

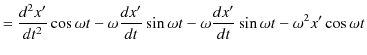$\displaystyle \dfrac{d^{2}x}{dt^{2}}$	$\displaystyle =\dfrac{d^{2}x'}{dt^{2}}\cos\omega t-\omega\dfrac{dx'}{dt}\sin\omega t-\omega\dfrac{dx'}{dt}\sin\omega t-\omega^{2}x'\cos\omega t$
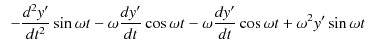	$\displaystyle \,\,\,-\dfrac{d^{2}y'}{dt^{2}}\sin\omega t-\omega\dfrac{dy'}{dt}\cos\omega t-\omega\dfrac{dy'}{dt}\cos\omega t+\omega^{2}y'\sin\omega t$
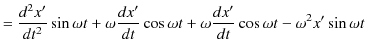$\displaystyle \dfrac{d^{2}y}{dt^{2}}$	$\displaystyle =\dfrac{d^{2}x'}{dt^{2}}\sin\omega t+\omega\dfrac{dx'}{dt}\cos\omega t+\omega\dfrac{dx'}{dt}\cos\omega t-\omega^{2}x'\sin\omega t$
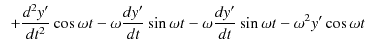	$\displaystyle \,\,\,+\dfrac{d^{2}y'}{dt^{2}}\cos\omega t-\omega\dfrac{dy'}{dt}\sin\omega t-\omega\dfrac{dy'}{dt}\sin\omega t-\omega^{2}y'\cos\omega t$

整理すると，次のようになります．

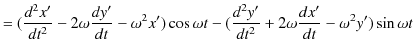$\displaystyle \dfrac{d^{2}x}{dt^{2}}$	$\displaystyle =(\dfrac{d^{2}x'}{dt^{2}}-2\omega\dfrac{dy'}{dt}-\omega^{2}x')\co... ...ega t-(\dfrac{d^{2}y'}{dt^{2}}+2\omega\dfrac{dx'}{dt}-\omega^{2}y')\sin\omega t$
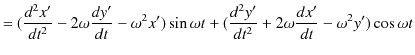$\displaystyle \dfrac{d^{2}y}{dt^{2}}$	$\displaystyle =(\dfrac{d^{2}x'}{dt^{2}}-2\omega\dfrac{dy'}{dt}-\omega^{2}x')\si... ...ega t+(\dfrac{d^{2}y'}{dt^{2}}+2\omega\dfrac{dx'}{dt}-\omega^{2}y')\cos\omega t$

一方，力については次のように変換します．（図 "回転運動2" を参照して下さい．）

$\displaystyle F_{x}$	$\displaystyle =F_{x'}\cos\omega t-F_{y'}\sin\omega t$
$\displaystyle F_{y}$	$\displaystyle =F_{x'}\sin\omega t+F_{y'}\cos\omega t$

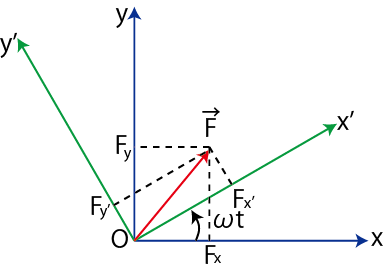
回転運動2

Figure12.12: 回転運動2

以上の議論より，慣性系における運動方程式(12.8)式と(12.9)式は，次のようになります．

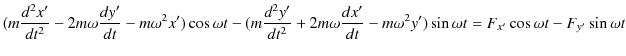	$\displaystyle (m\dfrac{d^{2}x'}{dt^{2}}-2m\omega\dfrac{dy'}{dt}-m\omega^{2}x')\... ...dfrac{dx'}{dt}-m\omega^{2}y')\sin\omega t=F_{x'}\cos\omega t-F_{y'}\sin\omega t$
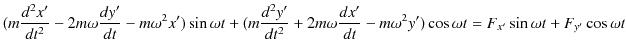	$\displaystyle (m\dfrac{d^{2}x'}{dt^{2}}-2m\omega\dfrac{dy'}{dt}-m\omega^{2}x')\... ...dfrac{dx'}{dt}-m\omega^{2}y')\cos\omega t=F_{x'}\sin\omega t+F_{y'}\cos\omega t$

これらの式の左辺と右辺を比較して，次の2式を得ます．

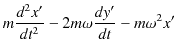$\displaystyle m\dfrac{d^{2}x'}{dt^{2}}-2m\omega\dfrac{dy'}{dt}-m\omega^{2}x'$	$\displaystyle =F_{x'}$
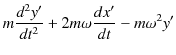$\displaystyle m\dfrac{d^{2}y'}{dt^{2}}+2m\omega\dfrac{dx'}{dt}-m\omega^{2}y'$	$\displaystyle =F_{y'}$

故に，次式が成立します．

$\displaystyle m\dfrac{d^{2}x'}{dt^{2}}$	$\displaystyle =F_{x'}+2m\omega\dfrac{dy'}{dt}+m\omega^{2}x'$	(12.10)
$\displaystyle m\dfrac{d^{2}y'}{dt^{2}}$	$\displaystyle =F_{y'}-2m\omega\dfrac{dx'}{dt}+m\omega^{2}y'$	(12.11)

(12.10)式と(12.11)式は座標系における運動方程式です．この式には見かけの力が2つ入っています．右辺第3項の $m\omega^{2}x'[N]$ と $m\omega^{2}y'[N]$ は，まとめて $\vec{F'}=m\omega^{2}\vec{x'}[N]$ と書けますが，これは遠心力です．右辺第2項の $2m\omega v_{y'}[N]$ と $-2m\omega v_{x'}[N]$ は，まとめて $-2m\vec{\omega}\times\vec{v'}[N]$ と書けますが，これはコリオリ力と呼ばれる力で，物体が座標系に対して運動している場合にのみ働く力です．

　このSectionの最後に，一つ例を挙げておきます．反時計回りに等速円運動する摩擦の円板上にある物体が，地面に対して静止し，円板に対して時計回りに等速円運動する場合を考えます．円板に乗り込んだ観測者には外向きに $F'=m\omega^{2}r'[N]$ の遠心力が働きます．しかし，円の中心方向に， $F''=2m\omega\cdot r'\omega=2m\omega^{2}r'[N]$ の大きさのコリオリ力が働き，差し引き円の中心方向に $m\omega^{2}r'[N]$ の力が働きます．この力を向心力として，物体は円板上の観測者に対して等速円運動をするのです．

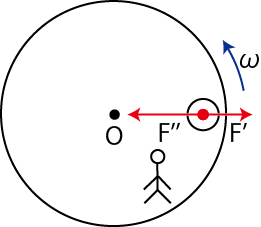
回転運動3

Figure12.13: 回転運動3