物体は鉛直下向きに運動するので,座標軸である ![]() 軸は下向きにとっています.まず,加速度は
軸は下向きにとっています.まず,加速度は
![]() ですから,
ですから,
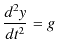
となります.これを時間 ![]() で積分していくと,
で積分していくと,
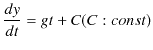 |
||
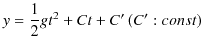 |
となります.ここで,初期条件,![]() において,
において,
![]() を代入すると,
を代入すると,
となります.さらに,初期条件,![]() において
において ![]() を代入すると,
を代入すると,
このChapterでは,物体の落下運動,いわゆる落体の運動について取り扱います.その種類としては,初速度 ![]() で鉛直下向きに運動する自由落下,初速度を鉛直下向きに与えた鉛直投げ下ろし,初速度を鉛直上向きに与えた鉛直投げ上げ,初速度を水平方向に与えた水平投射,初速度を斜め上向きに与えた斜方投射等が挙げられます.現実の落体の運動では空気の抵抗力がはたらきますが,ここでは,それを無視して考えます.
で鉛直下向きに運動する自由落下,初速度を鉛直下向きに与えた鉛直投げ下ろし,初速度を鉛直上向きに与えた鉛直投げ上げ,初速度を水平方向に与えた水平投射,初速度を斜め上向きに与えた斜方投射等が挙げられます.現実の落体の運動では空気の抵抗力がはたらきますが,ここでは,それを無視して考えます.
古代ギリシアの哲学者アリストテレスが重いものは軽いものよりも速く落下すると唱えて以来,このことはヨーロッパ社会において約2000年間信じられました.アリストテレスは理論的ではありましたが,実際に実験して検証するということをしませんでした.自由落下の実験を行ってみて,重いものも軽いものも同時に落下することを,最初に確かめたのはガリレイです.(ガリレイはピサの斜塔でその実験を行ったというエピソードが残っています.)自由落下した物体の加速度は鉛直下向きに,
で一定であり,等加速度直線運動をすることが測定されています.この
![]() のことを重力加速度といいます.加速度の原因は重力ですが,その大きさは運動方程式
のことを重力加速度といいます.加速度の原因は重力ですが,その大きさは運動方程式 ![]() において,
において,
![]() に
に
![]() を代入して,
を代入して,![]() であることが理解されます.また,力の大きさは2通りに定義されていました.つまり,
であることが理解されます.また,力の大きさは2通りに定義されていました.つまり,![]() と
と ![]() ですが,例えば,
ですが,例えば,![]() とは質量
とは質量 ![]() の物体にはたらく重力の大きさですから,
の物体にはたらく重力の大きさですから,![]() で表すと次のようになります.
で表すと次のようになります.
落体の運動では,鉛直方向の加速度が,いずれの場合も下向きに重力加速度
![]() になりますが,その理由は次のように説明されます.自由落下の実験により,そのときの加速度は鉛直下向きに,重力加速度
になりますが,その理由は次のように説明されます.自由落下の実験により,そのときの加速度は鉛直下向きに,重力加速度
![]() であることが測定されます.ここで,運動方程式
であることが測定されます.ここで,運動方程式 ![]() において,
において,
![]() に
に
![]() を代入して,加速度の原因の重力の大きさが
を代入して,加速度の原因の重力の大きさが ![]() であることがわかります.(ここまでの説明は,既に前出してあります.)この重力
であることがわかります.(ここまでの説明は,既に前出してあります.)この重力 ![]() は,自由落下に限らず,全ての落体の運動において鉛直下向きにはたらくことに注意しましょう.従って,全ての落体の運動について,鉛直方向の運動方程式は下向きを正として,
は,自由落下に限らず,全ての落体の運動において鉛直下向きにはたらくことに注意しましょう.従って,全ての落体の運動について,鉛直方向の運動方程式は下向きを正として,![]() となります.故に,全ての落体の運動について,加速度は鉛直下向きに重力加速度
となります.故に,全ての落体の運動について,加速度は鉛直下向きに重力加速度
![]() となることが理解されます.また,水平投射と斜方投射において,水平方向の運動は等速運動になりますが,その理由も述べておきます.この2つの運動において,重力は鉛直方向にはたらき,水平方向には何も力がはたらいていません.故に,水平方向は慣性の法則により等速運動を行うことが理解されます.
となることが理解されます.また,水平投射と斜方投射において,水平方向の運動は等速運動になりますが,その理由も述べておきます.この2つの運動において,重力は鉛直方向にはたらき,水平方向には何も力がはたらいていません.故に,水平方向は慣性の法則により等速運動を行うことが理解されます.
力学においては,運動を微分方程式で扱います.その際,初期条件(![]() での条件を初期条件と言います.)を与えれば運動は決定してしまいます.運動する前から,計算によってわかってしまうのです.ニュートン力学では事象は決定論的です.
での条件を初期条件と言います.)を与えれば運動は決定してしまいます.運動する前から,計算によってわかってしまうのです.ニュートン力学では事象は決定論的です.
それでは,自由落下の運動を取り扱ってみましょう.状況は図の通りです.
物体は鉛直下向きに運動するので,座標軸である ![]() 軸は下向きにとっています.まず,加速度は
軸は下向きにとっています.まず,加速度は
![]() ですから,
ですから,
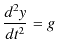
となります.これを時間 ![]() で積分していくと,
で積分していくと,
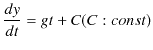 |
||
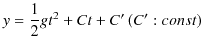 |
となります.ここで,初期条件,![]() において,
において,
![]() を代入すると,
を代入すると,
となります.さらに,初期条件,![]() において
において ![]() を代入すると,
を代入すると,
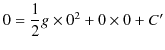 |
||
となります.したがって,
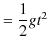 |
が成立します.
このSectionでは,鉛直方向の落体の運動を考えます.鉛直投げ下ろしと鉛直投げ上げのいずれの場合も,鉛直下向きに重力加速度
![]() で等加速度運動を行います.この2つの運動では,鉛直投げ下ろしは初速度が下向きであり,鉛直投げ上げは初速度が上向きである点のみが相違します.まず,鉛直投げ下ろしを取り扱ってみます.状況は図の通りです.
で等加速度運動を行います.この2つの運動では,鉛直投げ下ろしは初速度が下向きであり,鉛直投げ上げは初速度が上向きである点のみが相違します.まず,鉛直投げ下ろしを取り扱ってみます.状況は図の通りです.
物体は鉛直下向きに運動するので,座標軸である ![]() 軸は下向きにとってあります.まず,加速度は
軸は下向きにとってあります.まず,加速度は
![]() ですから,
ですから,
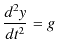
となります.これを時間 ![]() で積分していくと,
で積分していくと,
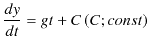 |
||
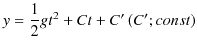 |
となります.ここで,初期条件,![]() において,
において,
![]() を代入すると,
を代入すると,
となります.さらに,初期条件,![]() において
において ![]() を代入すると,
を代入すると,
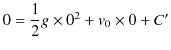 |
||
となります.したがって,
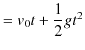 |
が成立します.
次に,鉛直投げ上げを取り扱ってみます.物体は最初,鉛直上向きに運動するので,座標軸である ![]() 軸は上向きにとってあります.まず,加速度は
軸は上向きにとってあります.まず,加速度は
![]() ですから,(
ですから,(![]() 軸を上向きにとったので,下向きの加速度は負の値になります.)
軸を上向きにとったので,下向きの加速度は負の値になります.)
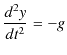
となります.これを時間 ![]() で積分していくと,
で積分していくと,
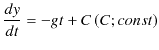 |
||
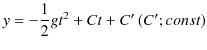 |
となります.ここで,初期条件,![]() において,
において,
![]() を代入すると,
を代入すると,
となります.さらに,初期条件,![]() において
において ![]() を代入すると,
を代入すると,
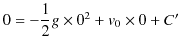 |
||
となります.したがって,
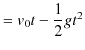 |
が成立します.
初速度
![]() で水平投射すると,物体は放物線を描いて運動しますが,水平方向(
で水平投射すると,物体は放物線を描いて運動しますが,水平方向(![]() 方向と約束します.)と鉛直方向(
方向と約束します.)と鉛直方向(![]() 方向と約束します.)に分解して取り扱います.
方向と約束します.)に分解して取り扱います.![]() 方向は等速運動を行い,
方向は等速運動を行い,![]() 方向は下向きに重力加速度
方向は下向きに重力加速度
![]() で等加速度運動をするという特徴がありました.
で等加速度運動をするという特徴がありました.
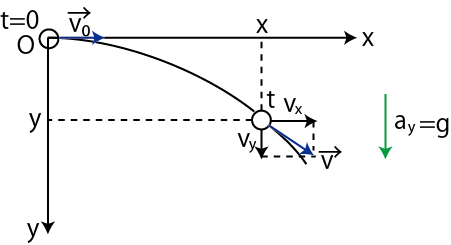
Figure8.4: 放物運動1
![]() 方向は等速運動するので,次式が成立します.
方向は等速運動するので,次式が成立します.
![]() 方向は初速度
方向は初速度 ![]() ,加速度
,加速度
![]() で等加速度運動をするので,自由落下と同じになります.したがって,次式が成立します.(自由落下の場合と同じく,
で等加速度運動をするので,自由落下と同じになります.したがって,次式が成立します.(自由落下の場合と同じく,![]() 軸は鉛直下向きにとりました.)
軸は鉛直下向きにとりました.)
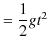 |
時間 ![]() を消去して,
を消去して,![]() と
と ![]() の関係を求めると次のようになります.
の関係を求めると次のようになります.
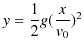 |
||
最後の関係式は,図の中の物体が描く軌跡の方程式を意味しています.
次に,初速度の大きさ
![]() ,仰角
,仰角
![]() で斜方投射する場合を考えます.物体は放物線を描いて運動しますが,水平投射と同様に,水平方向(
で斜方投射する場合を考えます.物体は放物線を描いて運動しますが,水平投射と同様に,水平方向(![]() 方向)と鉛直方向(
方向)と鉛直方向(![]() 方向)に分解して取り扱います.ここで,
方向)に分解して取り扱います.ここで,![]() 方向は等速運動を行い,
方向は等速運動を行い,![]() 方向は下向きに重力加速度
方向は下向きに重力加速度
![]() で等加速度運動するという特徴がありました.(水平投射の場合と同じ運動の特徴になります.)
で等加速度運動するという特徴がありました.(水平投射の場合と同じ運動の特徴になります.)
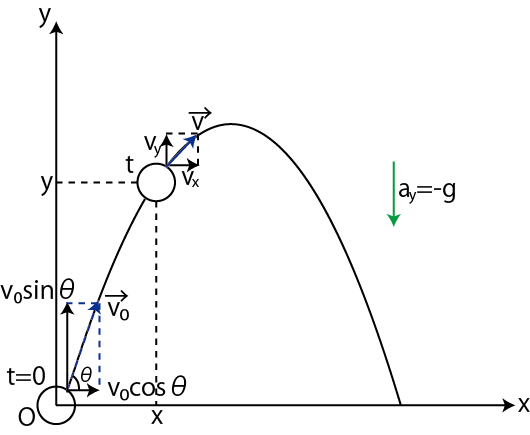
Figure8.5: 放物運動2
![]() 方向は等速運動するので,次式が成立します.
方向は等速運動するので,次式が成立します.
![]() 方向は初速度
方向は初速度
![]() ,加速度
,加速度
![]() の等加速度運動をするので,鉛直投げ上げと同じになります.(鉛直投げ上げの場合と同様に,
の等加速度運動をするので,鉛直投げ上げと同じになります.(鉛直投げ上げの場合と同様に,![]() 軸は上向きにとりました.)したがって,次式が成立します.
軸は上向きにとりました.)したがって,次式が成立します.
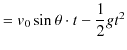 |
時間 ![]() を消去して,
を消去して,![]() と
と ![]() の関係を求めると次のようになります.
の関係を求めると次のようになります.
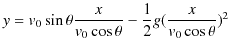 |
||
最後の関係式は図の中の物体が描く軌跡の方程式を意味しています.この式で,![]() とおくと,
とおくと,
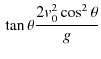 |
||
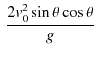 |
となります.したがって,水平到達距離 ![]() は次のようになります.
は次のようになります.
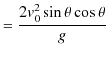 |
||
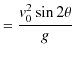 |
故に,![]() が最大値をとるときの
が最大値をとるときの
![]() は,
は,
というよく知られた結果になります.
落体の運動においては,保存力である重力のみがはたらいているので,力学的エネルギーが保存します.ただし,空気の抵抗力が無視できない場合は,熱が発生し力学的エネルギーは減少します.