Chapter7 例1（自由粒子と拘束運動）

7.1 自由粒子

宇宙空間のような無重力状態において，外からの場も存在せず，外力も加わっていない粒子を自由粒子と言います．この場合，慣性の法則により，自由粒子は静止しているか，あるいは等速直線運動をしています．このとき，速さが変わらず運動エネルギーは一定です．そして，場がないということは，ポテンシャルは $ 0[J]$ になります．従って，力学的エネルギー保存則が成立しています．また，速度が変わらず運動量も一定なので，運動量保存則も成立しています．

 

7.2 拘束運動

物体が直線や曲線，あるいは曲面の上でのみ運動を行うとき，その運動を拘束運動と言います．その際，直線や曲線，あるいは曲面から受ける力を拘束力と言います．拘束力の例としては，垂直抗力（水平面上の運動や斜面上の運動の場合等．），糸の張力（単振り子の場合等．），弾性力（ばね振り子の場合等．）等が挙げられます．

 

7.3 水平面上の運動

ここでは，拘束運動の例として，最も簡単な場合，すなわち，水平面上での運動を考えます．これから，考える幾つかの状況において，それぞれ(1)運動と力の関係（慣性の法則，または運動方程式），(2)運動エネルギーと仕事の関係（エネルギー原理），(3)運動量と力積の関係（運動量原理）で取り扱えることを確認していきます．まず，水平面が摩擦の無い理想的な状況で，置かれた物体に鉛直方向には重力と垂直抗力がつりあっていて，水平方向には力がはたらいていない場合を考えます．この場合，慣性の法則より，物体は静止しているか，あるいは等速直線運動をしています．このとき，運動エネルギーは一定で，高さが変わらないのでポテンシャルも変化せず，力学的エネルギー保存則は成立しています．また，運動量も一定なので，運動量保存則も成立しています．

　次に，なめらかな水平面上にある物体について，鉛直方向には重力と垂直抗力がつりあっていて，水平方向には一定の大きさの外力がはたらいている場合を考えます．外力 $ F[N]$ により，加速度 $ a[m/s^{2}]$ が生じますが，運動方程式 $ ma=F$ が成立します．力学的エネルギーについては，

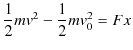
$\displaystyle \dfrac{1}{2}mv^{2}-\dfrac{1}{2}mv_{0}^{2}=Fx$

という式が成立しました．すなわち，

　"運動エネルギーの増加量は加えた仕事に等しくなります．"

というエネルギー原理が成り立ちます．運動量については，

$\displaystyle mv-mv_{0}=F\cdot\Delta t$

という式が成立しました．すなわち，

　"運動量の増加量は加えた力積に等しくなります．"

という運動量原理が成り立ちます．

　最後に，粗い水平面上にある物体について，鉛直方向には重力と垂直抗力がつりあっていて，水平方向には一定の大きさの動摩擦力が進行方向と逆向きにはたらいている場合を考えます．大きさ $ F'[N]$ の動摩擦力により負の加速度 $ a[m/s^{2}]$ が生じますが，運動方程式 $ ma=-F'$ が成立します．この場合，加速度は負，$ a<0$ になります．力学的エネルギーについては，

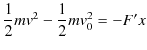
$\displaystyle \dfrac{1}{2}mv^{2}-\dfrac{1}{2}mv_{0}^{2}=-F'x$

という式が成立します．ここで，

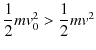
$\displaystyle \dfrac{1}{2}mv_{0}^{2}>\dfrac{1}{2}mv^{2}$

の大小関係があります．このとき，

　"運動エネルギーの減少量は負の仕事に等しくなります．"

というエネルギー原理が成り立ちます．運動量については，

$\displaystyle mv-mv_{0}=-F'\cdot\Delta t$

という式が成立します．ここで，

$\displaystyle mv_{0}>mv$

の大小関係があります．このとき，

　"運動量の減少量は負の力積に等しくなります．"

という運動量原理が成り立ちます．