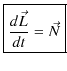Chapter6 角運動量
6.1 角運動量原理(運動方程式の第3の変形)
運動方程式の第3の変形を試みます.![]() 軸を中心に
軸を中心に ![]() 平面上を半径
平面上を半径 ![]() で接線方向に運動量の大きさ
で接線方向に運動量の大きさ
![]() の円運動している物体を考えます.
の円運動している物体を考えます.
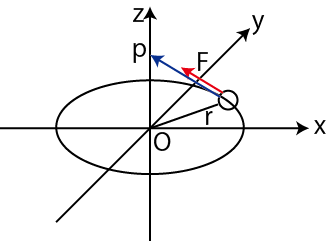
Figure6.1: 角運動量原理1
大きさ ![]() の力が円の接線方向に加わっている場合,円の接線方向について,次の運動方程式が成立します.
の力が円の接線方向に加わっている場合,円の接線方向について,次の運動方程式が成立します.
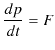
この方程式は大きさの関係を表しています.両辺を ![]() 倍すると次のようになります.
倍すると次のようになります.
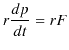 |
||
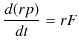 |
ここで,![]() 軸回りの角運動量
軸回りの角運動量
![]() と
と ![]() 軸回りのモーメント
軸回りのモーメント
![]() を次のように定義します.
を次のように定義します.
(ここでも理論の展開の中で物理量が定義されることに注意しましょう.)ここで,角運動量は物体の回転運動を表す物理量であり,モーメントは力の回転の能率を表す物理量です.このとき,上の式は,
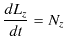
と表されることになります.すなわち,
"角運動量の時間微分はモーメントに等しくなります."
という関係が成立します.これを角運動量原理といいます.
次に,![]() 平面上の一般の運動を考えましょう.運動方程式は,
平面上の一般の運動を考えましょう.運動方程式は,
です.ただし,添え字の ![]() と
と ![]() はそれぞれの方向の成分を示します.ここで,
はそれぞれの方向の成分を示します.ここで,![]() ×(6.2)式-
×(6.2)式- ![]() ×(6.1)式をつくると次のようになります.
×(6.1)式をつくると次のようになります.
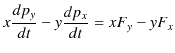
ここで,
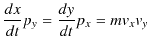
が成立するので,
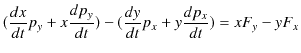 |
||
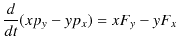 |
||
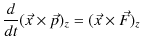 |
となります.ただし,最後の式の中の記号 ![]() はベクトル積を表します.
はベクトル積を表します.
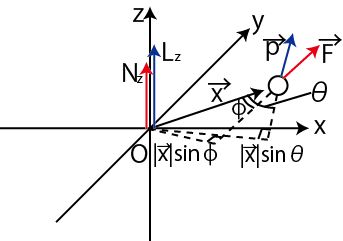
Figure6.2: 角運動量原理2
ここで,![]() 軸回りの角運動量
軸回りの角運動量
![]() と
と ![]() 軸回りのモーメント
軸回りのモーメント
![]() を次のように定義します.
を次のように定義します.
(ここでも理論の展開の中で,物理量が定義されていることに注意して下さい.)
![]() と
と
![]() は,それぞれベクトル積で表されているので,その大きさは次式で示されます.(図を参照して下さい.)
は,それぞれベクトル積で表されているので,その大きさは次式で示されます.(図を参照して下さい.)
このとき,
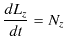
が成り立つことになります.すなわち,![]() 平面上の運動についても,
平面上の運動についても,
"角運動量の時間微分はモーメントに等しくなります."
という関係が成立します.
更に,一般の3次元空間上の運動について,運動方程式を変形し,同じ関係が成立することを見ておきましょう.運動方程式は次式です.
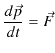
![]() と
と
![]() は同一方向ですが,その向きは任意である場合を考えています.この運動方程式の両辺に,左から位置ベクトル
は同一方向ですが,その向きは任意である場合を考えています.この運動方程式の両辺に,左から位置ベクトル
![]() をかけてベクトル積をとります.
をかけてベクトル積をとります.
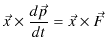
ここで,
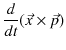 |
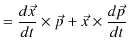 |
|
であることに注意します.
![]() と
と
![]() は向きが同じなので,そのベクトル積は 0 になります.また,右辺第2項は運動方程式を使いました.)故に,
は向きが同じなので,そのベクトル積は 0 になります.また,右辺第2項は運動方程式を使いました.)故に,
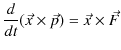
となります.この式の中で,角運動量
![]() とモーメント
とモーメント
![]() を次のように定義します.
を次のように定義します.
(ここでも理論の展開の中で物理量が定義されていることに注意して下さい.)このとき,上の式は,
となります.すなわち,3次元空間の中の一般の場合も,
原理6.1(角運動量原理) "角運動量の時間微分はモーメントに等しくなります."
という角運動量原理が成立します.
6.2 角運動量保存則
角運動量原理(6.3)式,
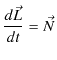
において,モーメントを
![]() とすると,
とすると,
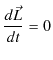
となります.すなわち,
法則6.1(角運動量保存則) "外力のモーメントが
![]() のとき,角運動量は一定になります."
のとき,角運動量は一定になります."
という角運動量保存則が成立することが理解されます.
以上の議論より,"ニュートンの法則" のChapterの "力学の体系" のSectionで述べたこと,つまり角運動量保存則はニュートンの三法則の枠内で導出されることが理解されます.(第二法則(運動の法則,つまり運動方程式)から導出されました.)