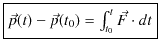Chapter5 運動量

5.1 運動量原理（運動方程式の第2の変形）

運動方程式の第2の変形を試みましょう．まず，直線運動している物体において，運動の向きに一定の力がはたらく場合を考えます．例えば，力学台車を一定の力で真っ直ぐに引くような場合を想定します．（運動の法則，エネルギー原理でも同様な状況を考えましたね．この1つの状況を3種類の方法で取り扱うことができるのです．3種類の方法というのは，(1)加速度と力，(2)運動エネルギーと仕事（エネルギー原理），そして今から見ていく，(3)運動量と力積（運動量原理）のそれぞれの関係です．）

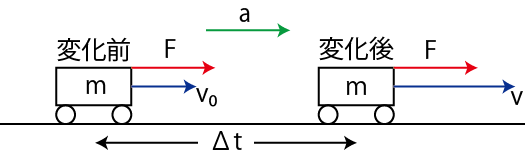
運動量原理

Figure5.1: 運動量原理

このとき，次式で表される一定の加速度 $ a[m/s^{2}]$ が生じます．

$\displaystyle a=\dfrac{v-v_{0}}{\Delta t}$

ここで，$ v[m/s]$ は終速度， $ v_{0}[m/s]$ は初速度， $ \Delta t[s]$ は力がはたらいている時間を表します．この式を運動方程式 $ ma=F$ に代入して変形すると，次のようになります．

  $\displaystyle m\dfrac{v-v_{0}}{\Delta t}=F$    
% latex2html id marker 332 $\displaystyle \therefore$ $\displaystyle mv-mv_{0}=F\cdot\Delta t$    

ここで，2つの物理量を定義します．左辺の質量と速度の積を運動量 $ p[kg\cdot m/s]$ と定義します．すなわち，

$\displaystyle p\equiv mv$

です．また，右辺の力と時間の積を力積 $ I[N\cdot s]$ と定義します．

$\displaystyle I\equiv F\cdot\Delta t$

このとき，

　"運動量の変化量は力積に等しくなります．"

という関係が成立します．（運動量と力積は理論の展開の中で定義されている物理量であることに注意しておきます．）すなわち，力をはたらかせ力積を加えると，運動が激しくなり，加えた力積の分だけ運動量が増大することになります．（力が運動の向きと逆向きの場合は運動量は減少します．）

　次に，時間的に変化する力が物体にはたらく場合を考えましょう．運動方程式は次のように変形されます．

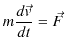  $\displaystyle m\dfrac{d\vec{v}}{dt}=\vec{F}$    
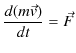% latex2html id marker 343 $\displaystyle \therefore$ $\displaystyle \dfrac{d(m\vec{v})}{dt}=\vec{F}$    

ここで，運動量 $ \vec{p}[kg\cdot m/s]$ を次式で定義します．

$\displaystyle \vec{p}\equiv m\vec{v}$

これは，先程の定義を向きまで含めて拡張したものになっています．このとき，運動方程式は，

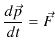
$\displaystyle \dfrac{d\vec{p}}{dt}=\vec{F}$

となります．故に，

$\displaystyle d\vec{p}=\vec{F}\cdot dt$

ですが，さらに，この式の両辺を力がはたらいている時間 $ t_{0}[s]$ から $ t[s]$ まで積分します．

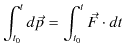
$\displaystyle \int_{t_{0}}^{t}d\vec{p}=\int_{t_{0}}^{t}\vec{F}\cdot dt$

故に，次式の関係が成立します．

$\displaystyle \fbox{$\vec{p}(t)-\vec{p}(t_{0})=\int_{t_{0}}^{t}\vec{F}\cdot dt$}$ (5.1)

この式の右辺の量を力積 $ \vec{I}[N\cdot s]$ として定義します．

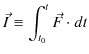
$\displaystyle \vec{I}\equiv\int_{t_{0}}^{t}\vec{F}\cdot dt$

（ここでも運動量と力積は理論の展開の中で定義されている物理量であることに注意しましょう．）したがって，力が変化する場合も，

原理5.1(運動量原理) "運動量の変化量は力積に等しくなります．"

という関係が成立します．この関係は運動方程式と等価です．

 

5.2 1物体系の運動量保存則

運動量原理(5.1)式，

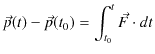
$\displaystyle \vec{p}(t)-\vec{p}(t_{0})=\int_{t_{0}}^{t}\vec{F}\cdot dt$

において，力が働かない場合，右辺は 0 になります．よって，

$\displaystyle \vec{p}(t)=\vec{p}(t_{0})$

となります．すなわち，運動量は時間的に変化しません．このことを1物体系の運動量保存則といいます．物体は等速直線運動しますが，この状況は慣性の法則そのものです．