Chapter4 力学的エネルギー

4.1 エネルギー原理（運動方程式第1の変形）

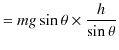これから3つのChapterにわたって，運動方程式を変形し，力学の法則を導くことを考えてみましょう．このChapterでは運動方程式の第1の変形を試みます．まず，直線運動している物体において，運動の向きに一定の力がはたらく場合を考えます．例えば，力学台車を一定の力で，真っ直ぐに引くような場合です．

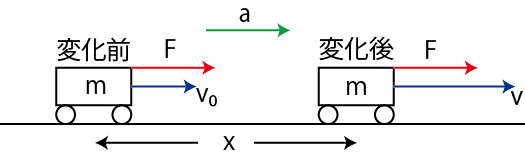
エネルギー原理

Figure4.1: エネルギー原理

このとき，物体は一定の加速度 $ a[m/s^{2}]$ の等加速度直線運動をするので，関係式，

$\displaystyle v^{2}-v_{0}^{2}=2ax$

が成立します．ここで，$ v[m/s]$ は終速度， $ v_{0}[m/s]$ は初速度，$ x[m]$ は移動距離です．この式は，運動方程式 $ ma=F$ より，次のように変形されます．

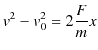  $\displaystyle v^{2}-v_{0}^{2}=2\dfrac{F}{m}x$    
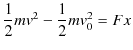% latex2html id marker 860 $\displaystyle \therefore$ $\displaystyle \dfrac{1}{2}mv^{2}-\dfrac{1}{2}mv_{0}^{2}=Fx$    

ここで，2つの物理量を定義します．すなわち，運動エネルギー $ T[J]$ と仕事 $ W[J]$ を次式で定めます．

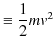$\displaystyle T$ $\displaystyle \equiv\dfrac{1}{2}mv^{2}$    
$\displaystyle W$ $\displaystyle \equiv Fx$    

このとき，

　"運動エネルギーの変化量は仕事に等しくなります．"

という関係が成立します．（理論の展開の中で物理量が定義されていることに注意して下さい．）図の場合では，力の向きと運動の向きが同じですが，このとき力は正の仕事をすると言います．正の仕事の分だけ，運動が激しくなり運動エネルギーが増大することになります．（力の向きと運動の向きが逆の場合，負の仕事をすると言いますが，このときは運動が穏やかになり，負の仕事の分だけ運動エネルギーが減少することになります．）

　一般に，力の大きさと向きが変化する場合を考えてみましょう．運動方程式，

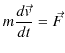
$\displaystyle m\dfrac{d\vec{v}}{dt}=\vec{F}$

の両辺に $ \vec{v}dt=d\vec{x}$ を掛けてスカラー積をとり，次のように変形します．ただし， $ d\vec{x}[m]$ は微小時間における変位ベクトルです．

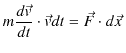  $\displaystyle m\dfrac{d\vec{v}}{dt}\cdot\vec{v}dt=\vec{F}\cdot d\vec{x}\,$    
% latex2html id marker 877 $\displaystyle \therefore$ $\displaystyle md\vec{v}\cdot\vec{v}=\vec{F}\cdot d\vec{x}$    
% latex2html id marker 879 $\displaystyle \therefore$ $\displaystyle mvdv=\vec{F}\cdot d\vec{x}$    
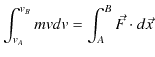% latex2html id marker 881 $\displaystyle \therefore$ $\displaystyle \int_{v_{A}}^{v_{B}}mvdv=\int_{A}^{B}\vec{F}\cdot d\vec{x}$    

よって，次式が成立します．

$\displaystyle \fbox{$\dfrac{1}{2}mv_{B}^{2}-\dfrac{1}{2}mv_{A}^{2}=\int_{A}^{B}\vec{F}\cdot d\vec{x}$}$ (4.1)

ただし，はじめの速度を $ v_{A}[m/s]$，はじめの位置を $ A$ ，終りの速度を $ v_{B}[m/s]$，終りの位置を $ B$ としました．ここで，運動エネルギー $ T[J]$ と仕事 $ W[J]$ を次式で定義します．

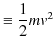$\displaystyle T$ $\displaystyle \equiv\dfrac{1}{2}mv^{2}$    
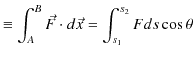$\displaystyle W$ $\displaystyle \equiv\int_{A}^{B}\vec{F}\cdot d\vec{x}=\int_{s_{1}}^{s_{2}}Fds\cos\theta$    

$ \theta[rad]$ はその瞬間における力 $ \vec{F}[N]$ と，その変位ベクトル $ d\vec{x}[m]$ のなす角であり，$ ds[m]$ は微小時間における変位ベクトル $ d\vec{x}[m]$ の大きさです．位置 $ A$ から位置 $ B$ までの積分は線積分です．（ここでも理論の展開の中で物理量が定義されていることに注意して下さい．）(4.1)式より，力が変化する場合も，

原理4.1(エネルギー原理) "運動エネルギーの変化量は仕事に等しくなります．"

という関係が成立することが理解されます．(4.1)式をエネルギー原理と言います．

 

4.2 仕事率

仕事の能率を表す物理量として，単位時間の仕事である仕事率 $ P[W]$（ワット）を次式で定義します．

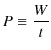
$\displaystyle P\equiv\dfrac{W}{t}$

$ [W]=[J/s]$ です．特に，力がつりあっていて，一定の速さ $ v[m/s]$ で運動しているときには次式が成立します．

$\displaystyle P$ $\displaystyle \equiv\dfrac{W}{t}$    
  $\displaystyle =\dfrac{Fx}{t}$    
% latex2html id marker 932 $\displaystyle \therefore P$ $\displaystyle =Fv$    

 

4.3 保存力とポテンシャル

仕事が最初の位置と最後の位置で決定され，途中の経路に依らないとき，はたらいている力を保存力と言います．保存力を $ \vec{F'}[N]$，保存力のする仕事を $ W'[J]$ と表すことにします．保存力の例としては，重力，弾性力，万有引力，クーロン力等が挙げられます．保存力の正の仕事 $ W'[J]$ により，物体が位置 $ A$ から基準の位置 $ O$ まで動いたとき，エネルギー原理(4.1)式から，物体の運動エネルギーは $ W'[J]$ だけ増加します．ということは，物体ははじめの位置 $ A$ にあるとき，すでに仕事をする能力，すなわちエネルギーをもっていたことになります．このエネルギーをポテンシャル $ V(A)[J]$ と定義します．基準の位置 $ O$ におけるポテンシャルを $ 0[J]$ ととると，

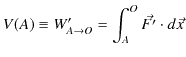
$\displaystyle V(A)\equiv W'_{A\to O}=\int_{A}^{O}\vec{F'}\cdot d\vec{x}$

となります．

　具体的なポテンシャルを求めておきましょう．まず，一様な重力によるポテンシャルを表します．最初に，鉛直下向きに物体が移動する場合を考えます．鉛直上向きに $ z$ 軸をとり，高さ $ 0[m]$ の基準におけるポテンシャルを $ 0[J]$ とします．

このとき，ポテンシャル $ V[J]$ は次のように計算されます．

$\displaystyle V=mg\times h=mgh$

次に，図 "ポテンシャル2" のように経路を2つ考え，それぞれのポテンシャルを計算してみます．経路1の場合，ポテンシャル $ V_{1}[J]$ は次のようになります．

$\displaystyle V_{1}$ $\displaystyle =mg\times h+mg\times0$    
  $\displaystyle =mgh$    

経路2の場合，ポテンシャル $ V_{2}[J]$ は次のようになります．

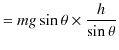$\displaystyle V_{2}$ $\displaystyle =mg\sin\theta\times\dfrac{h}{\sin\theta}$    
  $\displaystyle =mgh$    

経路1と経路2でポテンシャルは同じです．

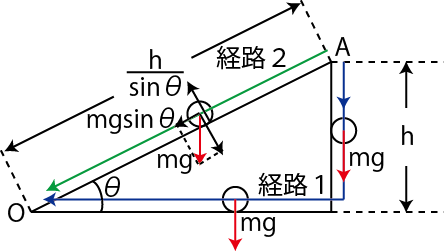
ポテンシャル2

Figure4.3: ポテンシャル2

一般に，重力がはたらいているとき，任意の経路について，ポテンシャルは次のように計算されます．

$\displaystyle V$ $\displaystyle \equiv W'_{A\to O}$    
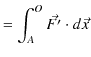  $\displaystyle =\int_{A}^{O}\vec{F'}\cdot d\vec{x}$    
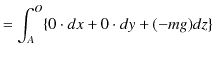  $\displaystyle =\int_{A}^{O}\{0\cdot dx+0\cdot dy+(-mg)dz\}$    
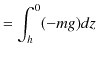  $\displaystyle =\int_{h}^{0}(-mg)dz$    
  $\displaystyle =mgh$    

確かに，重力によるポテンシャルは高さ $ h[m]$ だけで決まる量であることが理解されますね．

　次に，弾性力によるポテンシャルを求めておきます．ただし，ばねに沿って $ x$ 軸をとり，自然長の位置を $ x=0[m]$ とします．次のように計算されます．

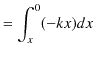$\displaystyle V$ $\displaystyle =\int_{x}^{0}(-kx)dx$    
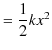  $\displaystyle =[-\dfrac{1}{2}kx^{2}]_{x}^{0}$    
  $\displaystyle =\dfrac{1}{2}kx^{2}$    

　それでは，保存力をポテンシャルで表す式を導いておきましょう．

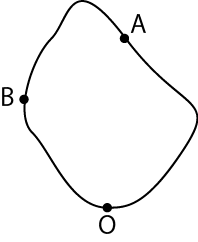
ポテンシャル3

Figure4.4: ポテンシャル3

$\displaystyle W'_{A\to B}$ $\displaystyle =W'_{A\to O\to B}$    
  $\displaystyle =W'_{A\to O}+W'_{O\to B}$    
  $\displaystyle =W'_{A\to O}-W'_{B\to O}$    
% latex2html id marker 1009 $\displaystyle \therefore W'_{A\to B}$ $\displaystyle =V(A)-V(B)$    

計算を続けます．

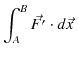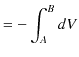$\displaystyle \int_{A}^{B}\vec{F'}\cdot d\vec{x}\,$ $\displaystyle =-\int_{A}^{B}dV$    
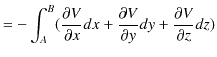  $\displaystyle =-\int_{A}^{B}(\dfrac{\partial V}{\partial x}dx+\dfrac{\partial V}{\partial y}dy+\dfrac{\partial V}{\partial z}dz)$    
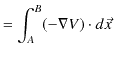  $\displaystyle =\int_{A}^{B}(-\nabla V)\cdot d\vec{x}$    

ですから，次の関係式が成立します．

$\displaystyle \fbox{$\vec{F'}=-\nabla V(\vec{x})$}$ (4.2)

ただし，記号ナブラ，

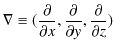
$\displaystyle \nabla\equiv(\dfrac{\partial}{\partial x},\dfrac{\partial}{\partial y},\dfrac{\partial}{\partial z})$

を使っています．保存力は(4.2)式により，ポテンシャル $ V[J]$ で表されます．逆に，力がポテンシャルにより(4.2)式で導かれる場合，その力は保存力になります．

　話は前後しますが，3番目のポテンシャルの例として，万有引力によるポテンシャルを求めることにします．次のように計算されます．

$\displaystyle V(A)-V(\infty)$ $\displaystyle =W'_{A\to\infty}$    
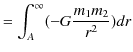  $\displaystyle =\int_{A}^{\infty}(-G\dfrac{m_{1}m_{2}}{r^{2}})dr$    
  $\displaystyle =Gm_{1}m_{2}[\dfrac{1}{r}]_{A}^{\infty}$    
  $\displaystyle =-G\dfrac{m_{1}m_{2}}{r_{A}}$    

$ A$ 点での $ r[m]$ である $ r_{A}[m]$ を，改めて $ r[m]$ とおき直すと，

$\displaystyle V=-G\dfrac{m_{1}m_{2}}{r}$

となります．

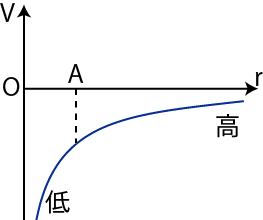
ポテンシャル4

Figure4.5: ポテンシャル4

万有引力は引力なのでポテンシャルは負の値をとります．これは，遠く離れる程近づく可能性が生じるので高いエネルギーになり，その最も大きなエネルギーをもつ無限遠のポテンシャルの値を基準として $ 0[J]$ にしたことによります．

 

4.4 力学的エネルギー保存則

保存力のみが仕事をする場合，エネルギーの間にどのような関係が成立するでしょうか？ 簡単な場合から見ておきます．まず，図のようになめらかな摩擦の無い曲がった斜面を下る物体について考えてみます．

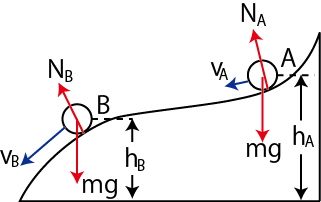
力学的エネルギー保存則1

Figure4.6: 力学的エネルギー保存則1

物体は $ A$ から $ B$ へ移動しますが，その間，常に垂直抗力は進行方向と直交していますので，する仕事は $ 0[J]$ です．保存力である重力のみが仕事をすることになります．ここで，"運動エネルギーの変化量は仕事に等しい．" というエネルギー原理より，次のように計算されます．

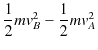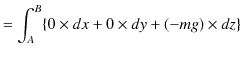$\displaystyle \dfrac{1}{2}mv_{B}^{2}-\dfrac{1}{2}mv_{A}^{2}$ $\displaystyle =\int_{A}^{B}\{0\times dx+0\times dy+(-mg)\times dz\}$    
  $\displaystyle =[-mgz]_{A}^{B}$    
  $\displaystyle =-mgh_{B}+mgh_{A}$    

よって，結論は，

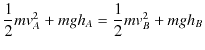
$\displaystyle \dfrac{1}{2}mv_{A}^{2}+mgh_{A}=\dfrac{1}{2}mv_{B}^{2}+mgh_{B}$

です．最後の式は運動エネルギーとポテンシャルの和が一定であることを示しています．ここで，運動エネルギーとポテンシャルのことを力学的エネルギーと呼ぶことにしましょう．保存力である重力のみが仕事をするとき，力学的エネルギーの和は保存するのです．

　次に，水平ばね振り子について見ておきます．

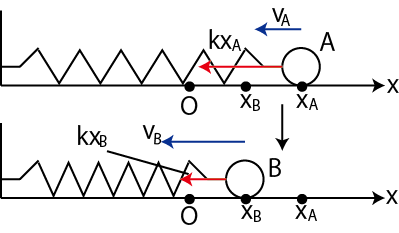
力学的エネルギー保存則2

Figure4.7: 力学的エネルギー保存則2

この場合，保存力である弾性力のみが仕事をしています．ここで，"運動エネルギーの変化量は仕事に等しい．" というエネルギー原理より，次のように計算されます．

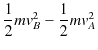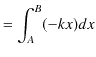$\displaystyle \dfrac{1}{2}mv_{B}^{2}-\dfrac{1}{2}mv_{A}^{2}$ $\displaystyle =\int_{A}^{B}(-kx)dx$    
  $\displaystyle =[-\dfrac{1}{2}kx^{2}]_{A}^{B}$    
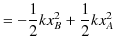  $\displaystyle =-\dfrac{1}{2}kx_{B}^{2}+\dfrac{1}{2}kx_{A}^{2}$    

よって，結論は，

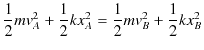
$\displaystyle \dfrac{1}{2}mv_{A}^{2}+\dfrac{1}{2}kx_{A}^{2}=\dfrac{1}{2}mv_{B}^{2}+\dfrac{1}{2}kx_{B}^{2}$

です．最後の式は運動エネルギーとポテンシャルの和，すなわち力学的エネルギーの和が一定であることを示しています．

　一般に，保存力のみが仕事をする場合，

$\displaystyle W'_{A\to B}=V(A)-V(B)$

が成立しますが，左辺の保存力による仕事 $ W'[J]$ により，(4.1)式のように運動エネルギーが変化します．故に，

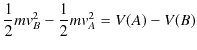  $\displaystyle \dfrac{1}{2}mv_{B}^{2}-\dfrac{1}{2}mv_{A}^{2}=V(A)-V(B)$    
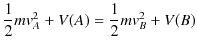% latex2html id marker 1074 $\displaystyle \therefore$ $\displaystyle \dfrac{1}{2}mv_{A}^{2}+V(A)=\dfrac{1}{2}mv_{B}^{2}+V(B)$    
% latex2html id marker 1076 $\displaystyle \therefore$ $\displaystyle T+V=E(const)$    

という関係が導かれました．すなわち，

法則4.1(力学的エネルギー保存則) "保存力のみが仕事をする場合，力学的エネルギーの和は一定です．"

という力学的エネルギー保存則が成立することが理解されます．以上の議論によりニュートンの法則のChapterの中の力学の体系のSectionで述べたこと，力学的エネルギー保存則はニュートンの3法則の枠内で導出されることが理解されました．（第二法則（運動の法則，つまり運動方程式）から導出されました．）ところで，保存力以外の力（これを非保存力といいます．）が仕事をする場合，力学的エネルギー保存則は成立しません．非保存力の例としては，動摩擦力，空気の抵抗力等が挙げられますが，そのような力がはたらく場合には熱が発生し，力学的エネルギーは減少します．