Chapter8 アンペール力とローレンツ力

8.1 アンペール力

静磁場中で定常電流が流れると力を受けます．この力をアンペール力といいます．定常電流と静磁場が垂直の場合，アンペール力の向きに関して，フレミングの左手の法則が成立します．すなわち，左手の3つの指をそれぞれ垂直になるようにして，中指が定常電流の向き，人差し指が静磁場の向き，親指がアンペール力の向きです．

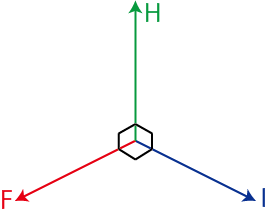
アンペール力1

Figure8.1: アンペール力1

このときのアンペール力の大きさ $ F[N]$ は，定常電流の強さ $ I[A]$，静磁場の強さ $ H[A/m]$，導線の長さ $ \ell[m]$ に比例します．すなわち，

$\displaystyle F=\mu_{0}IH\ell=IB\ell$

と表されます．ただし，

$\displaystyle \mu_{0}=4\pi\times10^{-7}[N/A^{2}]$

は比例定数の真空の透磁率であり，磁束密度 $ B[T]$ には，

$\displaystyle B=\mu_{0}H$

の関係があります．定常電流と静磁場が $ \theta$ の角をなすときは，静磁場 $ H[A/m]$ に垂直な導線の長さ $ \ell\sin\theta[m]$ がアンペール力の大きさ $ F[N]$ に関係します．したがって，アンペール力の大きさ $ F[N]$ は，

$\displaystyle F=\mu_{0}IH\ell\sin\theta=IB\ell\sin\theta$

となります．一般にアンペール力の大きさと向きを含めて，ベクトルを使って表すと，

$\displaystyle \vec{F}=\mu_{0}I\vec{\ell}\times\vec{H}=I\vec{\ell}\times\vec{B}\,$

となります．ただし，ベクトル積を使いました．ここで，導線の長さを微小にとり， $ I\Delta\vec{s}[A\cdot m]$ で表される電流素片というものを考えましょう．このとき，電流素片から生じた微小なアンペール力 $ \Delta\vec{F}[N]$ は次式で表されます．

$\displaystyle \Delta\vec{F}=I\Delta\vec{s}\times\vec{B}$

微小量を限りなく 0 に近づけると，次式が成立します．

$\displaystyle d\vec{F}=Id\vec{s}\times\vec{B}$ (8.1)

　アンペール力の一つの例として，2本の平行電流間に働く力を考えましょう．

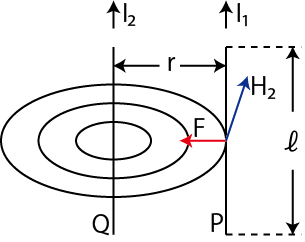
アンペール力2

Figure8.2: アンペール力2

導線 $ Q$ に流れる定常電流が導線 $ P$ の位置でつくる静磁場の大きさ $ H_{2}[A/m]$ は，

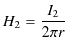
$\displaystyle H_{2}=\dfrac{I_{2}}{2\pi r}$

です．静磁場の向きは右ねじの法則により，図のように生じることがわかります．したがって，導線 $ P$ の長さ $ \ell[m]$ の部分が受ける力の大きさ $ F[N]$ は，

$\displaystyle F$ $\displaystyle =\mu_{0}I_{1}H_{2}\ell$    
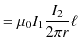  $\displaystyle =\mu_{0}I_{1}\dfrac{I_{2}}{2\pi r}\ell$    
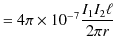  $\displaystyle =4\pi\times10^{-7}\dfrac{I_{1}I_{2}\ell}{2\pi r}$    
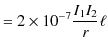  $\displaystyle =2\times10^{-7}\dfrac{I_{1}I_{2}}{r}\ell$    

となります．力の向きはフレミングの左手の法則より引力となります．導線 $ P$ に流れる定常電流が導線 $ Q$ に及ぼす引力の大きさも同じ最後の式になります．（定常電流の向きがお互いに逆向きのときは斥力が働きます．）最後の式を利用して定常電流の単位 $ [A]$ を定義します．

定義8.1(定常電流の単位) "$ 1[A]$ とは，真空中で $ 1[m]$ 隔てて平行に置かれた2本の導線に同じ強さの定常電流を流したとき，導線どうしが及ぼし合う力の大きさが $ 1[m]$ あたり， $ 2\times10^{-7}[N]$ のときの定常電流の強さとします．"

 

8.2 ローレンツ力

定常電流が静磁場の中で力を受けるということは，定常電流は荷電粒子の流れですので，その荷電粒子１つ１つに力がかかっていることになります．静磁場中で運動する１個の荷電粒子が受ける力をローレンツ力といいます．磁束密度 $ B[T]$ の中で電荷 $ q[C]$ の荷電粒子が受けるローレンツ力を，アンペール力の表式(8.1)式，

$\displaystyle d\vec{F}=Id\vec{s}\times\vec{B}$

から導出しましょう．定常電流の大きさは，

$\displaystyle I=qnvS$

でした．ここで， $ n[1/m^{3}]$ は単位体積中の荷電粒子の数，$ v[m/s]$ は荷電粒子の速度，$ S[m^{2}]$ は導線の断面積です．故に，

$\displaystyle d\vec{F}$ $\displaystyle =Id\vec{s}\times\vec{B}$    
  $\displaystyle =qnvS\cdot d\vec{s}\times\vec{B}$    
  $\displaystyle =nSds\cdot q\vec{v}\times\vec{B}$    

となります．ここで，$ nSds$[個]は荷電粒子の数なので，ローレンツ力は，

$\displaystyle \vec{F}=q\vec{v}\times\vec{B}$

と求められます．また，静磁場と静電場が生じているときに運動する荷電粒子が受ける力は次式で表されます．

$\displaystyle \fbox{$\vec{F}=q\vec{E}+q\vec{v}\times\vec{B}$}$ (8.2)

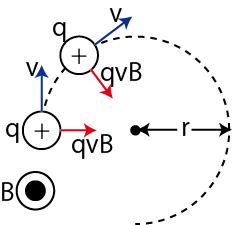
　実際に，荷電粒子静磁場中に初速度 $ v[m/s]$ で打ち込むと，進行方向に対して常に垂直にローレンツ力がかかり，粒子は等速円運動をします．向心力の役目をしているのは，ローレンツ力です．

ローレンツ力

Figure8.3: ローレンツ力

ここで，磁束密度 $ B[T]$ は図の紙面の裏から表向きにかかっている場合を考えています．円の中心方向への運動方程式の大きさの関係より，次のように円の半径が求められます．

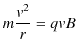  $\displaystyle m\dfrac{v^{2}}{r}=qvB$    
% latex2html id marker 551 $\displaystyle \therefore$ $\displaystyle mv^{2}=qvBr$    
% latex2html id marker 553 $\displaystyle \therefore$ $\displaystyle r=\dfrac{mv}{qB}$    

また，周期 $ T[s]$ も計算されます．

$\displaystyle T$ $\displaystyle =\dfrac{2\pi r}{v}$    
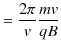  $\displaystyle =\dfrac{2\pi}{v}\dfrac{mv}{qB}$    
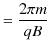  $\displaystyle =\dfrac{2\pi m}{qB}$    

周期は荷電粒子の速さに依存しないことがわかります．