Chapter7 静磁荷・静磁場・静磁位

7.1 静磁荷

静磁荷とは動いていない磁気の量のことであり，静電荷とよく似た物理量です．通常，N極を正，S極を負で表します．同極同士は反発し合い，異極同士は引き合います．静磁荷が静電荷と著しく違う点は，磁気単極子，すなわち，N極だけの静磁荷，S極だけの静磁荷は存在しないということです．N極とS極は常にペアになっています．また，静磁荷の単位には $ [Wb]$（ウェーバ）を使います．

　2つの静磁荷の間に働き合う静磁気力（クーロン力）の大きさ $ F[N]$ は，次式で表されます．

$\displaystyle F=k_{m}\dfrac{q_{m1}q_{m2}}{r^{2}}$ (7.1)

この関係もクーロンの法則といいます．ただし， $ k_{m}[N\cdot m^{2}/Wb^{2}]$ はクーロンの比例定数であり，

$\displaystyle k_{m}=\dfrac{10^{7}}{(4\pi)^{2}}[N\cdot m^{2}/Wb^{2}]$

です．また， $ q_{m1}[Wb],q_{m2}[Wb]$ は静磁荷，$ r[m]$ は静磁荷の間の距離です． $ q_{m1}[Wb],q_{m2}[Wb]$ が異符号のときは引力が，同符号のときは斥力が働き合います．

 

7.2 静磁場

静磁荷に関するクーロンの法則(7.1)式は，そのままでは遠隔作用による表式になっています．静電場の場合と同様に，この(7.1)式を変形して近接作用の概念を式の上で表すことにしましょう．変形は簡単です．

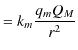$\displaystyle F$ $\displaystyle =k_{m}\dfrac{q_{m}Q_{M}}{r^{2}}$    
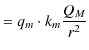  $\displaystyle =q_{m}\cdot k_{m}\dfrac{Q_{M}}{r^{2}}$    

ここで，

$\displaystyle H=k_{m}\dfrac{Q_{M}}{r^{2}}$ (7.2)

とおき，これを静磁場と呼びます．このとき，

$\displaystyle F=q_{m}H$ (7.3)

が成立します．この式が近接作用の概念を式で表したものです．すなわち，静磁荷 $ q_{m}[Wb]$ に作用するクーロン力 $ F[N]$ は，空間に生じている静磁場 $ H[N/Wb]$ から働きます．

　静磁荷に関するクーロンの法則(7.1)式は，静電荷に関するクーロンの法則と同形になっています．したがって，静磁場に関する式(7.2)式と(7.3)式も静電場に関する式と同形になっています．故に，静電場の場合と全く同様の議論による結論を，静磁場に対しても適用することができます．静電場に関するガウスの法則（積分形），

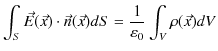
$\displaystyle \int_{S}\vec{E}(\vec{x})\cdot\vec{n}(\vec{x})dS=\dfrac{1}{\varepsilon_{0}}\int_{V}\rho(\vec{x})dV$

を参照して，磁場に関して，

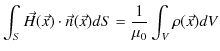
$\displaystyle \int_{S}\vec{H}(\vec{x})\cdot\vec{n}(\vec{x})dS=\dfrac{1}{\mu_{0}}\int_{V}\rho(\vec{x})dV$

が導けます．ここで，

$\displaystyle \varepsilon_{0}\equiv\dfrac{1}{4\pi k_{0}}[F/m]$

の式と同様に，

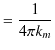$\displaystyle \mu_{0}$ $\displaystyle =\dfrac{1}{4\pi k_{m}}$    
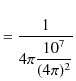  $\displaystyle =\dfrac{1}{4\pi\dfrac{10^{7}}{(4\pi)^{2}}}$    
  $\displaystyle =4\pi\times10^{-7}[N/A^{2}]$    

となります． $ \mu_{0}[N/A^{2}]$ を真空の透磁率と言います．上式をさらに変形して，

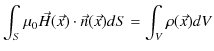
$\displaystyle \int_{S}\mu_{0}\vec{H}(\vec{x})\cdot\vec{n}(\vec{x})dS=\int_{V}\rho(\vec{x})dV$

とします．ここで，

$\displaystyle \vec{B}(\vec{x})\equiv\mu_{0}\vec{H}(\vec{x})$

として，静磁場に真空の透磁率を掛けた物理量を，磁束密度 $ \vec{B}(\vec{x})$ として定義します． $ \vec{B}(\vec{x})$ の単位は $ [T]$（テスラ）です．このとき，

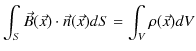
$\displaystyle \int_{S}\vec{B}(\vec{x})\cdot\vec{n}(\vec{x})dS=\int_{V}\rho(\vec{x})dV$

となります．ここで，静電荷にはなかった静磁荷特有の事情として，磁気単極子は存在しないということを考えましょう．N極とS極は常にペアで存在したので，静磁荷の総量はいつも $ 0[Wb]$ になります．したがって，右辺の体積分は 0 になります．よって，

$\displaystyle \fbox{$\int_{S}\vec{B}(\vec{x})\cdot\vec{n}(\vec{x})dS=0$}$ (7.4)

という静磁場に関するガウスの法則（積分形）が成立します．

　ベクトル解析のガウスの定理，つまり，任意のベクトル $ \vec{A}(\vec{x})\,$ について，

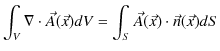
$\displaystyle \int_{V}\nabla\cdot\vec{A}(\vec{x})dV=\int_{S}\vec{A}(\vec{x})\cdot\vec{n}(\vec{x})dS$

が成立したことを思い出します．(7.4)式は，

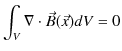
$\displaystyle \int_{V}\nabla\cdot\vec{B}(\vec{x})dV=0$

となります．ここで，被積分関数が 0 になりますので，

$\displaystyle \fbox{$\nabla\cdot\vec{B}(\vec{x})=0$}$ (7.5)

という，静磁場に関するガウスの法則（微分形）が成立します．

 

7.3 静磁位

静電荷・静電場・静電位の関係と同じように，静磁荷・静磁場・静磁位の関係が存在します．静磁位とは，静磁場に対する高低の概念をポテンシャルで表した物理量です．静電位のChapterで通常の高低の概念が重力によるポテンシャルの大小によって表されることを見ましたが，それを復習しておきます．

　普通，高いとか低いとかいう概念は重力が働いている場合に使います．物体は重力を受けて，自然に高いところから低いところへ移動します．もし，重力が働かない無重力状態にいれば，高低の概念は成立しないことになります．通常，高さは地面からの距離で測りますが，その代わりにポテンシャル $ mgh[J]$ をもちいても表すことができます．つまり，$ mgh[J]$ が大きい程高いということになります．特に，質量 $ m[kg]$ の重みを除いた $ gh[m^{2}/s^{2}]$ の部分が高さを表すと考えてよいでしょう．

　点電荷の周りの静電位について復習しておきます．簡単のため，2つの点電荷がともに正の場合を取り扱います．点電荷 $ Q[C]$ の周りに電場が生じているとします．ここで，点電荷 $ q[C]$ を置くとクーロン力が働き自然に移動しますが，高い方から低い方へ動くと考えます．すなわち，点電荷 $ Q[C]$ に近い方が高く，遠い方が低くなります．この高低をポテンシャルで表します．万有引力の場合と同じように，次の計算を行います．

$\displaystyle V(A)-V(\infty)$ $\displaystyle =W'_{A\to\infty}$    
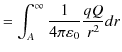  $\displaystyle =\int_{A}^{\infty}\dfrac{1}{4\pi\varepsilon_{0}}\dfrac{qQ}{r^{2}}dr$    
  $\displaystyle =\dfrac{qQ}{4\pi\varepsilon_{0}}[-\dfrac{1}{r}]_{A}^{\infty}$    
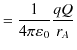  $\displaystyle =\dfrac{1}{4\pi\varepsilon_{0}}\dfrac{qQ}{r_{A}}$    

ここで，無限遠をポテンシャルの基準として， $ V(\infty)=0[J]$ とすると，距離 $ r[m]$ におけるポテンシャルは次式になります．

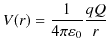
$\displaystyle V(r)=\dfrac{1}{4\pi\varepsilon_{0}}\dfrac{qQ}{r}$

この式を $ q[C]$ の重みと，残りの高さを表す量，すなわち静電位 $ \phi(r)[V]$ に分解します．（ $ V(r)=q\phi(r)$．）ここで，

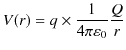
$\displaystyle V(r)=q\times\dfrac{1}{4\pi\varepsilon_{0}}\dfrac{Q}{r}$

より，静電位 $ \phi(r)[V]$ は次式になります．

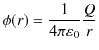
$\displaystyle \phi(r)=\dfrac{1}{4\pi\varepsilon_{0}}\dfrac{Q}{r}$

同様の議論により，静磁荷 $ Q_{M}[Wb]$ による静磁位は，

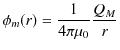
$\displaystyle \phi_{m}(r)=\dfrac{1}{4\pi\mu_{0}}\dfrac{Q_{M}}{r}$

となります．

　静電場と静電位の間の関係式，

$\displaystyle \vec{E}(\vec{x})=-\nabla\phi(\vec{x})$

と同様に，静磁場と静磁位の間には，

$\displaystyle \vec{H}(\vec{x})=-\nabla\phi_{m}(\vec{x})$

が成立します．ここで，$ A$ 点から $ B$ 点まで静磁場を線積分して計算していきます．

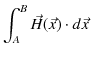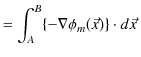$\displaystyle \int_{A}^{B}\vec{H}(\vec{x})\cdot d\vec{x}$ $\displaystyle =\int_{A}^{B}\{-\nabla\phi_{m}(\vec{x})\}\cdot d\vec{x}\,$    
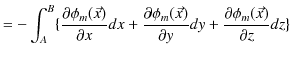  $\displaystyle =-\int_{A}^{B}\{\dfrac{\partial\phi_{m}(\vec{x})}{\partial x}dx+\... ...i_{m}(\vec{x})}{\partial y}dy+\dfrac{\partial\phi_{m}(\vec{x})}{\partial z}dz\}$    
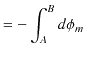  $\displaystyle =-\int_{A}^{B}d\phi_{m}$    
  $\displaystyle =\phi_{m}(A)-\phi_{m}(B)$    

したがって，

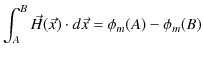
$\displaystyle \int_{A}^{B}\vec{H}(\vec{x})\cdot d\vec{x}=\phi_{m}(A)-\phi_{m}(B)$

が成立します．