Chapter6 定常電流と静電場

6.1 電流密度と電流保存則

電荷が移動した場合，その電荷の流れを電流といいます．電流 $ I[A]$ は単位時間に移動する電荷の量であり，移動した電荷の量を $ Q[C]$ として，次の関係式が成立します．

$\displaystyle I$ $\displaystyle =\dfrac{Q}{t}$    
$\displaystyle Q$ $\displaystyle =It$    

ここで，$ t[s]$ は時間です．

　電子の移動速度 $ v[m/s]$ と電流の強さ $ I[A]$ の関係を求めましょう．電子の電荷を $ -e[C]$，単位体積中の電子数を $ n[$個$ /m^{3}]$，導体の断面積を $ S[m^{2}]$ とすると， $ \Delta t[s]$ 間に断面積 $ S[m^{2}]$ を通過する電子数は $ n\cdot v\Delta tS[$個$ ]$ になります．故に，電流の強さ $ I[A]$ は，

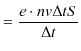$\displaystyle I$ $\displaystyle =\dfrac{e\cdot nv\Delta tS}{\Delta t}$    
  $\displaystyle =envS$    

となります．ここで，単位面積当たりの電流を考えて，電流密度 $ i[A/m^{2}]$ を定義します．すなわち，

$\displaystyle i$ $\displaystyle \equiv\dfrac{I}{S}$    
  $\displaystyle =env$    

となります．ここで，電流密度の向きも考えて，

$\displaystyle \vec{i}=en\vec{v}\,$

としておきます．

　一般に，電流密度は時間と位置の関数です．

$\displaystyle \vec{i}=\vec{i}(t,\vec{x})$

特に，時間に依らない場合，すなわち，

$\displaystyle \vec{i}=\vec{i}(\vec{x})$

のときの電流を定常電流といいます．今後，特に断らない限り，電流といえば定常電流のことを意味することにします．図のように導線を通過する電流は導線上のどの断面をとっても同じ値になります．

$\displaystyle I_{1}=I_{2}$

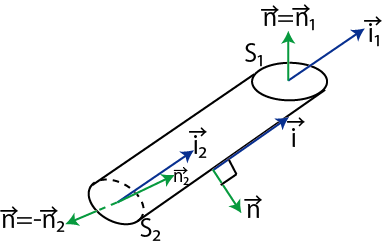
電流保存則

Figure6.1: 電流保存則

したがって，

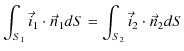  $\displaystyle \int_{S_{1}}\vec{i}_{1}\cdot\vec{n}_{1}dS=\int_{S_{2}}\vec{i}_{2}\cdot\vec{n}_{2}dS$    
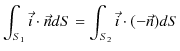% latex2html id marker 815 $\displaystyle \therefore$ $\displaystyle \int_{S_{1}}\vec{i}\cdot\vec{n}dS=\int_{S_{2}}\vec{i}\cdot(-\vec{n})dS$    
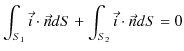% latex2html id marker 817 $\displaystyle \therefore$ $\displaystyle \int_{S_{1}}\vec{i}\cdot\vec{n}dS+\int_{S_{2}}\vec{i}\cdot\vec{n}dS=0$    

となります．ただし，$ \vec{n}\,$ は法線ベクトルです．また，側面では，

$\displaystyle \vec{i}\cdot\vec{n}=0$

となり面積分に寄与しません．したがって，閉曲面 $ S$（図の $ S_{1}$，$ S_{2}$ と側面の全体の曲面．）について面積分すると，

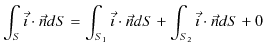  $\displaystyle \int_{S}\vec{i}\cdot\vec{n}dS=\int_{S_{1}}\vec{i}\cdot\vec{n}dS+\int_{S_{2}}\vec{i}\cdot\vec{n}dS+0$    
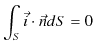% latex2html id marker 830 $\displaystyle \therefore$ $\displaystyle \int_{S}\vec{i}\cdot\vec{n}dS=0$    

となります．これが電流保存則の積分形になります．ここで，ベクトル解析のガウスの定理，（$ \vec{A}\,$ は任意のベクトルです．）

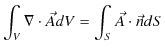
$\displaystyle \int_{V}\nabla\cdot\vec{A}dV=\int_{S}\vec{A}\cdot\vec{n}dS$

より，

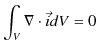  $\displaystyle \int_{V}\nabla\cdot\vec{i}dV=0$    
% latex2html id marker 837 $\displaystyle \therefore$ $\displaystyle \nabla\vec{i}=0$    

が成立します．最後の式が電流保存則の微分形になります．

 

6.2 オームの法則

抵抗上の2点間の電位差を $ \phi_{12}[V]$ とすると，その2点間に流れる電流の強さ $ I[A]$ は電位差 $ \phi_{12}[V]$ に比例します．比例定数を $ 1/R[1/\Omega]$ とおくと，

$\displaystyle I=\dfrac{\phi_{12}}{R}$

が成立します．この関係をオームの法則といいます．$ R$ の単位は $ [\Omega]$（オーム）です．このオームの法則を簡単な電気伝導のモデルから導出してみましょう．ここで，抵抗に電位差 $ \phi_{12}[V]$ がかかっていて，一定の電流 $ I[A]$ が流れている場合を考えます．抵抗の長さを $ \ell[m]$ とすると，抵抗内の一様な電場の強さは，

$\displaystyle \dfrac{\phi_{12}}{\ell}$

であり，よって電子に働くクーロン力は，電気素量を $ e[C]$ として，

$\displaystyle e\cdot\dfrac{\phi_{12}}{\ell}$

となります．この力が，速度の大きさに比例する抵抗力 $ kv[N]$（$ k[kg/s]$ は比例定数）につりあっています．（定常電流の場合，電子は等速運動していますので，慣性の法則が適用されます．）

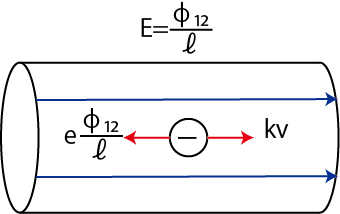
オームの法則

Figure6.2: オームの法則

故に，以下のようにオームの法則が導出されます．力のつりあいの式より，

  $\displaystyle e\cdot\dfrac{\phi_{12}}{\ell}=kv$    
% latex2html id marker 875 $\displaystyle \therefore$ $\displaystyle v=\dfrac{e\phi_{12}}{k\ell}$    

となります．ここで，関係式 $ I=envS$ より，

$\displaystyle I$ $\displaystyle =en\dfrac{e\phi_{12}}{k\ell}S$    
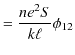  $\displaystyle =\dfrac{ne^{2}S}{k\ell}\phi_{12}$    
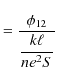  $\displaystyle =\dfrac{\phi_{12}}{\dfrac{k\ell}{ne^{2}S}}$    

となります．ここで，

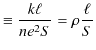$\displaystyle R$ $\displaystyle \equiv\dfrac{k\ell}{ne^{2}S}=\rho\dfrac{\ell}{S}$    
$\displaystyle \rho$ $\displaystyle \equiv\dfrac{k}{ne^{2}}$    

とおくと，オームの法則，

$\displaystyle I=\dfrac{\phi_{12}}{R}$

が成立することが確認できます．

 

6.3 電流回路

電流回路は抵抗と電池からなるものですが，その問題の解決において根本的な関係は，次に示す "電流回路を解く3つの鍵" です．

  1. 電流保存（キルヒホッフの第一法則）
  2. 電位の関係（キルヒホッフの第二法則）
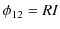
  3. オームの法則: $ \phi_{12}=RI$

鍵1の電流保存が成立する理由は電荷保存の法則によります．回路網中の任意の一点において，"（流れ込む電流の総和）＝（流れ出す電流の総和）" という関係が成立します．鍵2の電位の関係においては，抵抗による電位降下と，電池による起電力の分だけ電位上昇（化学エネルギーによります．），それに理想的な導線は等電位（理想的導線とは抵抗 $ 0[\Omega]$ の導線のことをいいます．オームの法則で $ R=0[\Omega]$ とすると，電位差 $ 0[V]$ になり等電位になります．）であることに注意しましょう．これらのことにより，任意の閉回路において，"（起電力の和）＝（抵抗による電位降下の和）" という関係が成立します．つまり，閉回路において，電位が電池で上がった分だけ抵抗で下がるのです．よって，一周回ると電位は元に戻ることになります．このことは，一つの点において電位は一つの値しか持たないので当然の結論です．直列回路，並列回路において成立する関係式は，この3つの鍵を用いて導くことができます．また，複雑な電流回路でも，ほとんどの場合この3つの鍵を考えれば解決することができます．

　最も簡単な電流回路から見ていきましょう．最も簡単な電流回路とは図のように，抵抗が1個と電池が1個だけから構成される回路のことをいいます．

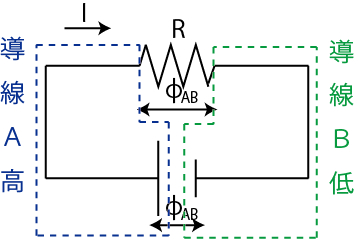
電流回路1

Figure6.3: 電流回路1

図のように，左側の導線 $ A$ と右側の導線 $ B$ に分けて考えます．鍵1の電流の保存は当然成立しています．（閉回路は1つしかありません．電流は各点で同じになります．）鍵2の電位の関係について見ておきます．抵抗値 $ 0[\Omega]$ の理想的な導線は等電位であるということから，導線 $ A$ と導線 $ B$ はそれぞれ等電位になります．導線 $ A$ の方が高電位であり，導線 $ B$ は電位が低くなります．このことは電池の正端子と負端子の関係からも理解できますが，電流の向きからも判断できます．電池の中で電位差が生じているのは化学エネルギーのためであり，抵抗に電位差があるのは一様な電場のためです．（抵抗は導体ですが，電流が流れている状態では電位差が生じていて等電位ではありません．）導線 $ A$ と導線 $ B$ の電位差は電池と抵抗で同じです．それは等電位である導線 $ A$ と等電位である導線 $ B$ の電位差だからです．このことを，通常，電池の電圧が抵抗にかかっていると表現します．（電圧と電位差は同じことを意味する用語です．）また，鍵3のオームの法則が成立していることは明らかです．

　次に直列回路について成立する関係式を，3つの鍵から導いてみましょう．

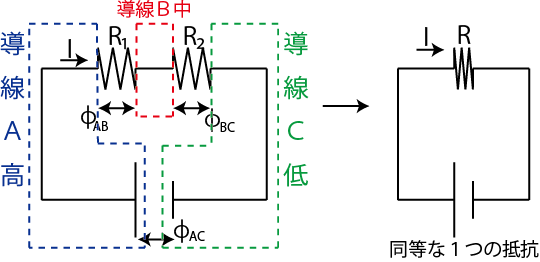
電流回路2

Figure6.4: 電流回路2

鍵1の電流保存より，

$\displaystyle I=I_{1}=I_{2}$

の関係が成立します．鍵2の電位の関係ですが，導線 $ A$，導線 $ B$，導線 $ C$ はそれぞれ等電位です．したがって，

$\displaystyle \phi_{AC}=\phi_{AB}+\phi_{BC}$

の関係が成立します．鍵3の関係は，各抵抗について式を立てると，

  $\displaystyle R: \phi_{AC}=RI$    
  $\displaystyle R_{1}: \phi_{AB}=R_{1}I$    
  $\displaystyle R_{2}: \phi_{BC}=R_{2}I$    

となります．これらの式を電位の関係の式に代入して計算します．

  $\displaystyle RI=R_{1}I+R_{2}I$    
% latex2html id marker 942 $\displaystyle \therefore$ $\displaystyle R=R_{1}+R_{2}$    

最後の式が直列回路における抵抗の合成を示す式です．

　それでは，並列回路の関係について考えましょう．

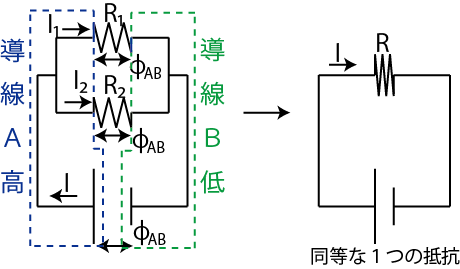
電流回路3

Figure6.5: 電流回路3

鍵1の電流保存ですが，次の関係式が成立します．

$\displaystyle I=I_{1}+I_{2}$

鍵2の電位の関係は，左側の導線 $ A$ は等電位であり，右側の導線 $ B$ も等電位です．したがって，その電位差は抵抗 $ R_{1}$ と抵抗 $ R_{2}$，それに電池で同じになります．そして，その電位差を $ \phi_{AB}[V]$ とします．鍵3のオームの法則は，各抵抗について次の関係が成立します．

  $\displaystyle R: \phi_{AB}=RI$    
  $\displaystyle R_{1}: \phi_{AB}=R_{1}I_{1}$    
  $\displaystyle R_{2}: \phi_{AB}=R_{2}I_{2}$    

したがって，

  $\displaystyle I=\dfrac{\phi_{AB}}{R}$    
  $\displaystyle I_{1}=\dfrac{\phi_{AB}}{R_{1}}$    
  $\displaystyle I_{2}=\dfrac{\phi_{AB}}{R_{2}}$    

と変形して，これらの式を電流保存の式に代入して計算します．

  $\displaystyle \dfrac{\phi_{AB}}{R}=\dfrac{\phi_{AB}}{R_{1}}+\dfrac{\phi_{AB}}{R_{2}}$    
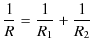% latex2html id marker 967 $\displaystyle \therefore$ $\displaystyle \dfrac{1}{R}=\dfrac{1}{R_{1}}+\dfrac{1}{R_{2}}$    

最後の式が並列回路における抵抗の合成を表す式になります．

 

6.4 コンデンサーと抵抗が混在する回路

コンデンサーと抵抗が混在する回路では，3つの鍵の次の対応を考えるとよいです．

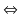  1. 電荷保存 $ \Leftrightarrow$ 電流保存
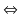  2. 電位の関係 $ \Leftrightarrow$ 電位の関係
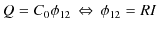
  3. $ Q=C_{0}\phi_{12}\,\Leftrightarrow\,\phi_{12}=RI$

コンデンサー回路と電流回路は電荷と電流の違いはありますが，電場と電位の関係はよく似ています．例えば，最も簡単なコンデンサー回路（コンデンサー1個と電池1個からなる回路）と最も簡単な電流回路（抵抗1個と電池1個からなる回路）では，共にコンデンサー内または抵抗内の一様な電場によって電位差が生じています．導線部分は電流が流れなくても，流れても等電位であり，コンデンサーまたは抵抗の電位差と電池の電位差は同じになります．

 

6.5 ジュール熱

高電位 $ \phi_{2}[V]$ の点から，低電位 $ \phi_{1}[V]$ の点まで，電子 $ -e[C]$ を運ぶとき，外からなすべき仕事 $ W[J]$ は，

$\displaystyle W=e(\phi_{2}-\phi_{1})=e\phi_{12}$

となります．強さ $ I[A]$ の電流は単位時間当たり $ I[C]$ の電荷を運びますので，上記の2点間で，

$\displaystyle P=I\phi_{12}$

の仕事を単位時間当たりにすることになります．オームの法則を使うと，

$\displaystyle P=I\phi_{12}$ $\displaystyle =I\cdot RI=RI^{2}$    
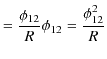  $\displaystyle =\dfrac{\phi_{12}}{R}\phi_{12}=\dfrac{\phi_{12}^{2}}{R}$    

とも表せます．この仕事がジュール熱として発生することになります．

　以上のことを微視的に取り扱ってみましょう．電荷 $ -e[C]$ の電子は電場から $ e\vec{E}[N]$ の力を受けながら，時間 $ \Delta t[s]$ の間に，速度を $ \vec{v}[m/s]$ として， $ \vec{v}\cdot\Delta t[m]$ だけ動きます．したがって，この間，電場は電子に対して，

$\displaystyle \Delta W=e\vec{E}\cdot\vec{v}\Delta t$

の仕事をします．電子はこれだけの仕事を受けながら等速運動を続けて，運動エネルギーは増加しません．そして，全て熱エネルギーに変わります．単位体積中の電子の数を $ n[$個$ /m^{3}]$ として，単位時間に単位体積中で発生する熱は，

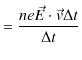$\displaystyle \dfrac{n\Delta W}{\Delta t}$ $\displaystyle =\dfrac{ne\vec{E}\cdot\vec{v}\Delta t}{\Delta t}$    
  $\displaystyle =\vec{E}\cdot en\vec{v}$    
  $\displaystyle =\vec{E}\cdot\vec{i}\,$    

すなわち，

$\displaystyle P=\vec{E}\cdot\vec{i}\,$

となります．これが，ジュール熱を微視的に表した式です．