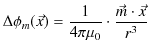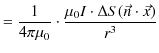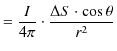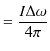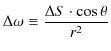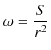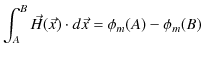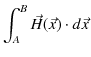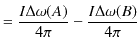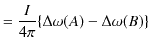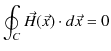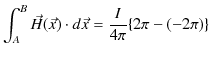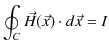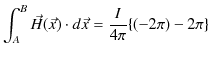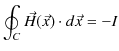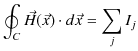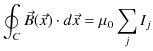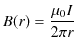Chapter9 定常電流の静磁場(ビオ-サバールの法則とアンペールの法則)
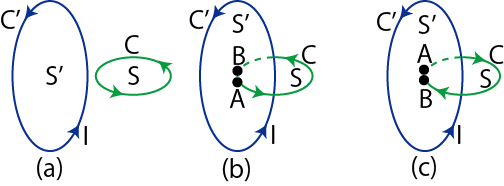
9.1 定常電流の静磁場の3つの例
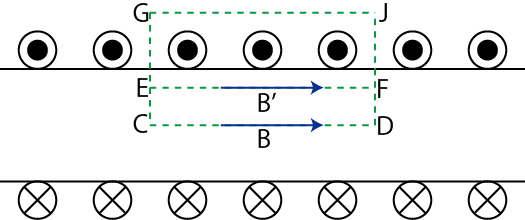
定常電流が流れるとその周りに静磁場が生じます.幾つかの簡単な場合について,それぞれ成立する実験式を見ておきましょう.第一の例として無限に長い直線定常電流 ![$ I[A]$](ja_Chapter9_StaticMagneticFieldOfStationaryElectricCurrent_..._images/img1.png) のつくる静磁場を挙げます.静磁場は直線定常電流を中心として同心円状をなし,定常電流の進む向きをねじの進む向きにして,右にねじった向きに生じます.(これを右ねじの法則といいます.)そのときの静磁場の強さ
のつくる静磁場を挙げます.静磁場は直線定常電流を中心として同心円状をなし,定常電流の進む向きをねじの進む向きにして,右にねじった向きに生じます.(これを右ねじの法則といいます.)そのときの静磁場の強さ ![$ H(r)[A/m]$](ja_Chapter9_StaticMagneticFieldOfStationaryElectricCurrent_..._images/img2.png) は,
は,
で表されます.ただし,![$ r[m]$](ja_Chapter9_StaticMagneticFieldOfStationaryElectricCurrent_..._images/img4.png) は直線定常電流からの距離です.
は直線定常電流からの距離です.
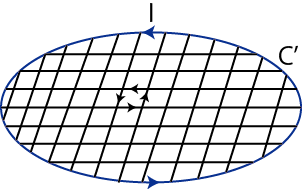
第二の例として,円形定常電流 ![$ I[A]$](ja_Chapter9_StaticMagneticFieldOfStationaryElectricCurrent_..._images/img1.png) のつくる静磁場を挙げます.この場合,生じる静磁場は向きも強さも各点で異なっていて複雑です.しかし,円の中心では,静磁場の向きは円を含む面に垂直であり,静磁場の強さ
のつくる静磁場を挙げます.この場合,生じる静磁場は向きも強さも各点で異なっていて複雑です.しかし,円の中心では,静磁場の向きは円を含む面に垂直であり,静磁場の強さ ![$ H(r)[A/m]$](ja_Chapter9_StaticMagneticFieldOfStationaryElectricCurrent_..._images/img2.png) は,円形定常電流の半径を
は,円形定常電流の半径を ![$ r[m]$](ja_Chapter9_StaticMagneticFieldOfStationaryElectricCurrent_..._images/img4.png) として,
として,
と表されます.右手で円形定常電流を握り,中指の向きが定常電流の向きとすると,親指の向きが静磁場の向きになります.
第三の例として,無限に長いソレノイドコイルに流れる定常電流 ![$ I[A]$](ja_Chapter9_StaticMagneticFieldOfStationaryElectricCurrent_..._images/img1.png) のつくる静磁場を挙げます.導線を円筒状に密に巻いたソレノイドに定常電流を流したとき,ソレノイドの内部につくる静磁場は,ソレノイドの軸に平行で強さはどこでもほぼ同じになります.このように,各点の静磁場の向きと大きさが等しい静磁場を一様な静磁場といいます.右手でソレノイドを握り,中指の向きが定常電流の向きとすると,親指の向きが静磁場の向きになります.一様な静磁場の強さ
のつくる静磁場を挙げます.導線を円筒状に密に巻いたソレノイドに定常電流を流したとき,ソレノイドの内部につくる静磁場は,ソレノイドの軸に平行で強さはどこでもほぼ同じになります.このように,各点の静磁場の向きと大きさが等しい静磁場を一様な静磁場といいます.右手でソレノイドを握り,中指の向きが定常電流の向きとすると,親指の向きが静磁場の向きになります.一様な静磁場の強さ ![$ H[A/m]$](ja_Chapter9_StaticMagneticFieldOfStationaryElectricCurrent_..._images/img6.png) は,ソレノイドの太さに関係なく,
は,ソレノイドの太さに関係なく,
で表されます.ただし,![$ n[1/m]$](ja_Chapter9_StaticMagneticFieldOfStationaryElectricCurrent_..._images/img8.png) は長さ
は長さ ![$ 1[m]$](ja_Chapter9_StaticMagneticFieldOfStationaryElectricCurrent_..._images/img9.png) 当たりの導線の巻き数です.
当たりの導線の巻き数です.
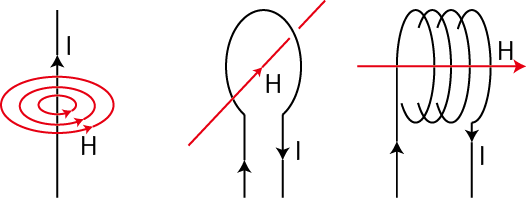
Figure9.1: 3つの例
9.3 磁気双極子
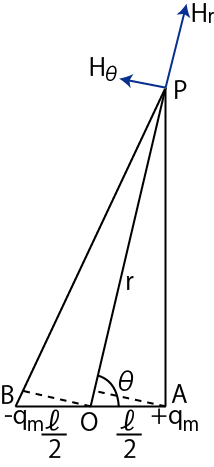
"静電位" のChapterの "電気双極子" のSectionの議論を思い出しましょう.電気双極子の中心からの距離 ![$ r[m]$](ja_Chapter9_StaticMagneticFieldOfStationaryElectricCurrent_..._images/img4.png) ,なす角
,なす角
![$ \theta[rad]$](ja_Chapter9_StaticMagneticFieldOfStationaryElectricCurrent_..._images/img83.png) の位置における静電位
の位置における静電位 ![$ \phi[V]$](ja_Chapter9_StaticMagneticFieldOfStationaryElectricCurrent_..._images/img84.png) は次式で表されました.ただし,2つの静電荷は
は次式で表されました.ただし,2つの静電荷は ![$ \pm q[C]$](ja_Chapter9_StaticMagneticFieldOfStationaryElectricCurrent_..._images/img85.png) ,静電荷間の距離は
,静電荷間の距離は ![$ \ell[m]$](ja_Chapter9_StaticMagneticFieldOfStationaryElectricCurrent_..._images/img86.png) です.
です.
ここで,大きさを
![$ p[C\cdot m]$](ja_Chapter9_StaticMagneticFieldOfStationaryElectricCurrent_..._images/img88.png) ,向きを負電荷から正電荷に向かう方向としたベクトルを電気双極子モーメント
,向きを負電荷から正電荷に向かう方向としたベクトルを電気双極子モーメント
![$ \vec{p}[C\cdot m]$](ja_Chapter9_StaticMagneticFieldOfStationaryElectricCurrent_..._images/img89.png) といいました.電位から
といいました.電位から 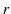 方向と
方向と 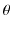 方向の静電場を求めると次のようになりました.
方向の静電場を求めると次のようになりました.
また,電気双極子による静電位は,スカラー積を使うと次のように書き直すことができます.
この式から,静電場は,
とも表されます.
したがって,電気双極子のつくる静電場を表す式と全く同様に,磁気双極子のつくる静磁場は,
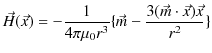 |
(9.3) |
とも表されます.
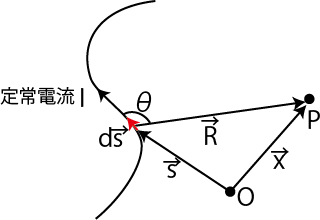
以上の議論は,ペアとなる静磁荷により磁気双極子を形成した場合です.磁気双極子を形成するもう一つの方法として,閉じた定常電流を考えることができます.ここでは特別な例として,一辺の微小な長さ ![$ a[m]$](ja_Chapter9_StaticMagneticFieldOfStationaryElectricCurrent_..._images/img108.png) の正方形の4辺の上を流れる定常電流を取り扱い,ビオ-サバールの法則(9.1)式,
の正方形の4辺の上を流れる定常電流を取り扱い,ビオ-サバールの法則(9.1)式,
より,その電流回路がつくる静磁場を求めてみましょう.
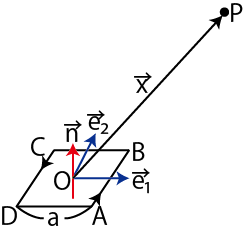
Figure9.6: 磁気双極子2
図のように正方形の回路を 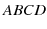 とし,辺
とし,辺 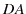 と辺
と辺 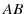 に平行な単位ベクトルを
に平行な単位ベクトルを
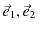 とします.また,正方形の法線ベクトルを
とします.また,正方形の法線ベクトルを 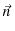 とします.各電流素片が点
とします.各電流素片が点 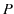 につくる磁束密度は,それぞれ次のようになります.
につくる磁束密度は,それぞれ次のようになります.
ここで,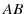 について,
について,
なので(ただし,
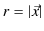 ),
),
となります.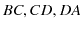 についても同様です.したがって,各電流素片がつくる磁束密度の和は次のようになります.
についても同様です.したがって,各電流素片がつくる磁束密度の和は次のようになります.
ここで,最後の式の 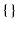 の中を
の中を 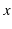 成分について計算します.
成分について計算します.
となります.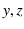 成分の同様なので,
成分の同様なので,
となります.ここで,最後の式の 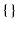 の中を
の中を 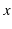 成分について計算します.
成分について計算します.
となります.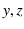 成分も同様なので,
成分も同様なので,
となります.ここで,微小な正方形の面積を,
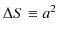 とおきます.このとき,
とおきます.このとき,
となります.よって,静磁場は,
となります.ここで,2つの静磁荷がペアになっている磁気双極子のつくる静磁場の(9.3)式と見比べてみると,磁気双極子モーメントが,
に相当していることがわかります.つまり,閉じた正方形の電流回路も磁気双極子の役割をしているのです.このときの静磁場は,
となり,前述の2つの静磁荷がペアになっている磁気双極子の場合の(9.3)式と完全に一致します.したがって,閉じた電流回路も磁気双極子と呼ぶことにします.また,上に述べたのは正方形の閉回路の場合でしたが,円形電流,長方形の電流等,閉回路一般について磁気双極子モーメントの式は成立することがわかっています.
![]() がつくる磁気双極子の磁位は電気双極子の場合と全く同じ計算により,次式のようになります.
がつくる磁気双極子の磁位は電気双極子の場合と全く同じ計算により,次式のようになります.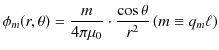
![]() ,向きを負磁荷から正磁荷に向かう方向としたベクトルを磁気双極子モーメント
,向きを負磁荷から正磁荷に向かう方向としたベクトルを磁気双極子モーメント
![]() といいます.静磁位から
といいます.静磁位から ![]() 方向と
方向と ![]() 方向の静磁場を求めると次のようになります.
方向の静磁場を求めると次のようになります.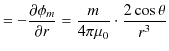
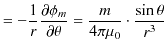
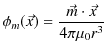
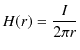
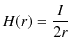

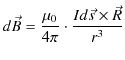
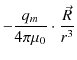
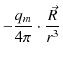
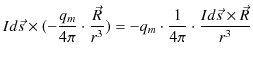
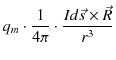
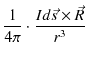
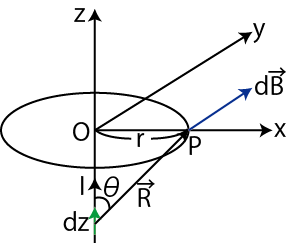
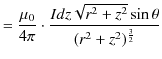
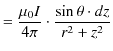
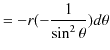
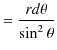
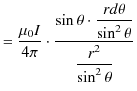
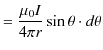
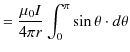
![$\displaystyle =\dfrac{\mu_{0}I}{4\pi r}[-\cos\theta]_{0}^{\pi}$](ja_Chapter9_StaticMagneticFieldOfStationaryElectricCurrent_..._images/img49.png)
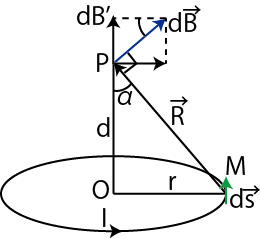
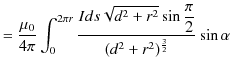
![$\displaystyle =\dfrac{\mu_{0}}{4\pi}\dfrac{I}{d^{2}+r^{2}}[s]_{0}^{2\pi r}\sin\alpha$](ja_Chapter9_StaticMagneticFieldOfStationaryElectricCurrent_..._images/img62.png)
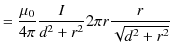
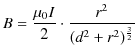
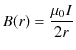
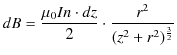
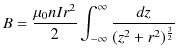
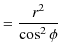
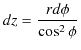
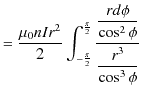

![$\displaystyle =\dfrac{\mu_{0}nI}{2}[\sin\phi]_{-\frac{\pi}{2}}^{\frac{\pi}{2}}$](ja_Chapter9_StaticMagneticFieldOfStationaryElectricCurrent_..._images/img81.png)
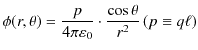
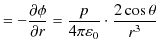
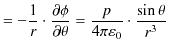
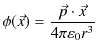
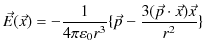
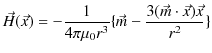

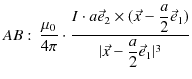
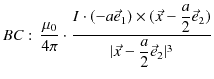
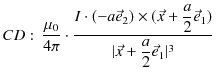
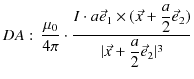
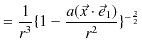
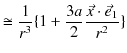
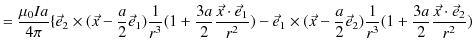
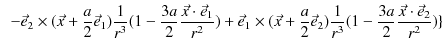
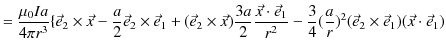
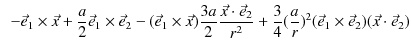
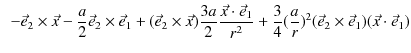
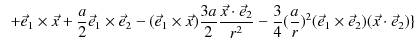
![$\displaystyle =\dfrac{\mu_{0}Ia}{4\pi r^{3}}[a(-\vec{e}_{2}\times\vec{e}_{1}+\v...
...\vec{x}\cdot\vec{e}_{1})-(\vec{e}_{1}\times\vec{x})(\vec{x}\cdot\vec{e}_{2})\}]$](ja_Chapter9_StaticMagneticFieldOfStationaryElectricCurrent_..._images/img135.png)
![$\displaystyle =\dfrac{\mu_{0}Ia^{2}}{4\pi r^{3}}[2\vec{e}_{1}\times\vec{e}_{2}+...
...}(\vec{x}\cdot\vec{e}_{2})+\vec{e}_{2}(\vec{x}\cdot\vec{e}_{1})\}\times\vec{x}]$](ja_Chapter9_StaticMagneticFieldOfStationaryElectricCurrent_..._images/img136.png)
![$\displaystyle =\dfrac{\mu_{0}Ia^{2}}{4\pi r^{3}}[2\vec{e}_{1}\times\vec{e}_{2}+\dfrac{3}{r^{2}}\{(\vec{e}_{1}\times\vec{e}_{2})\times\vec{x}\}\times\vec{x}]$](ja_Chapter9_StaticMagneticFieldOfStationaryElectricCurrent_..._images/img146.png)
![$\displaystyle =\dfrac{\mu_{0}Ia^{2}}{4\pi r^{3}}[2\vec{n}+\dfrac{3}{r^{2}}\{(\vec{n}\times\vec{x})\times\vec{x}\}]$](ja_Chapter9_StaticMagneticFieldOfStationaryElectricCurrent_..._images/img147.png)
![$\displaystyle =\dfrac{\mu_{0}Ia^{2}}{4\pi r^{3}}[2\vec{n}+\dfrac{3}{r^{2}}\{(\vec{n}\cdot\vec{x})\vec{x}-r^{2}\vec{n}\}]$](ja_Chapter9_StaticMagneticFieldOfStationaryElectricCurrent_..._images/img152.png)
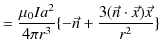
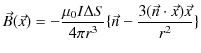
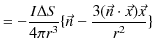
![$\displaystyle =-\dfrac{1}{4\pi\mu_{0}r^{3}}[(\mu_{0}I\cdot\Delta S\cdot\vec{n})-\dfrac{3\{\mu_{0}I\cdot\Delta S(\vec{n}\cdot\vec{x})\}\vec{x}}{r^{2}}]$](ja_Chapter9_StaticMagneticFieldOfStationaryElectricCurrent_..._images/img158.png)
![$\displaystyle \vec{H}(\vec{x})=-\dfrac{1}{4\pi\mu_{0}r^{3}}[\vec{m}-\dfrac{3(\vec{m}\cdot\vec{x})\vec{x}}{r^{2}}]$](ja_Chapter9_StaticMagneticFieldOfStationaryElectricCurrent_..._images/img160.png)