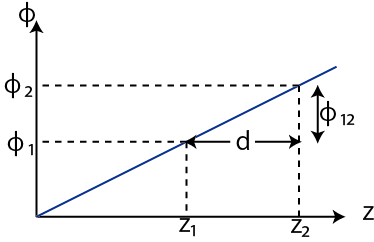
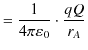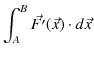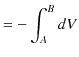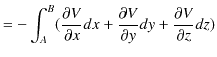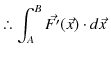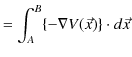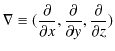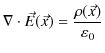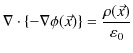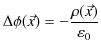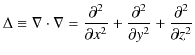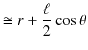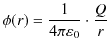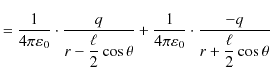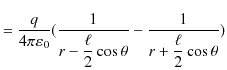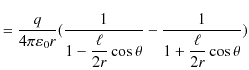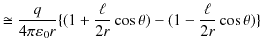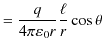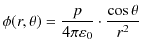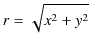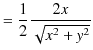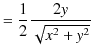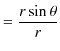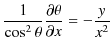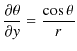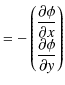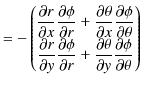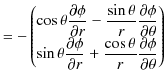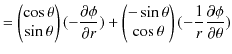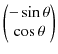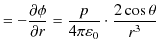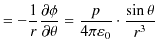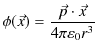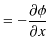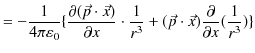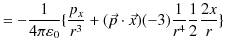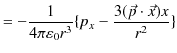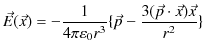ここで,無限遠をポテンシャルの基準として,
![]() としています.また,点電荷
としています.また,点電荷 ![]() から
から ![]() までの距離
までの距離 ![]() を,任意の距離として
を,任意の距離として ![]() とおき直すと,ポテンシャルは次式になります.
とおき直すと,ポテンシャルは次式になります.
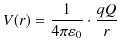
この式を,![]() の重みと,残りの高さを表す量,すなわち静電位
の重みと,残りの高さを表す量,すなわち静電位
![]() に分解します.(
に分解します.(
![]() .)ここで,
.)ここで,
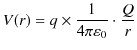
より,静電位
![]() は次式になります.
は次式になります.
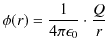
この式は,点電荷 ![]() が負の場合も自動的に含んでいます.静電位
が負の場合も自動的に含んでいます.静電位
![]() と距離
と距離 ![]() の関係をグラフに描くと図 "静電位2" のようになります.
の関係をグラフに描くと図 "静電位2" のようになります.
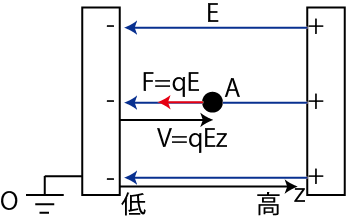
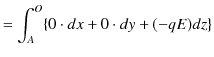
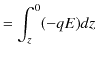
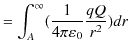
![$\displaystyle =\dfrac{qQ}{4\pi\varepsilon_{0}}[-\dfrac{1}{r}]_{A}^{\infty}$](ja_Chapter3_StaticElectricPotential_images/img29.png)