J Simplicity 導体と静電場

Chapter4 導体と静電場

4.1 静電誘導

導体とは，電気を伝導する物質のことをいいます．電気を伝導しない物質は，不導体（絶縁体，誘電体）といいます．導体の代表例は金属が挙げられます．

　導体には静電誘導という現象が起こります．これは，帯電体を導体に近づけたとき，導体の帯電体に近い側の端に帯電体と異符号の電荷が現れ，遠い側の端に帯電体と同符号の電荷が現れる現象です．導体が金属の場合，静電誘導の原因は自由電子の移動によるものです．静電誘導が起こると引力が働くことになります．

静電誘導

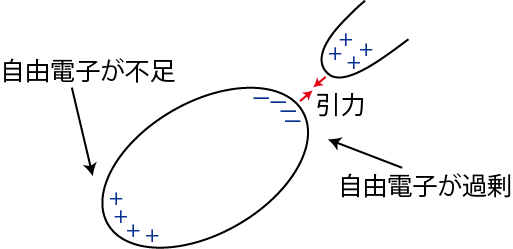
Figure4.1: 静電誘導

4.2 導体の性質

導体は金属等，どこにでもあるようなありふれた物質ですが，電気的に幾つかの特徴のある性質をもっています．電荷の分布や電場が時間的に変化しない状態において，導体の性質として，次の4つが挙げられます．

導体内部の静電場はです．
マクロに見れば導体内部に静電荷は存在しません．
導体の内部，表面は等電位です．
導体の外部の電気力線は導体表面と垂直に交わります．

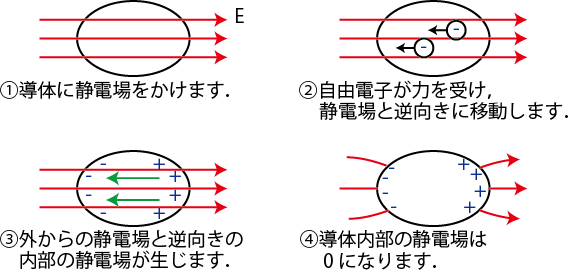
導体内部の静電場0

Figure4.2: 導体内部の静電場0

図のように，導体内部の静電場はになります．もし，静電場が少しでも残っていれば，自由電子が力を受け，静電場と逆向きに移動し，静電場を完全に打ち消します．最終的には静電場はに落ち着き，自由電子の移動は止まります．また，導体内部に静電荷が存在すれば，その静電荷が静電場を生じますので，静電場ということと矛盾します．したがって，静電荷は内部に入り込めません．表面に分布します．そして，静電場がということから，静電場と静電位の関係を考えると，静電位についての導体の特徴を理解することができます．つまり，静電場がのとき，高い低いということがありませんので，静電位に差がない，つまり等電位になるのです．この性質は，後のSectionで見るように，コンデンサー回路において決定的な役割をします．最後に，電気力線と等電位面は直交しますので，4番目の性質が成立します．

4.3 コンデンサー

任意の形状をした2つの導体を接近させておき，1つの導体を正に，もう1つの導体を負に帯電させると，正と負の静電荷はお互いに引き合います．この状態を静電荷が充電されたものと考えることができますが，この系をコンデンサーといいます．

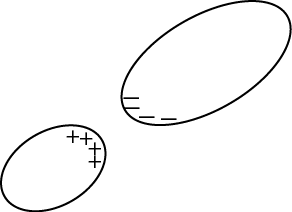
コンデンサー1

Figure4.3: コンデンサー1

特に，2枚の平行な導体板からできているコンデンサーを平行板コンデンサーといいます．平行板コンデンサーが充電されているとき，極板間には一様な静電場ができています．また，今後，単にコンデンサーといった場合，平行板コンデンサーのことを意味することにします．コンデンサーに電池を接続した瞬間から，コンデンサーには充電が開始されます．コンデンサーに充電され始める瞬間は，最大の電流が流れ，コンデンサーは導線と同等の働きをします．その後，徐々に電流は小さくなり，充電が完了した後は，電流は流れなくなり，コンデンサーは不導体の働きをします．次に，充電完了したコンデンサーを電池から切り離し，抵抗に接続するとコンデンサーから電流が流れ出します．これをコンデンサーの放電といいます．放電が終わると，コンデンサーには静電荷がなくなります．

　ここで，このChapterで述べるコンデンサーおよびコンデンサー回路と，電流のChapterで述べる電流および電流回路は，（静）電荷，静電場，静電位の3つの基礎概念によって根本的に理解することができることに注意しましょう．コンデンサー，コンデンサー回路，電流，電流回路は（静）電荷，静電場，静電位の概念についての演習問題と思っていただいて差し支えありません．

　さて，電荷が蓄えられている極板面積 $S[m^{2}]$ ，極板間隔の平行板コンデンサーの極板間の電位差が $\phi_{12}[V]$ の場合，これらの量の間に成立する関係を導いてみましょう．ただし，平行板コンデンサー間の静電場は一様な静電場です．（コンデンサーには静電荷があるので静電場が生じています．静電場があるので静電位に差ができます．この電位差は "静電位" のChapterに出てきた電位差の概念と同一のものになります．）

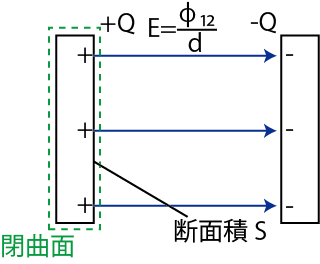
コンデンサー2

Figure4.4: コンデンサー2

まず，ガウスの法則，

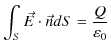
$\displaystyle \int_{S}\vec{E}\cdot\vec{n}dS=\dfrac{Q}{\varepsilon_{0}}$

を図の緑の閉曲面に適用します．

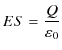	$\displaystyle ES=\dfrac{Q}{\varepsilon_{0}}$
$% latex2html id marker 786 $\displaystyle \therefore$$	$\displaystyle Q=\varepsilon_{0}ES$

となります．ここで，関係式，

$\displaystyle E=\dfrac{\phi_{12}}{d}$

より，

	$\displaystyle Q=\varepsilon_{0}\dfrac{\phi_{12}}{d}S$
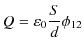$% latex2html id marker 791 $\displaystyle \therefore$$	$\displaystyle Q=\varepsilon_{0}\dfrac{S}{d}\phi_{12}$

となります．右辺に出てくる量を，

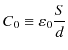
$\displaystyle C_{0}\equiv\varepsilon_{0}\dfrac{S}{d}$

として，電気容量 $C_{0}$ を定義すると，

$\displaystyle Q=C_{0}\phi_{12}$

が成立し，蓄えられる静電荷は極板間の電位差 $\phi_{12}[V]$ に比例することがわかります．電気容量 $C_{0}[F]$ は静電荷の溜まりやすさを表し，単位はです．

4.4 コンデンサー回路

コンデンサー回路の問題解決において根本的な関係は，次に示す "コンデンサー回路を解く３つの鍵" です．

電荷保存
静電位の関係
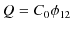
関係式: $Q=C_{0}\phi_{12}$

鍵1の電荷保存においては，他の導体に接触していない孤立導体を探して，それに電荷保存の法則を適用します．鍵2の静電位の関係においては，導体の性質のSectionで説明したように，孤立導体が等電位であることを使います．ここで，並列回路，直列回路において成立する関係式は，この3つの鍵を用いて導くことができることに注意しましょう．また，複雑なコンデンサー回路でも，ほとんどの場合，この3つの鍵を考えれば解決することができます．

　それでは，最も簡単なコンデンサー回路から話を始めましょう．最も簡単なコンデンサー回路とは，図のようにコンデンサーが1個と電池が1個だけから構成される回路です．

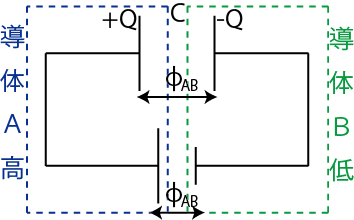
コンデンサー回路1

Figure4.5: コンデンサー回路1

図のように，左側の導体と右側の導体に分けて考えます．電池の部分は電解質溶液で満たされているので電荷は移動することができますが，電位差があるので静電位の上では左側の導体と右側の導体に分けて考えることにします．鍵1の電荷保存に関しては，この場合使用しません．鍵2の電位の関係について言及しておきます．導体の第3の性質，すなわち孤立導体は等電位であるというものから，導体と導体はそれぞれ等電位になっています．導体の方が高電位であり，導体は静電位が低い状態です．これは電池の正端子と負端子の関係からも理解できますが，コンデンサーが正に帯電している導体の方が高電位であり，負に帯電している導体の方が低電位であると把握することもできます．電池の中で電位差が生じているのは化学エネルギーのためであり，コンデンサー間に電位差があるのは一様な静電場の存在のためです．導体の電位と導体の静電位の差は電池とコンデンサーで同じになります．その理由は等電位である導体と等電位である導体の電位差が電池の部分とコンデンサーの部分で等しいからです．このことを，通常，電池の電圧がコンデンサーにかかっていると表現します．（電圧と電位差はほとんど同じ意味の用語です．）また，鍵3の関係式が成立することはいうまでもありません．

　次に並列回路について成立する関係式を3つの鍵から導いておきましょう．

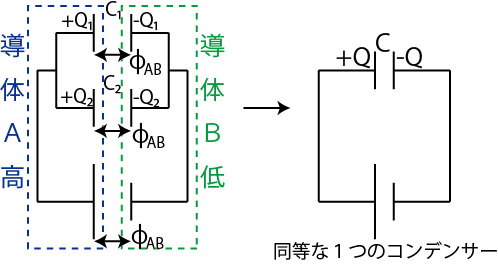
コンデンサー回路2

Figure4.6: コンデンサー回路2

鍵1の電荷保存はこの場合使用しません．静電荷の関係としては，2つのコンデンサーと同等な1つのコンデンサーを考えたとき，

$\displaystyle Q=Q_{1}+Q_{2}$

が成立します．鍵2の静電位の関係は，左側の導体は等電位であり，右側の導体も等電位です．したがって，その電位差はコンデンサー $C_{1}$ とコンデンサー $C_{2}$ ，それに電池で同じになります．そして，その電位差を $\phi_{AB}[V]$ とします．鍵3の関係は，各コンデンサーに次の関係が成立します．

	$\displaystyle Q=C\phi_{AB}$
	$\displaystyle Q_{1}=C_{1}\phi_{AB}$
	$\displaystyle Q_{2}=C_{2}\phi_{AB}$

これらの式を静電荷の関係の式に代入して計算すると，

	$\displaystyle C\phi_{AB}=C_{1}\phi_{AB}+C_{2}\phi_{AB}$
$% latex2html id marker 862 $\displaystyle \therefore$$	$\displaystyle C=C_{1}+C_{2}$

となります．最後の式が並列回路における電気容量の合成を表す式です．

　直列回路の場合も3つの鍵を用いて取り扱うことができます．

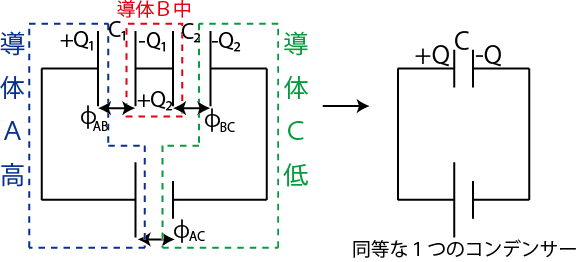
コンデンサー回路3

Figure4.7: コンデンサー回路3

鍵1の電荷保存を孤立導体に適用します．はじめの状態では，孤立導体には電荷がだったので，

	$\displaystyle 0=-Q_{1}+Q_{2}$
$% latex2html id marker 875 $\displaystyle \therefore$$	$\displaystyle Q_{1}=Q_{2}(=Q)$

の関係が成立します．鍵2の静電位の関係ですが，導体，導体，導体はそれぞれ等電位です．したがって，

$\displaystyle \phi_{AC}=\phi_{AB}+\phi_{BC}$

の関係が成立します．鍵3の関係は，各コンデンサーについて式を立てると，

	$\displaystyle C; Q=C\phi_{AC}$
	$\displaystyle C_{1}; Q=C_{1}\phi_{AB}$
	$\displaystyle C_{2}; Q=C_{2}\phi_{BC}$

となります．よって，

$\displaystyle \phi_{AC}$	$\displaystyle =\dfrac{Q}{C}$
$\displaystyle \phi_{AB}$	$\displaystyle =\dfrac{Q}{C_{1}}$
$\displaystyle \phi_{BC}$	$\displaystyle =\dfrac{Q}{C_{2}}$

となります．これらの式を静電位の関係の式に代入して計算します．

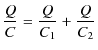	$\displaystyle \dfrac{Q}{C}=\dfrac{Q}{C_{1}}+\dfrac{Q}{C_{2}}$
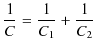$% latex2html id marker 895 $\displaystyle \therefore$$	$\displaystyle \dfrac{1}{C}=\dfrac{1}{C_{1}}+\dfrac{1}{C_{2}}$

最後の式が直列回路における電気容量の合成を表す式です．

4.5 静電エネルギー

充電したコンデンサーは両極を導線でつなげば，放電して仕事をすることができます．したがって，充電したコンデンサーはポテンシャルをもっています．このポテンシャルを静電エネルギーと呼びます．以下に，この静電エネルギーを求めてみます．

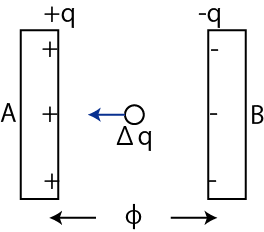
静電エネルギー

Figure4.8: 静電エネルギー

図のように，充電を行わせるために，極板Bから微小量の電荷 $\Delta q[C]$ ずつ極板へ運ぶ状況を考えます．電位差から始めて，ある時刻に電位差が $\phi[V]$ ，静電荷が $\pm q[C]$ の状態になったとします．この状態のとき，さらに $\Delta q[C]$ の電荷を運ぶのに要する仕事 $\Delta W[J]$ は，

$\displaystyle \Delta W=\Delta q\cdot\phi$

となります．ここで，電気容量をとして，

$\displaystyle q=C\phi$

なので，

$\displaystyle \Delta W=C\Delta\phi\cdot\phi$

と表せます．したがって，電位差が $\phi_{AB}[V]$ ，全電荷がになるまでに必要な仕事は，

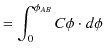$\displaystyle W$	$\displaystyle =\int_{0}^{\phi_{AB}}C\phi\cdot d\phi$
	$\displaystyle =C[\dfrac{1}{2}\phi^{2}]_{0}^{\phi_{AB}}$
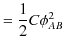	$\displaystyle =\dfrac{1}{2}C\phi_{AB}^{2}$

となりますが，仕事をされた分だけ，静電エネルギーとして蓄えられることになります．故に，静電エネルギーは，

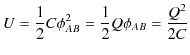
$\displaystyle U=\dfrac{1}{2}C\phi_{AB}^{2}=\dfrac{1}{2}Q\phi_{AB}=\dfrac{Q^{2}}{2C}$

で与えられます．

　この静電エネルギーは蓄えられた静電荷の間に働くクーロン力によるポテンシャルであると考えると，静電荷が遠く隔たったまま力が働く遠隔作用の立場になります．しかし，``静電場（ガウスの法則）'' のChapterで見たように，クーロン力は空間の歪みである静電場から受けるのであって，近接作用の立場から考えなければなりません．したがって，静電エネルギーも近接作用の観点から考えなおし，エネルギーは空間の歪みである静電場に溜まっているとします．この立場から，静電エネルギーの式を書き直します．空間が真空の場合，平行板コンデンサーの電気容量は，

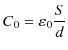
$\displaystyle C_{0}=\varepsilon_{0}\dfrac{S}{d}$

でした．ただし， $\varepsilon_{0}[F/m]$ は真空の誘電率， $S[m^{2}]$ は極板の面積，は極板間隔です．故に，静電エネルギーは，

$\displaystyle U$	$\displaystyle =\dfrac{Q^{2}}{2C}$
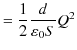	$\displaystyle =\dfrac{1}{2}\dfrac{d}{\varepsilon_{0}S}Q^{2}$
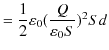	$\displaystyle =\dfrac{1}{2}\varepsilon_{0}(\dfrac{Q}{\varepsilon_{0}S})^{2}Sd$

となります．ここで，ガウスの法則（積分形），

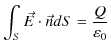
$\displaystyle \int_{S}\vec{E}\cdot\vec{n}dS=\dfrac{Q}{\varepsilon_{0}}$

を平行板コンデンサーに適用すると，

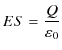	$\displaystyle ES=\dfrac{Q}{\varepsilon_{0}}$
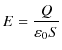$% latex2html id marker 951 $\displaystyle \therefore$$	$\displaystyle E=\dfrac{Q}{\varepsilon_{0}S}$

となります．故に，静電エネルギーは静電場を使って，

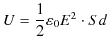
$\displaystyle U=\dfrac{1}{2}\varepsilon_{0}E^{2}\cdot Sd$

となります．ここで， $Sd[m^{3}]$ は平行板コンデンサーの体積なので，単位体積当たりの静電エネルギー $u[J/m^{3}]$ は，

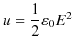
$\displaystyle u=\dfrac{1}{2}\varepsilon_{0}E^{2}$

となります．これが，近接作用による静電エネルギーを表した式です．