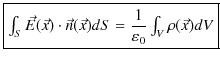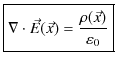Chapter2 静電場（ガウスの法則）

2.1 電場の概念と近接作用

二つの電荷の間には，

$\displaystyle F=k_{0}\dfrac{q_{1}q_{2}}{r^{2}}$

の大きさのクーロン力が働きます．1785年，クーロンにより発見された当時，この力は空間を隔てたまま働き合うと認識されていました．（離れたものが力を及ぼすことを遠隔作用といいます．遠く隔てたままの作用です．）そして，力が働くメカニズムについては何も言及されませんでした．

　ある物理量が空間の場所によって決まるとき，その物理量を場といいます．例えば，物体の場所によって温度がきまるとき，温度場といいます．温度場は大きさだけの場ですので，スカラー場です．また，流体の速度が場所によって決まるとき，速度場といいます．速度場は大きさと向きをもった場ですので，ベクトル場です．以下考えていくように，電気の場のことを電場といいます．電場はベクトル場です．

　クーロンの法則が発見されてから，52年後の1837年，ファラデーは近接作用の概念を導入しました．この概念を用いて，次のようにクーロン力のメカニズムについて，踏み込んで考えましょう．

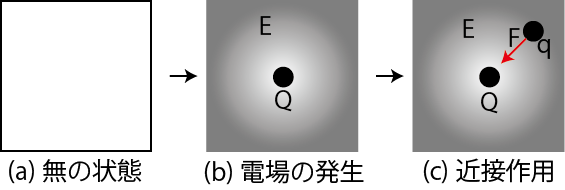
静電場と近接作用

Figure2.1: 静電場と近接作用

電荷が何もないとき，空間には特別なことは起こっていません．（図の(a)無の状態．）ここで，１つだけ電荷 $ Q[C]$ を置きます．そのとき，電荷の周りの空間がある種の緊張状態になります．その状態を電場 $ E$ が生じたと考えるのです．（図の(b)電場の発生．）電場が生じている状態で，もう一つの電荷 $ q[C]$ を置きます．すると，後から置いた電荷 $ q[C]$ は，はじめに置いた電荷 $ Q[C]$ から距離を隔てたまま力を受けるのではなく，空間に生じている電場 $ E$ から力 $ F[N]$ を受けると考えるのです．（図の(c)近接作用．）電荷がすぐ近くの空間から力を受けることを近接作用と言います．例えて説明すると，トランポリンの上に何も載っていないときは電場の無い状態で，そこに重りを置くとトランポリンが窪みますが，それが電場の生じている状態と考えることができます．そのとき，ボールを置くとトランポリンの窪みから（つまり電荷の場合は電場から）力を受けて，ボールは転がることになります．

　クーロンの法則，

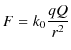
$\displaystyle F=k_{0}\dfrac{qQ}{r^{2}}$

は，そのままでは遠隔作用による表式になっています．この式を変形して，近接作用の概念を式の上で表すことにしましょう．次のように，簡単に変形します．

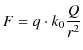
$\displaystyle F=q\cdot k_{0}\dfrac{Q}{r^{2}}$

これだけで，近接作用の式に移行したのです．もっとわかり易くするために，この式で，

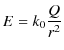
$\displaystyle E=k_{0}\dfrac{Q}{r^{2}}$

とおき，電場を表すと捉えます．これが，最初に置いた $ Q[C]$ の電荷がつくる電場 $ E[N/C]$ です．そうすると，

$\displaystyle F=qE$

という，電場とクーロン力の関係を表した近接作用の概念を表した式になります．すなわち，電荷 $ q[C]$ に作用するクーロン力 $ F[N]$ は，空間に生じている電場 $ E[N/C]$ から働くと認識することができるのです．

　ここで，一様な電場というものに触れておきます．2枚の平行な極板を用意して，それぞれ正と負の電荷を帯電させます．このとき，正と負の電荷の絶対値は等しいものとします．この2枚の極板の間には電場が生じますが，それはどこをとっても同じ大きさ，同じ向きの一様な電場です．この一様な電場 $ E[N/C]$ の中に電荷 $ q[C]$ を置くと，

$\displaystyle F=qE$

の大きさのクーロン力が生じるのです．

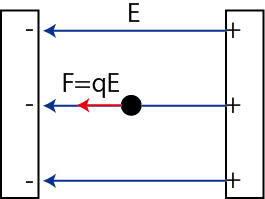
一様な静電場

Figure2.2: 一様な静電場

 

2.2 ガウスの法則

電荷 $ Q[C]$ を中心とする半径 $ R[m]$ の球面を考え，

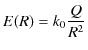
$\displaystyle E(R)=k_{0}\dfrac{Q}{R^{2}}$

の式の両辺に，球の面積 $ 4\pi R^{2}[m^{2}]$ をかけて計算します．

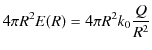  $\displaystyle 4\pi R^{2}E(R)=4\pi R^{2}k_{0}\dfrac{Q}{R^{2}}$    
% latex2html id marker 897 $\displaystyle \therefore$ $\displaystyle 4\pi R^{2}E(R)=4\pi k_{0}Q$    

ここで，真空の誘電率，

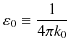
$\displaystyle \varepsilon_{0}\equiv\dfrac{1}{4\pi k_{0}}$

を定義すると，

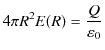
$\displaystyle 4\pi R^{2}E(R)=\dfrac{Q}{\varepsilon_{0}}$

となります．最後の式は，電荷 $ Q[C]$ を中心とする半径 $ R[m]$ の球面上の電場 $ E(R)[N/C]$ に全球面の面積を掛けたものが， $ \frac{Q}{\varepsilon_{0}}[N\cdot m^{2}/C]$ に等しいことを表しています．

　上記のことが，電荷 $ Q[C]$ を囲む任意の閉曲面 $ S$ に対して成立することを証明します．

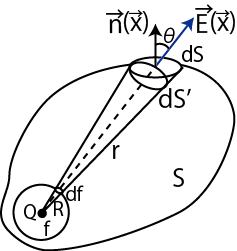
ガウスの法則1

Figure2.3: ガウスの法則1

閉曲面 $ S$ 上の微小面を $ dS[m^{2}]$ とします．$ dS[m^{2}]$ に外向きに立てた法線ベクトル（単位ベクトル）を $ \vec{n}(\vec{x})$ とすると，$ dS[m^{2}]$ 面上の電場 $ \vec{E}(\vec{x})[N/C]$ の $ \vec{n}(\vec{x})$ 方向の成分は，

$\displaystyle \vec{E}(\vec{x})\cdot\vec{n}(\vec{x})$ $\displaystyle =E\cos\theta$    
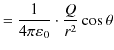  $\displaystyle =\dfrac{1}{4\pi\varepsilon_{0}}\cdot\dfrac{Q}{r^{2}}\cos\theta$    

ここで，$ E[N/C]$ は電場の大きさ，$ r[m]$ は電荷 $ Q[C]$ から微小面 $ dS[m^{2}]$ までの距離， $ \theta[rad]$ は $ \vec{E}(\vec{x})[N/C]$ と $ \vec{n}(\vec{x})$ の間の角度です．このとき，電場 $ \vec{E}(\vec{x})[N/C]$ に垂直な微小面の面積は， $ dS'=dS\cdot\cos\theta$ になります．また，半径 $ R[m]$ の球面上の微小面積 $ df[m^{2}]$ と $ dS'[m^2]$ との比は，

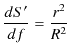
$\displaystyle \dfrac{dS'}{df}=\dfrac{r^{2}}{R^{2}}$

になります．故に，

$\displaystyle \vec{E}(\vec{x})\cdot\vec{n}(\vec{x})dS$ $\displaystyle =E\cos\theta\cdot dS$    
  $\displaystyle =EdS'$    
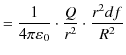  $\displaystyle =\dfrac{1}{4\pi\varepsilon_{0}}\cdot\dfrac{Q}{r^{2}}\cdot\dfrac{r^{2}df}{R^{2}}$    
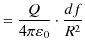  $\displaystyle =\dfrac{Q}{4\pi\varepsilon_{0}}\cdot\dfrac{df}{R^{2}}$    

となります．これを閉曲面 $ S$ 上にわたって面積分すると，

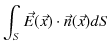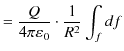$\displaystyle \int_{S}\vec{E}(\vec{x})\cdot\vec{n}(\vec{x})dS$ $\displaystyle =\dfrac{Q}{4\pi\varepsilon_{0}}\cdot\dfrac{1}{R^{2}}\int_{f}df$    
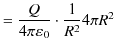  $\displaystyle =\dfrac{Q}{4\pi\varepsilon_{0}}\cdot\dfrac{1}{R^{2}}4\pi R^{2}$    
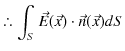% latex2html id marker 972 $\displaystyle \therefore\int_{S}\vec{E}(\vec{x})\cdot\vec{n}(\vec{x})dS$ $\displaystyle =\dfrac{Q}{\varepsilon_{0}}$    

となります．

　次に，電荷 $ Q[C]$ が閉曲面 $ S$ の外側にある場合を考えます．

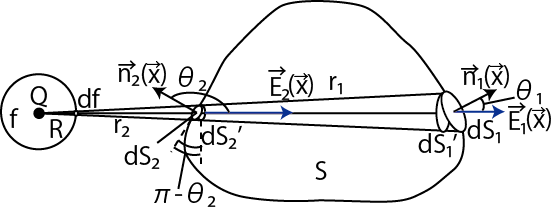
ガウスの法則2

Figure2.4: ガウスの法則2

図より，

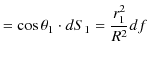$\displaystyle dS'_{1}$ $\displaystyle =\cos\theta_{1}\cdot dS_{1}=\dfrac{r_{1}^{2}}{R^{2}}df$    
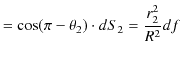$\displaystyle dS'_{2}$ $\displaystyle =\cos(\pi-\theta_{2})\cdot dS_{2}=\dfrac{r_{2}^{2}}{R^{2}}df$    

の関係が成立します．故に，

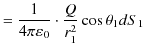$\displaystyle \vec{E}_{1}(\vec{x})\cdot\vec{n}_{1}(\vec{x})dS_{1}$ $\displaystyle =\dfrac{1}{4\pi\varepsilon_{0}}\cdot\dfrac{Q}{r_{1}^{2}}\cos\theta_{1}dS_{1}$    
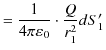  $\displaystyle =\dfrac{1}{4\pi\varepsilon_{0}}\cdot\dfrac{Q}{r_{1}^{2}}dS'_{1}$    
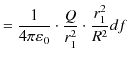  $\displaystyle =\dfrac{1}{4\pi\varepsilon_{0}}\cdot\dfrac{Q}{r_{1}^{2}}\cdot\dfrac{r_{1}^{2}}{R^{2}}df$    
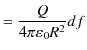  $\displaystyle =\dfrac{Q}{4\pi\varepsilon_{0}R^{2}}df$    

と，

$\displaystyle \vec{E}_{2}(\vec{x})\cdot\vec{n}_{2}(\vec{x})dS_{2}$ $\displaystyle =\dfrac{1}{4\pi\varepsilon_{0}}\cdot\dfrac{Q}{r_{2}^{2}}\cos\theta_{2}dS_{2}$    
  $\displaystyle =-\dfrac{1}{4\pi\varepsilon_{0}}\cdot\dfrac{Q}{r_{2}^{2}}\cos(\pi-\theta_{2})dS_{2}$    
  $\displaystyle =-\dfrac{1}{4\pi\varepsilon_{0}}\cdot\dfrac{Q}{r_{2}^{2}}dS'_{2}$    
  $\displaystyle =-\dfrac{1}{4\pi\varepsilon_{0}}\cdot\dfrac{Q}{r_{2}^{2}}\cdot\dfrac{r_{2}^{2}}{R^{2}}df$    
  $\displaystyle =-\dfrac{Q}{4\pi\varepsilon_{0}R^{2}}df$    

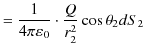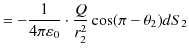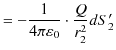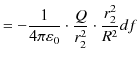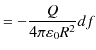となります．従って，

$\displaystyle \vec{E}_{1}(\vec{x})\cdot\vec{n}_{1}(\vec{x})dS_{1}+\vec{E}_{2}(\vec{x})\cdot\vec{n}_{2}(\vec{x})dS_{2}=0$

であり，閉曲面 $ S$ 上にわたる面積分も 0 になります．すなわち，電荷 $ Q[C]$ が閉曲面 $ S$ の外にあるとき，

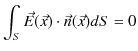
$\displaystyle \int_{S}\vec{E}(\vec{x})\cdot\vec{n}(\vec{x})dS=0$

が成立します．

　議論を一般的にして，閉曲面Sの内部に電荷 $ Q_{1},Q_{2},\cdots,Q_{N}[C]$ があり，外部に電荷 $ q_{a},q_{b},\cdots,q_{z}[C]$ がある場合を考えます．これらの電荷が $ S$ 上の任意の位置につくる電場をそれぞれ， $ \vec{E}_{1}(\vec{x}),\vec{E}_{2}(\vec{x}),\cdots,\vec{E}_{N}(\vec{x}),\vec{E}_{a}(\vec{x}),\vec{E}_{b}(\vec{x}),\cdots,\vec{E}_{z}(\vec{x})[N/C]$ とすると，これらを重ね合わせた全電場 $ \vec{E}(\vec{x})[N/C]$ は，

$\displaystyle \vec{E}(\vec{x})=\vec{E}_{1}(\vec{x})+\cdots+\vec{E}_{N}(\vec{x})+\vec{E}_{a}(\vec{x})+\cdots+\vec{E}_{z}(\vec{x})$

になります．ここで，閉曲面上 $ S$ 全体について，面積分を実行すると，

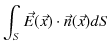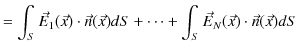$\displaystyle \int_{S}\vec{E}(\vec{x})\cdot\vec{n}(\vec{x})dS$ $\displaystyle =\int_{S}\vec{E}_{1}(\vec{x})\cdot\vec{n}(\vec{x})dS+\cdots+\int_{S}\vec{E}_{N}(\vec{x})\cdot\vec{n}(\vec{x})dS$    
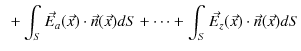  $\displaystyle \,\,\,+\int_{S}\vec{E}_{a}(\vec{x})\cdot\vec{n}(\vec{x})dS+\cdots+\int_{S}\vec{E}_{z}(\vec{x})\cdot\vec{n}(\vec{x})dS$    
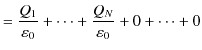  $\displaystyle =\dfrac{Q_{1}}{\varepsilon_{0}}+\cdots+\dfrac{Q_{N}}{\varepsilon_{0}}+0+\cdots+0$    
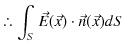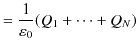% latex2html id marker 1026 $\displaystyle \therefore\int_{S}\vec{E}(\vec{x})\cdot\vec{n}(\vec{x})dS$ $\displaystyle =\dfrac{1}{\varepsilon_{0}}(Q_{1}+\cdots+Q_{N})$    

となります．電荷が空間内のある領域にわたって連続的に分布しているとき，電荷密度（単位体積当たりの電荷）を $ \rho(\vec{x})[C/m^{3}]$ とすると，上式は，

$\displaystyle \fbox{$\int_{S}\vec{E}(\vec{x})\cdot\vec{n}(\vec{x})dS=\dfrac{1}{\varepsilon_{0}}\int_{V}\rho(\vec{x})dV$}$ (2.1)

となります．（右辺は体積分です．）この(2.1)式をガウスの法則（積分形）と言います． ベクトル解析のガウスの定理は，任意のベクトル $ \vec{A}\,$ について，

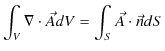
$\displaystyle \int_{V}\nabla\cdot\vec{A}dV=\int_{S}\vec{A}\cdot\vec{n}dS$

と表せます．この定理より，(2.1)式は，

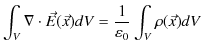
$\displaystyle \int_{V}\nabla\cdot\vec{E}(\vec{x})dV=\dfrac{1}{\varepsilon_{0}}\int_{V}\rho(\vec{x})dV$

と変形されます．この式の両辺のそれぞれの被積分関数は等しくなります．故に，

$\displaystyle \fbox{$\nabla\cdot\vec{E}(\vec{x})=\dfrac{\rho(\vec{x})}{\varepsilon_{0}}$}$ (2.2)

が成立します．この(2.2)式をガウスの法則（微分形）と言います．