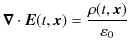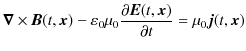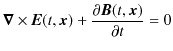Chapter5 特殊相対論的電磁気学

5.1 Maxwell電磁気学

Maxwell電磁気学の根幹をなすものは，次の4式からなるMaxwell方程式でした．

  $\displaystyle \bm{\nabla}\cdot\bm{E}(t,\bm{x})=\dfrac{\rho(t,\bm{x})}{\varepsilon_{0}}$ (5.1)
  $\displaystyle \bm{\nabla}\cdot\bm{B}(t,\bm{x})=0$ (5.2)
  $\displaystyle \bm{\nabla}\times\bm{B}(t,\bm{x})-\varepsilon_{0}\mu_{0}\dfrac{\partial\bm{E}(t,\bm{x})}{\partial t}=\mu_{0}\bm{j}(t,\bm{x})$ (5.3)
  $\displaystyle \bm{\nabla}\times\bm{E}(t,\bm{x})+\dfrac{\partial\bm{B}(t,\bm{x})}{\partial t}=0$ (5.4)

これらの方程式から光速 $ c$ が計算されました．その光速の値 $ c$ は唯一のものです．そして，この事実はGalilei変換に矛盾します．しかし，矛盾してよいのです．特殊相対性理論においては，Galileiの相対性原理は古い理論としての位置付けになるのです．一方，Maxwell方程式はLorentz変換のもとで共変です．従って，Maxwell電磁気学は修正することなく，本質的にそのままで特殊相対論的であるといえるのです．ただし，Lorentz共変性が一目で明らかになるように，4次元的な形式に書き換える必要があります．（修正ではありません書き換えです．本質は変わりません．）特殊相対論的電磁気学を構築するため，この書き換えられた理論を次の Section で見ていきましょう．

 

5.2 Maxwell電磁気学の特殊相対論的書き換え

まず，最初にvector potential $ \bm{A}(t,\bm{x})$ とscalar potential $ \phi(t,\bm{x})$ の定義から見ていきましょう．すなわち，

  $\displaystyle \bm{B}(t,\bm{x})=\bm{\nabla}\times\bm{A}(t,\bm{x})$    
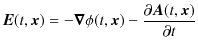  $\displaystyle \bm{E}(t,\bm{x})=-\bm{\nabla}\phi(t,\bm{x})-\dfrac{\partial\bm{A}(t,\bm{x})}{\partial t}$    

の式で定義します．このとき，Maxwell方程式の(5.2)式と(5.4)式は自動的に成立することが，次のように確かめられます．すなわち，

$\displaystyle \bm{\nabla}\cdot\bm{B}(t,\bm{x})$ $\displaystyle =\bm{\nabla}\cdot\{\bm{\nabla}\times\bm{A}(t,\bm{x})\}$    
  $\displaystyle =0$    

と，

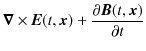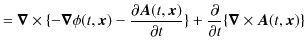$\displaystyle \bm{\nabla}\times\bm{E}(t,\bm{x})+\dfrac{\partial\bm{B}(t,\bm{x})}{\partial t}$ $\displaystyle =\bm{\nabla}\times\{-\bm{\nabla}\phi(t,\bm{x})-\dfrac{\partial\bm... ...\partial t}\}+\dfrac{\partial}{\partial t}\{\bm{\nabla}\times\bm{A}(t,\bm{x})\}$    
  $\displaystyle =-\bm{\nabla}\times\{\bm{\nabla}\phi(t,\bm{x})\}$    
  $\displaystyle =0$    

のようになります．いずれの変形にも，最後にvector解析の公式を使用しました．これらのpotentialから4元vectorを構成します．

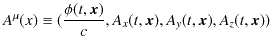  $\displaystyle A^{\mu}(x)\equiv(\dfrac{\phi(t,\bm{x})}{c},A_{x}(t,\bm{x}),A_{y}(t,\bm{x}),A_{z}(t,\bm{x}))$    
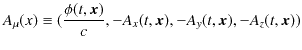  $\displaystyle A_{\mu}(x)\equiv(\dfrac{\phi(t,\bm{x})}{c},-A_{x}(t,\bm{x}),-A_{y}(t,\bm{x}),-A_{z}(t,\bm{x}))$    

ただし，

$\displaystyle x$ $\displaystyle \equiv x^{\mu}$    
  $\displaystyle =(x^{0},x^{1},x^{2},x^{3})$    
  $\displaystyle =(ct,x,y,z)$    
  $\displaystyle =(ct,\bm{x})$    

としておきます．さらに，4元電流密度vectorと4次元の微分演算子を，次のように定義します．

  $\displaystyle j^{\mu}(x)\equiv(c\rho(t,\bm{x}),j_{x}(t,\bm{x}),j_{y}(t,\bm{x}),j_{z}(t,\bm{x}))$    
  $\displaystyle j_{\mu}(x)\equiv(c\rho(t,\bm{x}),-j_{x}(t,\bm{x}),-j_{y}(t,\bm{x}),-j_{z}(t,\bm{x}))$    

と，

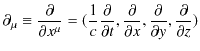  $\displaystyle \partial_{\mu}\equiv\dfrac{\partial}{\partial x^{\mu}}=(\dfrac{1}... ...partial}{\partial x},\dfrac{\partial}{\partial y},\dfrac{\partial}{\partial z})$    
  $\displaystyle \partial^{\mu}\equiv\dfrac{\partial}{\partial x_{\mu}}=(\dfrac{1}... ...rtial}{\partial x},-\dfrac{\partial}{\partial y},-\dfrac{\partial}{\partial z})$    

です．さらに，2階反変tensorを定義します．

$\displaystyle \fbox{$F^{\mu\nu}(x)\equiv\partial^{\mu}A^{\nu}(x)-\partial^{\nu}A^{\mu}(x)$}$ (5.5)

右辺を計算します．

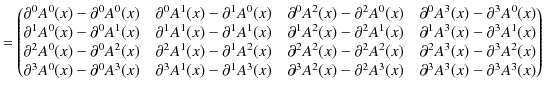$\displaystyle F^{\mu\nu}(x)$ $\displaystyle = \begin{pmatrix} \partial^{0}A^{0}(x)-\partial^{0}A^{0}(x) & \... ...\partial^{2}A^{3}(x) & \partial^{3}A^{3}(x)-\partial^{3}A^{3}(x) \end{pmatrix}$    
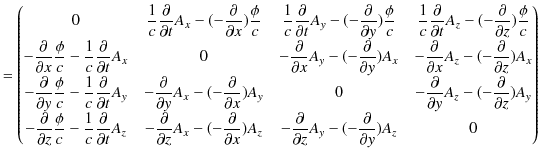  $\displaystyle = \begin{pmatrix} 0 & \dfrac{1}{c}\dfrac{\partial}{\partial t}A... ...rtial}{\partial z}A_{y}-(-\dfrac{\partial}{\partial y})A_{z} & 0 \end{pmatrix}$    
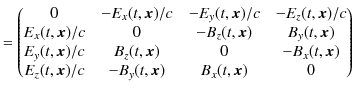  $\displaystyle = \begin{pmatrix} 0 & -E_{x}(t,\bm{x})/c & -E_{y}(t,\bm{x})/c &... ...)\\ E_{z}(t,\bm{x})/c & -B_{y}(t,\bm{x}) & B_{x}(t,\bm{x}) & 0 \end{pmatrix}$    

このとき， $ F^{\mu\nu}(x)$ には $ \bm{A}(t,\bm{x})$ と $ \phi(t,\bm{x})$ が含まれていますので，Maxwell方程式(5.2)式と(5.4)式は自動的に成立します．また，Maxwell方程式(5.1)式と(5.3)式は次式で表されます．

$\displaystyle \fbox{$\partial_{\mu}F^{\mu\nu}(x)=\mu_{0}j^{\nu}(x)$}$ (5.6)

この(5.6)式が，確かに(5.1)式と(5.3)式を表していることを確認しておきます．左辺は，

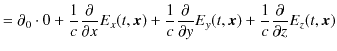$\displaystyle \partial_{0}F^{00}(x)+\partial_{1}F^{10}(x)+\partial_{2}F^{20}(x)+\partial_{3}F^{30}(x)$ $\displaystyle =\partial_{0}\cdot0+\dfrac{1}{c}\dfrac{\partial}{\partial x}E_{x}... ...rtial y}E_{y}(t,\bm{x})+\dfrac{1}{c}\dfrac{\partial}{\partial z}E_{z}(t,\bm{x})$    
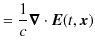  $\displaystyle =\dfrac{1}{c}\bm{\nabla}\cdot\bm{E}(t,\bm{x})$    

ですが，一方右辺は，

$\displaystyle \mu_{0}j^{0}(x)=\mu_{0}(c\rho(t,\bm{x}))$

です．故に，

$\displaystyle \bm{\nabla}\cdot\bm{E}(t,\bm{x})$ $\displaystyle =c^{2}\mu_{0}\rho(t,\bm{x})$    
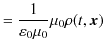  $\displaystyle =\dfrac{1}{\varepsilon_{0}\mu_{0}}\mu_{0}\rho(t,\bm{x})$    
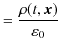  $\displaystyle =\dfrac{\rho(t,\bm{x})}{\varepsilon_{0}}$    

となります．これは，(5.1)式です．また，

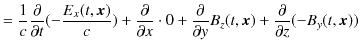$\displaystyle \partial_{0}F^{01}(x)+\partial_{1}F^{11}(x)+\partial_{2}F^{21}(x)+\partial_{3}F^{31}(x)$ $\displaystyle =\dfrac{1}{c}\dfrac{\partial}{\partial t}(-\dfrac{E_{x}(t,\bm{x})... ...tial}{\partial y}B_{z}(t,\bm{x})+\dfrac{\partial}{\partial z}(-B_{y}(t,\bm{x}))$    
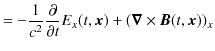  $\displaystyle =-\dfrac{1}{c^{2}}\dfrac{\partial}{\partial t}E_{x}(t,\bm{x})+(\bm{\nabla}\times\bm{B}(t,\bm{x}))_{x}$    

ですが，一方右辺は，

$\displaystyle \mu_{0}j^{1}(x)=\mu_{0}j_{x}(t,\bm{x})$

です．ですから，

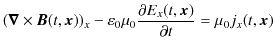
$\displaystyle (\bm{\nabla}\times\bm{B}(t,\bm{x}))_{x}-\varepsilon_{0}\mu_{0}\dfrac{\partial E_{x}(t,\bm{x})}{\partial t}=\mu_{0}j_{x}(t,\bm{x})$

となります．これは，(5.3)式の $ x$ 成分の式です．$ \nu=2,3$ の場合についても，同様な計算により，$ y,z$ 成分の方程式が得られます．

　共変vectorと共変tensorについても同様な式が成立します．

$\displaystyle \fbox{$F_{\mu\nu}(x)\equiv\partial_{\mu}A_{\nu}(x)-\partial_{\nu}A_{\mu}(x)$}$ (5.7)

右辺を計算します．

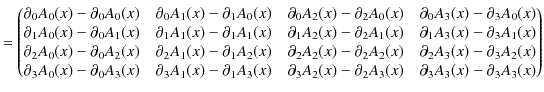$\displaystyle F_{\mu\nu}(x)$ $\displaystyle = \begin{pmatrix} \partial_{0}A_{0}(x)-\partial_{0}A_{0}(x) & \... ...rtial_{2}A_{3}(x) & \partial_{3}A_{3}(x)-\partial_{3}A_{3}(x)\\ \end{pmatrix}$    
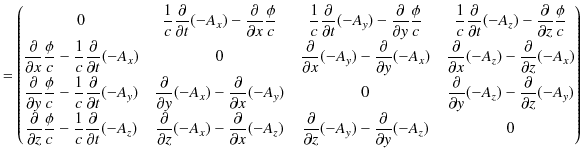  $\displaystyle = \begin{pmatrix} 0 & \dfrac{1}{c}\dfrac{\partial}{\partial t}(... ...al}{\partial z}(-A_{y})-\dfrac{\partial}{\partial y}(-A_{z}) & 0 \end{pmatrix}$    
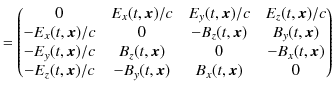  $\displaystyle = \begin{pmatrix} 0 & E_{x}(t,\bm{x})/c & E_{y}(t,\bm{x})/c & E... ...\\ -E_{z}(t,\bm{x})/c & -B_{y}(t,\bm{x}) & B_{x}(t,\bm{x}) & 0 \end{pmatrix}$    

このとき， $ F_{\mu\nu}(x)$ には $ \bm{A}(t,\bm{x})$ と $ \phi(t,\bm{x})$ が含まれていますので，Maxwell方程式(5.2)式と(5.4)式は自動的に成立します．また，Maxwell方程式(5.1)式と(5.3)式は次式で表されます．

$\displaystyle \fbox{$\partial^{\mu}F_{\mu\nu}(x)=\mu_{0}j_{\nu}(x)$}$ (5.8)

この(5.8)式が，確かに(5.1)式と(5.3)式を表していることを確認しておきます．左辺は，

  $\displaystyle \partial^{0}F_{00}(x)+\partial^{1}F_{10}(x)+\partial^{2}F_{20}(x)+\partial^{3}F_{30}(x)$    
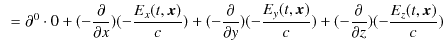  $\displaystyle \,\,\,=\partial^{0}\cdot0+(-\dfrac{\partial}{\partial x})(-\dfrac... ...{y}(t,\bm{x})}{c})+(-\dfrac{\partial}{\partial z})(-\dfrac{E_{z}(t,\bm{x})}{c})$    
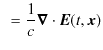  $\displaystyle \,\,\,=\dfrac{1}{c}\bm{\nabla}\cdot\bm{E}(t,\bm{x})$    

ですが，一方右辺は，

$\displaystyle \mu_{0}j_{0}(x)=\mu_{0}(c\rho(t,\bm{x}))$

です．故に，

$\displaystyle \bm{\nabla}\cdot\bm{E}(t,\bm{x})$ $\displaystyle =c^{2}\mu_{0}\rho(t,\bm{x})$    
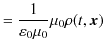  $\displaystyle =\dfrac{1}{\varepsilon_{0}\mu_{0}}\mu_{0}\rho(t,\bm{x})$    
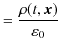  $\displaystyle =\dfrac{\rho(t,\bm{x})}{\varepsilon_{0}}$    

となります．これは，(5.1)式です．また，

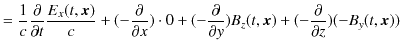$\displaystyle \partial^{0}F_{01}(x)+\partial^{1}F_{11}(x)+\partial^{2}F_{21}(x)+\partial^{3}F_{31}(x)$ $\displaystyle =\dfrac{1}{c}\dfrac{\partial}{\partial t}\dfrac{E_{x}(t,\bm{x})}{... ...}{\partial y})B_{z}(t,\bm{x})+(-\dfrac{\partial}{\partial z})(-B_{y}(t,\bm{x}))$    
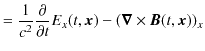  $\displaystyle =\dfrac{1}{c^{2}}\dfrac{\partial}{\partial t}E_{x}(t,\bm{x})-(\bm{\nabla}\times\bm{B}(t,\bm{x}))_{x}$    

ですが，一方右辺は，

$\displaystyle \mu_{0}j_{1}(x)=-\mu_{0}j_{x}(t,\bm{x})$

です．ですから，

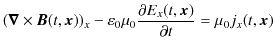
$\displaystyle (\bm{\nabla}\times\bm{B}(t,\bm{x}))_{x}-\varepsilon_{0}\mu_{0}\dfrac{\partial E_{x}(t,\bm{x})}{\partial t}=\mu_{0}j_{x}(t,\bm{x})$

となります．これは，(5.3)式の $ x$ 成分の式です．$ \nu=2,3$ の場合についても，同様な計算により，$ y,z$ 成分の方程式が得られます．

　"Lorentz不変性とLorentz共変性" の Chapter での議論から理解されるように，4元vectorで表されるMaxwell方程式(5.6)式と(5.8)式は，明白なLorentz共変性をもっています．従って，この Chapter の最初に述べたように，Maxwell電磁気学は特殊相対論的です．そして，"特殊相対性原理と光速不変の原理" の Chapter で見たように，Maxwell方程式から光速が導出されるので，光速は座標系に依存しません．故に，光速不変の原理が成立することが保証されたのです．