Chapter4 Lorentz不変性とLorentz共変性

4.1 数学的analogy（3次元Descartes座標における回転座標変換）

このSectionでは数学的な準備のため，特殊相対性理論から少し離れて，3次元空間における簡単な線形代数の復習をしておきます．空間だけの話なので，時間座標は出てきません．あくまで，特殊相対性理論を理解するための，数学的analogyとして取り上げます．

　Descartes座標の $ x$ 軸，$ y$ 軸，$ z$ 軸をとり，任意の3次元座標vector $ (x,y,z)$ をとります．ここで，$ z$ 軸を軸にして $ x$ 軸，$ y$ 軸を反時計回りに $ \theta$ だけ回転させます．そのとき，新しい座標を $ (x',y',z')$ とすると，回転前の古い座標 $ (x,y,z)$ との間に，

  $\displaystyle x'=x\cos\theta+y\sin\theta$    
  $\displaystyle y'=-x\sin\theta+y\cos\theta$    
  $\displaystyle z'=z$    

の関係があります．（図を見て下さい．）

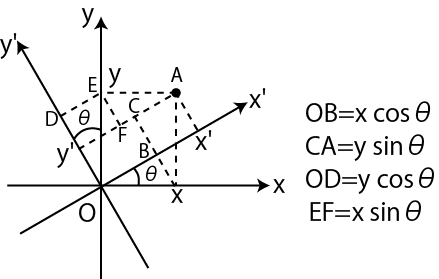
回転座標変換

Figure4.1: 回転座標変換

これらを，行列を使って表すと，

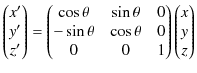
$\displaystyle \begin{pmatrix} x'\\ y'\\ z' \end{pmatrix} =\begin{pmatrix} \... ...eta & 0\\ 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} x\\ y\\ z \end{pmatrix}$

となります．ここで，この関係式を簡略化して表すために表記方法を次のようにします．まず，座標vectorを，

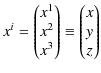
$\displaystyle x^{i}= \begin{pmatrix} x^{1}\\ x^{2}\\ x^{3} \end{pmatrix} \equiv \begin{pmatrix} x\\ y\\ z \end{pmatrix}$

とします．（本 Report "相対性理論" では，アルファベットの $ i,j,k,\ell,m,n$を添え字として使うときは，通常，1,2,3の値をとることにします．）また，回転を表す行列は，

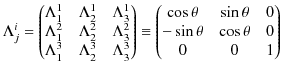
$\displaystyle \Lambda^{i}_{j}= \begin{pmatrix} \Lambda^{1}_{1} & \Lambda^{1}_... ... & \sin\theta & 0\\ -\sin\theta & \cos\theta & 0\\ 0 & 0 & 1 \end{pmatrix}$

とおきます．このとき，上の座標変換の関係式は，

  $\displaystyle x'^{1}=\Lambda^{1}_{1}x^{1}+\Lambda^{1}_{2}x^{2}+\Lambda^{1}_{3}x^{3}$    
  $\displaystyle x'^{2}=\Lambda^{2}_{1}x^{1}+\Lambda^{2}_{2}x^{2}+\Lambda^{2}_{3}x^{3}$    
  $\displaystyle x'^{3}=\Lambda^{3}_{1}x^{1}+\Lambda^{3}_{2}x^{2}+\Lambda^{3}_{3}x^{3}$    

となります．これらの式をまとめて1つの式で表すと，

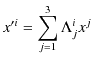
$\displaystyle x'^{i}=\sum_{j=1}^{3}\Lambda^{i}_{j}x^{j}$

となります．なお，$ \Lambda$ 行列は，

$\displaystyle \Lambda^{1}_{1}$ $\displaystyle =\dfrac{\partial x'^{1}}{\partial x^{1}}$ $\displaystyle \Lambda^{1}_{2}$ $\displaystyle =\dfrac{\partial x'^{1}}{\partial x^{2}}$ $\displaystyle \Lambda^{1}_{3}$ $\displaystyle =\dfrac{\partial x'^{1}}{\partial x^{3}}$    
$\displaystyle \Lambda^{2}_{1}$ $\displaystyle =\dfrac{\partial x'^{2}}{\partial x^{1}}$ $\displaystyle \Lambda^{2}_{2}$ $\displaystyle =\dfrac{\partial x'^{2}}{\partial x^{2}}$ $\displaystyle \Lambda^{2}_{3}$ $\displaystyle =\dfrac{\partial x'^{2}}{\partial x^{3}}$    
$\displaystyle \Lambda^{3}_{1}$ $\displaystyle =\dfrac{\partial x'^{3}}{\partial x^{1}}$ $\displaystyle \Lambda^{3}_{2}$ $\displaystyle =\dfrac{\partial x'^{3}}{\partial x^{2}}$ $\displaystyle \Lambda^{3}_{3}$ $\displaystyle =\dfrac{\partial x'^{3}}{\partial x^{3}}$    

の関係がありますので，

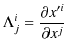
$\displaystyle \Lambda^{i}_{j}=\dfrac{\partial x'^{i}}{\partial x^{j}}$

と表すことができます．再度，回転座標変換の式を書くと，

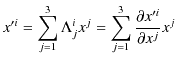
$\displaystyle x'^{i}=\sum_{j=1}^{3}\Lambda^{i}_{j}x^{j}=\sum_{j=1}^{3}\dfrac{\partial x'^{i}}{\partial x^{j}}x^{j}$

とまとめられます．

　それでは，回転の逆変換はどのようになるのでしょうか．変換の行列は，$ \theta$ を $ -\theta$ に置き換えて，

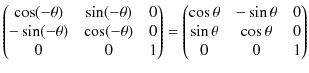
$\displaystyle \begin{pmatrix} \cos(-\theta) & \sin(-\theta) & 0\\ -\sin(-\th... ...in\theta & 0\\ \sin⁡\theta & \cos⁡\theta & 0\\ 0 & 0 & 1 \end{pmatrix}$

となります．したがって，逆変換の関係式は，

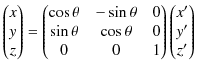
$\displaystyle \begin{pmatrix} x\\ y\\ z \end{pmatrix} = \begin{pmatrix} \c... ... & 0\\ 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} x'\\ y'\\ z' \end{pmatrix}$

です．この逆変換の行列を，

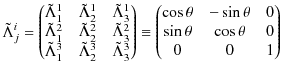
$\displaystyle \tilde{\Lambda}^{i}_{j}= \begin{pmatrix} \tilde{\Lambda}^{1}_{1... ... -\sin\theta & 0\\ \sin\theta & \cos\theta & 0\\ 0 & 0 & 1 \end{pmatrix} $

とおきます．このとき，

  $\displaystyle x^{1}=\tilde{\Lambda}^{1}_{1}x'^{1}+\tilde{\Lambda}^{1}_{2}x'^{2}+\tilde{\Lambda}^{1}_{3}x'^{3}$    
  $\displaystyle x^{2}=\tilde{\Lambda}^{2}_{1}x'^{1}+\tilde{\Lambda}^{2}_{2}x'^{2}+\tilde{\Lambda}^{2}_{3}x'^{3}$    
  $\displaystyle x^{3}=\tilde{\Lambda}^{3}_{1}x'^{1}+\tilde{\Lambda}^{3}_{2}x'^{2}+\tilde{\Lambda}^{3}_{3}x'^{3}$    

となります．これらの式をまとめて1つの式で表すと，

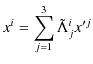
$\displaystyle x^{i}=\sum_{j=1}^{3}\tilde{\Lambda}^{i}_{j}x'^{j}$

となります．なお， $ \tilde{\Lambda}$ 行列は，

$\displaystyle \tilde{\Lambda}^{1}_{1}$ $\displaystyle =\dfrac{\partial x^{1}}{\partial x'^{1}}$ $\displaystyle \tilde{\Lambda}^{1}_{2}$ $\displaystyle =\dfrac{\partial x^{1}}{\partial x'^{2}}$ $\displaystyle \tilde{\Lambda}^{1}_{3}$ $\displaystyle =\dfrac{\partial x^{1}}{\partial x'^{3}}$    
$\displaystyle \tilde{\Lambda}^{2}_{1}$ $\displaystyle =\dfrac{\partial x^{2}}{\partial x'^{1}}$ $\displaystyle \tilde{\Lambda}^{2}_{2}$ $\displaystyle =\dfrac{\partial x^{2}}{\partial x'^{2}}$ $\displaystyle \tilde{\Lambda}^{2}_{3}$ $\displaystyle =\dfrac{\partial x^{2}}{\partial x'^{3}}$    
$\displaystyle \tilde{\Lambda}^{3}_{1}$ $\displaystyle =\dfrac{\partial x^{3}}{\partial x'^{1}}$ $\displaystyle \tilde{\Lambda}^{3}_{2}$ $\displaystyle =\dfrac{\partial x^{3}}{\partial x'^{2}}$ $\displaystyle \tilde{\Lambda}^{3}_{3}$ $\displaystyle =\dfrac{\partial x^{3}}{\partial x'^{3}}$    

の関係がありますので，

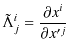
$\displaystyle \tilde{\Lambda}^{i}_{j}=\dfrac{\partial x^{i}}{\partial x'^{j}}$

と表すことができます．再度，回転座標逆変換の式を書くと，

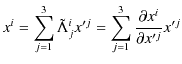
$\displaystyle x^{i}=\sum_{j=1}^{3}\tilde{\Lambda}^{i}_{j}x'^{j}=\sum_{j=1}^{3}\dfrac{\partial x^{i}}{\partial x'^{j}}x'^{j}$

とまとめられます．

$ \Lambda$ 行列と $ \tilde{\Lambda}$ 行列は逆行列の関係にあります．このことは，直接，行列を掛け合わせれば確認できます．

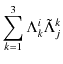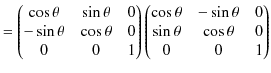$\displaystyle \sum_{k=1}^{3}\Lambda^{i}_{k}\tilde{\Lambda}^{k}_{j}$ $\displaystyle = \begin{pmatrix} \cos\theta & \sin\theta & 0\\ -\sin\theta &... ... & -\sin\theta & 0\\ \sin\theta & \cos\theta & 0\\ 0 & 0 & 1 \end{pmatrix}$    
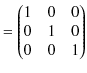  $\displaystyle = \begin{pmatrix} 1 & 0 & 0\\ 0 & 1 & 0\\ 0 & 0 & 1 \end{pmatrix}$    

あるいは，偏微分の性質を使っても導出できます．

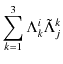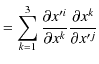$\displaystyle \sum_{k=1}^{3}\Lambda^{i}_{k}\tilde{\Lambda}^{k}_{j}$ $\displaystyle =\sum_{k=1}^{3}\dfrac{\partial x'^{i}}{\partial x^{k}}\dfrac{\partial x^{k}}{\partial x'^{j}}$    
  $\displaystyle =\dfrac{\partial x'^{i}}{\partial x'^{j}}$    
  $\displaystyle =\delta^{i}_{j}$    

ただし，最後の記号はKroneckerのデルタで，

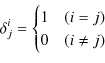
\begin{displaymath}\delta^{i}_{j}= \begin{cases}1 & (i=j)\\ 0 & (i\neq j) \end{cases}\end{displaymath}

を意味します．

 

4.2 Lorentz変換の4次元定式化

前のSectionと並行して，4次元の座標変換であるLorentz変換について数学的に再考してみましょう．Lorentz変換を再掲すると，

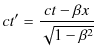  $\displaystyle ct'=\dfrac{ct-\beta x}{\sqrt{1-\beta^{2}}}$    
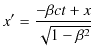  $\displaystyle x'=\dfrac{-\beta ct+x}{\sqrt{1-\beta^{2}}}$    
  $\displaystyle y'=y$    
  $\displaystyle z'=z$    

であり，Lorentz逆変換は，

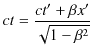  $\displaystyle ct=\dfrac{ct'+\beta x'}{\sqrt{1-\beta^{2}}}$    
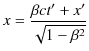  $\displaystyle x=\dfrac{\beta ct'+x'}{\sqrt{1-\beta^{2}}}$    
  $\displaystyle y=y'$    
  $\displaystyle z=z'$    

でした．ここで，Lorentz変換を，行列を使って表すと，

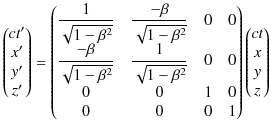
$\displaystyle \begin{pmatrix} ct'\\ x'\\ y'\\ z' \end{pmatrix} = \begin{pma... ... 0 & 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} ct\\ x\\ y\\ z \end{pmatrix}$

となります．また，Lorentz逆変換も，同様に次のように表せます．

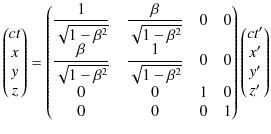
$\displaystyle \begin{pmatrix} ct\\ x\\ y\\ z \end{pmatrix} = \begin{pmatrix... ... & 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} ct'\\ x'\\ y'\\ z' \end{pmatrix}$

　これらの行列の関係式をシンプルに表す方法を考えましょう．まず，座標vectorですが，

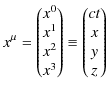
$\displaystyle x^{\mu}= \begin{pmatrix} x^{0}\\ x^{1}\\ x^{2}\\ x^{3} \end{pmatrix} \equiv \begin{pmatrix} ct\\ x\\ y\\ z \end{pmatrix}$

と表します．上付きの添え字 $ \mu$ は0,1,2,3の値をとるのですね．（相対性理論では，特に断りがない限り，ギリシア文字は0,1,2,3の値をとります．）このような時間1成分と空間3成分からなるvectorを4元vectorといいます．そして，Lorentz変換の行列ですが，

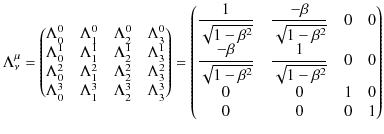
$\displaystyle \Lambda^{\mu}_{\nu}= \begin{pmatrix} \Lambda^{0}_{0} & \Lambda^... ...{\sqrt{1-\beta^{2}}} & 0 & 0\\ 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 1 \end{pmatrix}$

とおくことにします．$ \mu$ は行を，$ \nu$ は列を表していて，それぞれ，0,1,2,3の値をとります．このとき，Lorentz変換は，

  $\displaystyle x'^{0}=\Lambda^{0}_{0}x^{0}+\Lambda^{0}_{1}x^{1}+\Lambda^{0}_{2}x^{2}+\Lambda^{0}_{3}x^{3}$    
  $\displaystyle x'^{1}=\Lambda^{1}_{0}x^{0}+\Lambda^{1}_{1}x^{1}+\Lambda^{1}_{2}x^{2}+\Lambda^{1}_{3}x^{3}$    
  $\displaystyle x'^{2}=\Lambda^{2}_{0}x^{0}+\Lambda^{2}_{1}x^{1}+\Lambda^{2}_{2}x^{2}+\Lambda^{2}_{3}x^{3}$    
  $\displaystyle x'^{3}=\Lambda^{3}_{0}x^{0}+\Lambda^{3}_{1}x^{1}+\Lambda^{3}_{2}x^{2}+\Lambda^{3}_{3}x^{3}$    

となりますが，1つにまとめて，

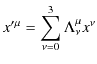
$\displaystyle x'^{\mu}=\sum_{\nu=0}^{3}\Lambda^{\mu}_{\nu}x^{\nu}$

となります．ここで，記号の約束ですが，同じギリシア文字の添え字が上下に対になって現れたときには，和の記号を省略できるとします．そして，和の記号なしで，その同じ添え字について0,1,2,3の和をとります．この約束をEinsteinの規約といいます．ですから，この式は，

$\displaystyle x'^{\mu}=\Lambda^{\mu}_{\nu}x^{\nu}$

と書くことができます．（かなり簡略化してLorentz変換を表せました．）したがって，$ \Lambda$ 行列は次のように表せます．

$\displaystyle \Lambda^{0}_{0}$ $\displaystyle =\dfrac{\partial x'^{0}}{\partial x^{0}}$ $\displaystyle \Lambda^{0}_{1}$ $\displaystyle =\dfrac{\partial x'^{0}}{\partial x^{1}}$ $\displaystyle \Lambda^{0}_{2}$ $\displaystyle =\dfrac{\partial x'^{0}}{\partial x^{2}}$ $\displaystyle \Lambda^{0}_{3}$ $\displaystyle =\dfrac{\partial x'^{0}}{\partial x^{3}}$    
$\displaystyle \Lambda^{1}_{0}$ $\displaystyle =\dfrac{\partial x'^{1}}{\partial x^{0}}$ $\displaystyle \Lambda^{1}_{1}$ $\displaystyle =\dfrac{\partial x'^{1}}{\partial x^{1}}$ $\displaystyle \Lambda^{1}_{2}$ $\displaystyle =\dfrac{\partial x'^{1}}{\partial x^{2}}$ $\displaystyle \Lambda^{1}_{3}$ $\displaystyle =\dfrac{\partial x'^{1}}{\partial x^{3}}$    
$\displaystyle \Lambda^{2}_{0}$ $\displaystyle =\dfrac{\partial x'^{2}}{\partial x^{0}}$ $\displaystyle \Lambda^{2}_{1}$ $\displaystyle =\dfrac{\partial x'^{2}}{\partial x^{1}}$ $\displaystyle \Lambda^{2}_{2}$ $\displaystyle =\dfrac{\partial x'^{2}}{\partial x^{2}}$ $\displaystyle \Lambda^{2}_{3}$ $\displaystyle =\dfrac{\partial x'^{2}}{\partial x^{3}}$    
$\displaystyle \Lambda^{3}_{0}$ $\displaystyle =\dfrac{\partial x'^{3}}{\partial x^{0}}$ $\displaystyle \Lambda^{3}_{1}$ $\displaystyle =\dfrac{\partial x'^{3}}{\partial x^{1}}$ $\displaystyle \Lambda^{3}_{2}$ $\displaystyle =\dfrac{\partial x'^{3}}{\partial x^{2}}$ $\displaystyle \Lambda^{3}_{3}$ $\displaystyle =\dfrac{\partial x'^{3}}{\partial x^{3}}$    

1式にまとめると，

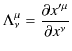
$\displaystyle \Lambda^{\mu}_{\nu}=\dfrac{\partial x'^{\mu}}{\partial x^{\nu}}$

となります．ここで，Lorentz変換をまとめて，

$\displaystyle x'^{\mu}=\Lambda^{\mu}_{\nu}x^{\nu}=\dfrac{\partial x'^{\mu}}{\partial x^{\nu}}x^{\nu}$ (4.1)

としておきます．

　それでは，Lorentz逆変換も同じように簡略化して表しておきます．逆変換の行列を，

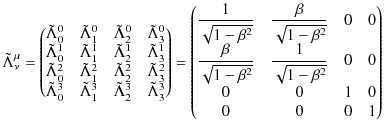
$\displaystyle \tilde{\Lambda}^{\mu}_{\nu}= \begin{pmatrix} \tilde{\Lambda}^{0... ...{\sqrt{1-\beta^{2}}} & 0 & 0\\ 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 1 \end{pmatrix}$

とおきます．このとき，Lorentz逆変換は，

  $\displaystyle x^{0}=\tilde{\Lambda}^{0}_{0}x'^{0}+\tilde{\Lambda}^{0}_{1}x'^{1}+\tilde{\Lambda}^{0}_{2}x'^{2}+\tilde{\Lambda}^{0}_{3}x'^{3}$    
  $\displaystyle x^{1}=\tilde{\Lambda}^{1}_{0}x'^{0}+\tilde{\Lambda}^{1}_{1}x'^{1}+\tilde{\Lambda}^{1}_{2}x'^{2}+\tilde{\Lambda}^{1}_{3}x'^{3}$    
  $\displaystyle x^{2}=\tilde{\Lambda}^{2}_{0}x'^{0}+\tilde{\Lambda}^{2}_{1}x'^{1}+\tilde{\Lambda}^{2}_{2}x'^{2}+\tilde{\Lambda}^{2}_{3}x'^{3}$    
  $\displaystyle x^{3}=\tilde{\Lambda}^{3}_{0}x'^{0}+\tilde{\Lambda}^{3}_{1}x'^{1}+\tilde{\Lambda}^{3}_{2}x'^{2}+\tilde{\Lambda}^{3}_{3}x'^{3}$    

となりますので，

$\displaystyle x^{\mu}=\tilde{\Lambda}^{\mu}_{\nu}x'^{\nu}$

と表せます．（ここでも，Einsteinの規約を使いました．）したがって， $ \tilde{\Lambda}$ 行列は次のようになります．

$\displaystyle \tilde{\Lambda}^{0}_{0}$ $\displaystyle =\dfrac{\partial x^{0}}{\partial x'^{0}}$ $\displaystyle \tilde{\Lambda}^{0}_{1}$ $\displaystyle =\dfrac{\partial x^{0}}{\partial x'^{1}}$ $\displaystyle \tilde{\Lambda}^{0}_{2}$ $\displaystyle =\dfrac{\partial x^{0}}{\partial x'^{2}}$ $\displaystyle \tilde{\Lambda}^{0}_{3}$ $\displaystyle =\dfrac{\partial x^{0}}{\partial x'^{3}}$    
$\displaystyle \tilde{\Lambda}^{1}_{0}$ $\displaystyle =\dfrac{\partial x^{1}}{\partial x'^{0}}$ $\displaystyle \tilde{\Lambda}^{1}_{1}$ $\displaystyle =\dfrac{\partial x^{1}}{\partial x'^{1}}$ $\displaystyle \tilde{\Lambda}^{1}_{2}$ $\displaystyle =\dfrac{\partial x^{1}}{\partial x'^{2}}$ $\displaystyle \tilde{\Lambda}^{1}_{3}$ $\displaystyle =\dfrac{\partial x^{1}}{\partial x'^{3}}$    
$\displaystyle \tilde{\Lambda}^{2}_{0}$ $\displaystyle =\dfrac{\partial x^{2}}{\partial x'^{0}}$ $\displaystyle \tilde{\Lambda}^{2}_{1}$ $\displaystyle =\dfrac{\partial x^{2}}{\partial x'^{1}}$ $\displaystyle \tilde{\Lambda}^{2}_{2}$ $\displaystyle =\dfrac{\partial x^{2}}{\partial x'^{2}}$ $\displaystyle \tilde{\Lambda}^{2}_{3}$ $\displaystyle =\dfrac{\partial x^{2}}{\partial x'^{3}}$    
$\displaystyle \tilde{\Lambda}^{3}_{0}$ $\displaystyle =\dfrac{\partial x^{3}}{\partial x'^{0}}$ $\displaystyle \tilde{\Lambda}^{3}_{1}$ $\displaystyle =\dfrac{\partial x^{3}}{\partial x'^{1}}$ $\displaystyle \tilde{\Lambda}^{3}_{2}$ $\displaystyle =\dfrac{\partial x^{3}}{\partial x'^{2}}$ $\displaystyle \tilde{\Lambda}^{3}_{3}$ $\displaystyle =\dfrac{\partial x^{3}}{\partial x'^{3}}$    

の関係がありますので，

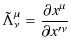
$\displaystyle \tilde{\Lambda}^{\mu}_{\nu}=\dfrac{\partial x^{\mu}}{\partial x'^{\nu}}$

となります．Lorentz逆変換をまとめて，

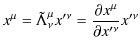
$\displaystyle x^{\mu}=\tilde{\Lambda}^{\mu}_{\nu}x'^{\nu}=\dfrac{\partial x^{\mu}}{\partial x'^{\nu}}x'^{\nu}$

としておきます．

　$ \Lambda$ 行列と $ \tilde{\Lambda}$ 行列はお互いに逆行列の関係にあることがわかります．直接，行列を掛け合わせてみて，

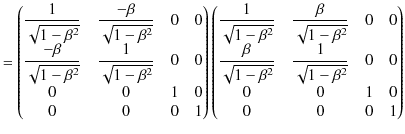$\displaystyle \Lambda^{\mu}_{\rho}\tilde{\Lambda}^{\rho}_{\nu}$ $\displaystyle = \begin{pmatrix} \dfrac{1}{\sqrt{1-\beta^{2}}} & \dfrac{-\beta... ...{\sqrt{1-\beta^{2}}} & 0 & 0\\ 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 1 \end{pmatrix}$    
  $\displaystyle = \begin{pmatrix} 1 & 0 & 0 & 0\\ 0 & 1 & 0 & 0\\ 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 1 \end{pmatrix}$    

と確認することができます．あるいは，偏微分の性質を使っても，証明できます．

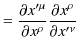$\displaystyle \Lambda^{\mu}_{\rho}\tilde{\Lambda}^{\rho}_{\nu}$ $\displaystyle =\dfrac{\partial x'^{\mu}}{\partial x^{\rho}}\dfrac{\partial x^{\rho}}{\partial x'^{\nu}}$    
  $\displaystyle =\dfrac{\partial x'^{\mu}}{\partial x'^{\nu}}$    
  $\displaystyle =\delta^{\mu}_{\nu}$    

ただし， $ \delta^{\mu}_{\nu}$ はKroneckerのデルタで，

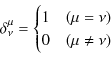
\begin{displaymath}\delta^{\mu}_{\nu}= \begin{cases} 1 & (\mu=\nu)\\ 0 & (\mu\neq\nu) \end{cases}\end{displaymath}

と定義されます．

 

4.3 IntervalのLorentz不変性

Interval $ s$ の2乗は，

$\displaystyle s^{2}\equiv(ct)^{2}-x^{2}-y^{2}-z^{2}$

で定義されました．ここで，座標vectorについて，反変vectorと共変vectorというものを導入します．反変vectorの座標vectorは添え字が上付きと約束し，今まで取り扱ってきた座標vectorを意味します．

$\displaystyle x^{\mu}$ $\displaystyle =(x^{0},x^{1},x^{2},x^{3})$    
  $\displaystyle \equiv(ct,x,y,z)$    
  $\displaystyle =(ct,\bm{x})$    

共変vectorの座標vectorは添え字が下付きと約束し，今まで取り扱ってきた座標vectorの空間成分のみを逆符号とします．

$\displaystyle x_{\mu}$ $\displaystyle =(x_{0},x_{1},x_{2},x_{3})$    
  $\displaystyle \equiv(x^{0},-x^{1},-x^{2},-x^{3})$    
  $\displaystyle =(ct,-x,-y,-z)$    
  $\displaystyle =(ct,-\bm{x})$    

このとき，intervalの2乗は，

$\displaystyle s^{2}$ $\displaystyle =x^{\mu}x_{\mu}$    
  $\displaystyle =x^{0}x_{0}+x^{1}x_{1}+x^{2}x_{2}+x^{3}x_{3}$    
  $\displaystyle =(ct)^{2}-x^{2}-y^{2}-z^{2}$    

と表すことができます． $ x^{\mu}x_{\mu}$ のように，vector2つの積で添え字が2個あっても上下対になっていて和をとる場合は，縮約といってvectorの積はscalarになります．そして，一般にscalarはLorentz変換に対して不変量になります．今考えているintervalの2乗の量がLorentz不変量になることは，"Lorentz変換とMinkowski時空" のChapterで，直接確認しましたね．

　このように，反変vectorと共変vectorは添え字の上下が異なり，空間成分の符号が違います．そこで，この2つのvectorを変換するために計量tensorと呼ばれる次のtensorを導入します．

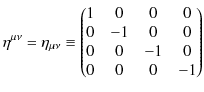
$\displaystyle \eta^{\mu\nu}=\eta_{\mu\nu}\equiv \begin{pmatrix} 1 & 0 & 0 & 0\\ 0 & -1 & 0 & 0\\ 0 & 0 & -1 & 0\\ 0 & 0 & 0 & -1 \end{pmatrix}$

この計量tensorを使うと，反変vectorと共変vectorの間を変換することができます．

$\displaystyle \eta_{\mu\nu}x^{\nu}$ $\displaystyle =\eta_{\mu0}x^{0}+\eta_{\mu1}x^{1}+\eta_{\mu2}x^{2}+\eta_{\mu3}x^{3}$    
  $\displaystyle =(x^{0},0,0,0)+(0,-x^{1},0,0)+(0,0,-x^{2},0)+(0,0,0,-x^{3})$    
  $\displaystyle =(x^{0},-x^{1},-x^{2},-x^{3})$    
  $\displaystyle =x_{\mu}$    

あるいは，

$\displaystyle \eta^{\mu\nu}x_{\nu}$ $\displaystyle =\eta^{\mu0}x_{0}+\eta^{\mu1}x_{1}+\eta^{\mu2}x_{2}+\eta^{\mu3}x_{3}$    
  $\displaystyle =(x_{0},0,0,0)+(0,-x_{1},0,0)+(0,0,-x_{2},0)+(0,0,0,-x_{3})$    
  $\displaystyle =(x_{0},-x_{1},-x_{2},-x_{3})$    
  $\displaystyle =(x^{0},x^{1},x^{2},x^{3})$    
  $\displaystyle =x^{\mu}$    

です．このとき，intervalの2乗は，

$\displaystyle s^{2}$ $\displaystyle =\eta^{\mu\nu}x_{\mu}x_{\nu}=x^{\nu}x_{\nu}$    
  $\displaystyle =\eta_{\mu\nu}x^{\mu}x^{\nu}=x_{\nu}x^{\nu}$    

と表すことができます．そして，intervalの2乗の変換後のダッシュの付いた量は，

$\displaystyle s'^{2}$ $\displaystyle =\eta_{\mu\nu}x'^{\mu}x'^{\nu}$    
  $\displaystyle =\eta_{\mu\nu}\Lambda^{\mu}_{\rho}\Lambda^{\nu}_{\sigma}x^{\rho}x^{\sigma}$    

となります．ここで，$ \mu$ を $ \rho$ に，$ \nu$ を $ \sigma$ に，$ \rho$ を $ \mu$ に，$ \sigma$ を $ \nu$ にそっくりと入れ替えても問題ありません．（Einsteinの規約で，上下対になって縮約されている添え字は他のギリシア文字とそっくり入れ替えても，結局0,1,2,3と和をとるだけなので同じことになります．）

$\displaystyle s'^{2}$ $\displaystyle =\eta_{\mu\nu}\Lambda^{\mu}_{\rho}\Lambda^{\nu}_{\sigma}x^{\rho}x^{\sigma}$    
  $\displaystyle =\eta_{\rho\sigma}\Lambda^{\rho}_{\mu}\Lambda^{\sigma}_{\nu}x^{\mu}x^{\nu}$    

Intervalの2乗のLorentz不変性より，最後の式の量は，

$\displaystyle s^{2}=\eta_{\mu\nu}x^{\mu}x^{\nu}$

に等しくなります．したがって，

$\displaystyle \eta_{\rho\sigma}\Lambda^{\rho}_{\mu}\Lambda^{\sigma}_{\nu}=\eta_{\mu\nu}$ (4.2)

という等式が成立します．一般に，(4.2)式を満たす行列 $ \Lambda$ で変換する座標変換はintervalを不変に保つことができます．この座標変換を一般Lorentz変換と言います．一般Lorentz変換では座標が等速直線運動する方向は任意に選べます．それに対して，今までの $ x$ 方向に等速直線運動している特別な場合のLorentz変換を特殊Lorentz変換と言います．

　$ x^{\mu}$ は，

$\displaystyle x^{\mu}$ $\displaystyle =(x^{0},x^{1},x^{2},x^{3})$    
  $\displaystyle \equiv(ct,x,y,z)$    
  $\displaystyle =(ct,\bm{x})$    

と表され，変換式(4.1)式，

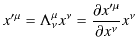
$\displaystyle x'^{\mu}=\Lambda^{\mu}_{\nu}x^{\nu}=\dfrac{\partial x'^{\mu}}{\partial x^{\nu}}x^{\nu}$

が成立しました．一方，$ x_{\mu}$ は，

$\displaystyle x_{\mu}$ $\displaystyle =(x_{0},x_{1},x_{2},x_{3})$    
  $\displaystyle \equiv(x^{0},-x^{1},-x^{2},-x^{3})=\eta_{\mu\nu}x^{\nu}$    
  $\displaystyle =(ct,-x,-y,-z)$    
  $\displaystyle =(ct,-\bm{x})$    

と表されましたが，座標変換はどのようになるのでしょうか？ まず，次の計算を確認します．

$\displaystyle x'_{\mu}$ $\displaystyle =\eta_{\mu\nu}x'^{\nu}$    
  $\displaystyle =\eta_{\mu\nu}\Lambda^{\nu}_{\rho}x^{\rho}$    

ですから，

$\displaystyle x'_{\mu}=\eta_{\mu\nu}\Lambda^{\nu}_{\rho}\eta^{\rho\sigma}x_{\sigma}$ (4.3)

です．ここで， $ \eta_{\mu\nu}\Lambda^{\nu}_{\rho}\eta^{\rho\sigma}$ が $ \Lambda$ の逆行列 $ \tilde{\Lambda}$ と同定できることは，次のように確認できます．この量に $ \Lambda^{\mu}_{\kappa}$ をかけて $ \mu$ について縮約をとった量を $ P$ とおくと，

$\displaystyle P^{\sigma}_{\kappa}$ $\displaystyle =\eta_{\mu\nu}\Lambda^{\nu}_{\rho}\eta^{\rho\sigma}\cdot\Lambda^{\mu}_{\kappa}$    
  $\displaystyle =\eta_{\mu\nu}\Lambda^{\mu}_{\kappa}\Lambda^{\nu}_{\rho}\cdot\eta^{\rho\sigma}$    

となります．少し上の(4.2)式，

$\displaystyle \eta_{\rho\sigma}\Lambda^{\rho}_{\mu}\Lambda^{\sigma}_{\nu}=\eta_{\mu\nu}$

より，

$\displaystyle P^{\sigma}_{\kappa}$ $\displaystyle =\eta_{\kappa\rho}\cdot\eta^{\rho\sigma}$    
  $\displaystyle =\delta^{\sigma}_{\kappa}$    

です．よって， $ \eta_{\mu\nu}\Lambda^{\nu}_{\rho}\eta^{\rho\sigma}$は $ \Lambda$ の逆行列 $ \tilde{\Lambda}^{\sigma}_{\mu}$ となります．故に，(4.3)式より，

$\displaystyle x'_{\mu}=\tilde{\Lambda}^{\sigma}_{\mu}x_{\sigma}$

となります．縮約をとっている $ \sigma$ を $ \nu$ に置き換えて，共変vectorの変換性は，

$\displaystyle x'_{\mu}=\tilde{\Lambda}^{\nu}_{\mu}x_{\nu}$

となります．さらに，

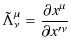
$\displaystyle \tilde{\Lambda}^{\mu}_{\nu}=\dfrac{\partial x^{\mu}}{\partial x'^{\nu}}$

の関係がありましたので，

$\displaystyle x'_{\mu}=\tilde{\Lambda}^{\nu}_{\mu}x_{\nu}=\dfrac{\partial x^{\nu}}{\partial x'^{\mu}}x_{\nu}$ (4.4)

とまとめられます．この(4.4)式は，$ x_{\mu}$ のLorentz変換です．

 

4.4 Scalar，vector，tensor

今までのSectionでは，座標vectorと座標変換であるLorentz変換について議論してきましたが，物理量を表す4元vectorといわれる量を一般的に導入しましょう．（座標vectorも4元vectorに含まれます．）まず，一般的に反変vectorを，

$\displaystyle A^{\mu}$ $\displaystyle \equiv(A^{0},A^{1},A^{2},A^{3})$    
  $\displaystyle \equiv(A^{0},A_{x},A_{y},A_{z})$    
  $\displaystyle =(A^{0},\bm{A})$    

とします．そして，$ x^{\mu}$ のLorentz変換(4.1)式，

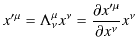
$\displaystyle x'^{\mu}=\Lambda^{\mu}_{\nu}x^{\nu}=\dfrac{\partial x'^{\mu}}{\partial x^{\nu}}x^{\nu}$

と同様に，

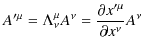$\displaystyle A'^{\mu}=\Lambda^{\mu}_{\nu}A^{\nu}=\dfrac{\partial x'^{\mu}}{\partial x^{\nu}}A^{\nu}$ (4.5)

と変換するとし，この変換によって反変vectorを定義します．次に共変vectorを，

$\displaystyle A_{\mu}$ $\displaystyle \equiv(A_{0},A_{1},A_{2},A_{3})$    
  $\displaystyle =(A^{0},-A^{1},-A^{2},-A^{3})=\eta_{\mu\nu}A^{\nu}$    
  $\displaystyle =(A^{0},-A_{x},-A_{y},-A_{z})$    
  $\displaystyle =(A^{0},-\bm{A})$    

とします．そして，共変vectorの座標vectorのLorentz変換(4.4)式，

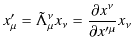
$\displaystyle x'_{\mu}=\tilde{\Lambda}^{\nu}_{\mu}x_{\nu}=\dfrac{\partial x^{\nu}}{\partial x'^{\mu}}x_{\nu}$

と同様に，

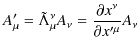$\displaystyle A'_{\mu}=\tilde{\Lambda}^{\nu}_{\mu}A_{\nu}=\dfrac{\partial x^{\nu}}{\partial x'^{\mu}}A_{\nu}$ (4.6)

と変換するとし，この変換によって共変vectorを定義します．

　反変vector1個と共変vector1個を掛け合わせ，同じ添え字にして縮約をとった量をscalarといいます．例えば，

$\displaystyle A^{\mu}A_{\mu},\,P_{\nu}P^{\nu},\,\eta_{\mu\nu}A^{\mu}B^{\nu}$

等です．Scalarは全ての添え字が縮約をとられているので，実質添え字が0個で，Lorentz不変量になります．反変vectorの座標vectorと共変vectorの座標vectorからできているintervalもscalarの具体例です．

　反変vectorを2つ掛け合わせてできた量を2階反変tensorといいます．式で表すと，

$\displaystyle T^{\mu\nu}=A^{\mu}B^{\nu}$

のようになります．このtensorの変換は，

$\displaystyle T'^{\mu\nu}$ $\displaystyle =A'^{\mu}B'^{\nu}$    
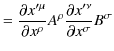  $\displaystyle =\dfrac{\partial x'^{\mu}}{\partial x^{\rho}}A^{\rho}\dfrac{\partial x'^{\nu}}{\partial x^{\sigma}}B^{\sigma}$    
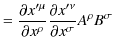  $\displaystyle =\dfrac{\partial x'^{\mu}}{\partial x^{\rho}}\dfrac{\partial x'^{\nu}}{\partial x^{\sigma}}A^{\rho}B^{\sigma}$    

ですから，

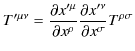
$\displaystyle T'^{\mu\nu}=\dfrac{\partial x'^{\mu}}{\partial x^{\rho}}\dfrac{\partial x'^{\nu}}{\partial x^{\sigma}}T^{\rho\sigma}$

のようになります．一方，共変vectorを2つ掛け合わせてできた量を2階共変tensorといいます．式で表すと，

$\displaystyle T_{\mu\nu}=A_{\mu}B_{\nu}$

のようになります．このtensorの変換は，

$\displaystyle T'_{\mu\nu}$ $\displaystyle =A'_{\mu}B'_{\nu}$    
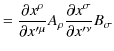  $\displaystyle =\dfrac{\partial x^{\rho}}{\partial x'^{\mu}}A_{\rho}\dfrac{\partial x^{\sigma}}{\partial x'^{\nu}}B_{\sigma}$    
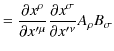  $\displaystyle =\dfrac{\partial x^{\rho}}{\partial x'^{\mu}}\dfrac{\partial x^{\sigma}}{\partial x'^{\nu}}A_{\rho}B_{\sigma}$    

ですから，

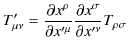
$\displaystyle T'_{\mu\nu}=\dfrac{\partial x^{\rho}}{\partial x'^{\mu}}\dfrac{\partial x^{\sigma}}{\partial x'^{\nu}}T_{\rho\sigma}$

のようになります．ここでは，反変および共変vectorから，それぞれ反変および共変tensorをつくりましたが，上の2つの変換式によって，tensorを定義することができます．

　反変成分が上付き，共変成分が下付きなのですが，計量tensorによって上付きと下付きを入れ替えることができます．いくつか例をあげておきます．

  $\displaystyle \eta^{\mu\nu}A_{\nu}=A^{\mu}$    
  $\displaystyle \eta_{\mu\rho}T^{\rho\nu}=T^{\nu}_{\mu}$    
  $\displaystyle \eta^{\mu\rho}\eta^{\nu\sigma}T_{\rho\sigma}=T^{\mu\nu}$    

2番目の例のように，上付きの添え字と下付きの添え字が混ざっているtensorを混合tensorと言います．

　特殊相対性理論の物理量は場で表されます．場とは，その量が空間に依存し，時間的に変動するものでした．つまり，

$\displaystyle x$ $\displaystyle \equiv x^{\mu}$    
  $\displaystyle =(x^{0},x^{1},x^{2},x^{3})$    
  $\displaystyle =(ct,x,y,z)$    
  $\displaystyle =(ct,\bm{x})$    

の関数で表される量です．Scalar場は，

$\displaystyle C(x)$

のように表記され，

$\displaystyle C(x)=C'(x')$

の関係を満たします．（ここで，$ x$ と $ x'$ は，同じ世界点の $ M(ct,x,y,z)$， $ M'(ct',x',y',z')$ からみた座標です．）反変vector場と共変vector場は，

  $\displaystyle A^{\mu}(x)$    
  $\displaystyle A_{\mu}(x)$    

のように表記され，

  $\displaystyle A'^{\mu}(x')=\dfrac{\partial x'^{\mu}}{\partial x^{\nu}}A^{\nu}(x)$    
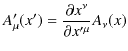  $\displaystyle A'_{\mu}(x')=\dfrac{\partial x^{\nu}}{\partial x'^{\mu}}A_{\nu}(x)$    

の変換則を満たします．同様に，反変tensor場と共変tensor場は，

  $\displaystyle A^{\mu\nu}(x)$    
  $\displaystyle A_{\mu\nu}(x)$    

のように表記され，

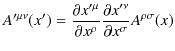  $\displaystyle A'^{\mu\nu}(x')=\dfrac{\partial x'^{\mu}}{\partial x^{\rho}}\dfrac{\partial x'^{\nu}}{\partial x^{\sigma}}A^{\rho\sigma}(x)$    
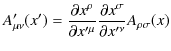  $\displaystyle A'_{\mu\nu}(x')=\dfrac{\partial x^{\rho}}{\partial x'^{\mu}}\dfrac{\partial x^{\sigma}}{\partial x'^{\nu}}A_{\rho\sigma}(x)$    

の変換則を満たします．

 

4.5 Lorentz共変性

ここで，特殊相対性原理，

　"物理法則は全ての慣性系において，同じ形式で表現されます．"

の要請を満たす物理学を構築することを考えましょう．一般に，物理法則は幾つかの物理量を結ぶ方程式の関係で表現されます．物理法則を表現する方程式がLorentz変換のもとで同じ形式で表されれば要請は満足されていることになります．方程式がLorentz変換のもとで同じ形式になる性質をLorentz共変性といいます．方程式がLorentz共変性を備えていれば特殊相対性原理が満たされることになります．

　反変vector場で表された物理量からなる物理法則を，慣性系 $ M(ct,x,y,z)$ において，次のように表します．

$\displaystyle A^{\mu}(x)=0$

一般に，この式の左辺は複数の項からなります．ここで，慣性系 $ M(ct,x,y,z)$ から $ M'(ct',x',y',z')$ へ座標がLorentz変換したとき， $ M'(ct',x',y',z')$ において物理法則が次の形式になれば，Lorentz共変性が満たされていることになります．

$\displaystyle A'^{\mu}(x')=0$

この式の導出は次のように簡潔に実行されます．

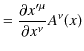$\displaystyle A'^{\mu}(x')$ $\displaystyle =\dfrac{\partial x'^{\mu}}{\partial x^{\nu}}A^{\nu}(x)$    
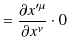  $\displaystyle =\dfrac{\partial x'^{\mu}}{\partial x^{\nu}}\cdot0$    
  $\displaystyle =0$    

以上のことをまとめて，次のように表現しておきます．

$\displaystyle A^{\mu}(x)=0\Rightarrow A'^{\mu}(x')=0$ (4.7)

すなわち，物理法則を表す方程式が反変vector場で構成されているとき，方程式はLorentz共変性を満たし，特殊相対性原理の要請に従うことが保証されます．共変vector場で表された物理量からなる方程式によって表される物理法則がLorentz変換のもとに同じ形式で表されることも同様に，次のように簡潔に表現されます．

$\displaystyle A_{\mu}(x)=0\Rightarrow A'_{\mu}(x')=0$ (4.8)

この式の導出も簡潔にできます．

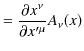$\displaystyle A'_{\mu}(x')$ $\displaystyle =\dfrac{\partial x^{\nu}}{\partial x'^{\mu}}A_{\nu}(x)$    
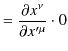  $\displaystyle =\dfrac{\partial x^{\nu}}{\partial x'^{\mu}}\cdot0$    
  $\displaystyle =0$    

すなわち，物理法則を表す方程式が共変vector場で構成されているとき，方程式はLorentz共変性を満たし，特殊相対性原理の要請に従います．

　物理法則が2階反変tensor場，2階共変tensor場で表されても，4元vector場と同様にLorentz共変性を満たすことが保証されています．

  $\displaystyle A^{\mu\nu}(x)=0\Rightarrow A'^{\mu\nu}(x')=0$ (4.9)
  $\displaystyle A_{\mu\nu}(x)=0\Rightarrow A'_{\mu\nu}(x')=0$ (4.10)

導出は4元vector場の場合と全く同様に変換の式から簡潔に実行されます．

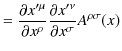$\displaystyle A'^{\mu\nu}(x')$ $\displaystyle =\dfrac{\partial x'^{\mu}}{\partial x^{\rho}}\dfrac{\partial x'^{\nu}}{\partial x^{\sigma}}A^{\rho\sigma}(x)$    
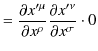  $\displaystyle =\dfrac{\partial x'^{\mu}}{\partial x^{\rho}}\dfrac{\partial x'^{\nu}}{\partial x^{\sigma}}\cdot0$    
  $\displaystyle =0$    

あるいは，

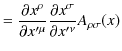$\displaystyle A'_{\mu\nu}(x')$ $\displaystyle =\dfrac{\partial x^{\rho}}{\partial x'^{\mu}}\dfrac{\partial x^{\sigma}}{\partial x'^{\nu}}A_{\rho\sigma}(x)$    
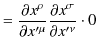  $\displaystyle =\dfrac{\partial x^{\rho}}{\partial x'^{\mu}}\dfrac{\partial x^{\sigma}}{\partial x'^{\nu}}\cdot0$    
  $\displaystyle =0$    

のように証明されます．物理法則を表現する方程式が，反変vector場，共変vector場や2階反変tensor場，2階共変tensor場で記述されていれば，自動的に方程式はLorentz共変性を満たし，特殊相対性原理が満足されます．次の2つのChapterに渡って，具体的に特殊相対論的電磁気学と特殊相対論的力学について見ていくことにしましょう．