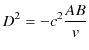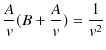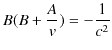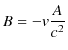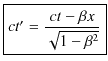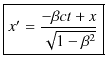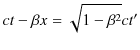Chapter2 Lorentz変換とMinkowski時空
2.1 慣性系とLorentz変換
前Chapterで,特殊相対性原理と光速不変の原理を導入し,特別な慣性系は存在しないことについて言及しました.ただし,特殊相対性理論では,慣性系に限って,議論を進めていきます.全く一般の座標系の場合は,一般相対性理論のPartで取り扱います.慣性系とは,慣性の法則が成立する座標系であると定義されましたね.重力が働いている座標系や,加速運動をしている座標系は慣性系ではありません.これからの議論は,完全な慣性系があるものとして進めていきます.一旦,慣性系が1つ見つかれば,それに対して等速直線運動している無限個の座標系も慣性系になります.そして,全ての慣性系で物理学の法則は,同じ形式で表現されるのでした.特殊相対性理論は慣性系の間の関係について取り扱っていく理論です.
Newton力学では,慣性系の間の座標変換はGalilei変換でした.しかし,Maxwell電磁気学は,Galilei変換に対して成立しませんでした.Maxwell電磁気学でも成立するような,特殊相対性理論で取り扱う,慣性系の間の座標変換をLorentz変換といいます.Lorentz変換がどのように表され,導出されるのか,次のSectionで見ていきましょう.
2.2 Lorentz変換の導出
Lorentz変換を導出しましょう.Galilei変換を導出したときと同じ状況設定をします.つまり,慣性系 ![]() (時間が
(時間が ![]() ,空間成分が
,空間成分が ![]() です.)に対して,
です.)に対して,![]() の正の方向に速さvで等速直線運動している慣性系
の正の方向に速さvで等速直線運動している慣性系 ![]() (時間が
(時間が ![]() ,空間成分が
,空間成分が
![]() です.)を考えます.ただし,ダッシュの付いていない慣性系とダッシュの付いている慣性系は同等な座標系であり,基準となる慣性系はありません.
です.)を考えます.ただし,ダッシュの付いていない慣性系とダッシュの付いている慣性系は同等な座標系であり,基準となる慣性系はありません.
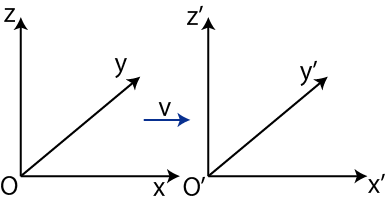
Figure2.1: Lorentz変換1
2つの慣性系が時刻 0 で原点が一致した瞬間に,原点から光のパルス波を発射するものとします.光速不変の原理より,その波面は ![]() に対しても,
に対しても,![]() に対しても,球面状に外向きに一定の速さ
に対しても,球面状に外向きに一定の速さ ![]() で拡がっていきます.したがって,それぞれの光の波面は,球面の方程式である次式を満たします.
で拡がっていきます.したがって,それぞれの光の波面は,球面の方程式である次式を満たします.
この2式を次のように書き直しておきます.
ここで,2つの慣性系の間の座標変換は線形であると仮定します.
![]() 方向と
方向と ![]() 方向は運動していないので,
方向は運動していないので,![]() 成分と
成分と ![]() 成分は不変であるとしました.また,時間も変換すると仮定しました.(前のChapterでの同時性の問題の議論を思い出して下さい.絶対時間の概念は破棄され,時間は観測する座標系によって異なったものでした.)
成分は不変であるとしました.また,時間も変換すると仮定しました.(前のChapterでの同時性の問題の議論を思い出して下さい.絶対時間の概念は破棄され,時間は観測する座標系によって異なったものでした.)![]() は変換の係数です.以下の計算によって決定していきます.
は変換の係数です.以下の計算によって決定していきます.
慣性系 ![]() の原点
の原点 ![]() では,
では,![]() ですが,このとき,
ですが,このとき,![]() となり,
となり,
となります.この式は ![]() の満たす式なので,右辺の
の満たす式なので,右辺の ![]() は
は ![]() に対する
に対する ![]() の速さ
の速さ ![]() になります.したがって,
になります.したがって,
です.故に,
となります.
これらの式を光の波面が満たす方程式(ダッシュのついている(2.2)式)に代入して計算します.
ここで,最後の式と光の波面を表す方程式(ダッシュのついていない(2.1)式)を比較して,次の3式を得ます.
これらの式を ![]() について解きます.(2.4)式より,
について解きます.(2.4)式より,
が得られます.(2.6)式を(2.3)式に代入します.
よって,
です.さらに,(2.6)式を(2.5)式に代入して計算します.
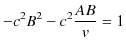
故に,
となります.(2.8)式÷(2.7)式より,
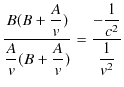 |
||
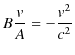 |
となり,よって,
が得られます.(2.9)式を(2.8)式に代入して,
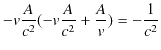 |
||
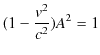 |
||
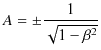 |
(ただし,
と,おきました.)ここで,![]() の極限で
の極限で ![]() となるので,前の符号は正になります.よって,
となるので,前の符号は正になります.よって,
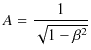
です.(2.9)式より,
 |
||
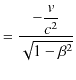 |
となります.また,(2.6)式より,
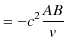 |
||
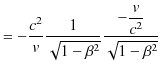 |
||
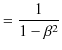 |
となり,故に,
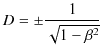
です.ここで,![]() の極限で
の極限で ![]() となるので,前の符号は正になります.よって,
となるので,前の符号は正になります.よって,
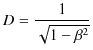
です.以上で,![]() が出揃いました.よって,時間成分の変換は次のようになります.
が出揃いました.よって,時間成分の変換は次のようになります.
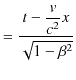 |
ですから,
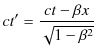
となります.この時間成分を ![]() という量を使って表しています.これは,時間tに光速
という量を使って表しています.これは,時間tに光速 ![]() をかけると式が見やすくなるということと,時間成分も空間成分に合わせて長さの次元にできるという利点があります.また,
をかけると式が見やすくなるということと,時間成分も空間成分に合わせて長さの次元にできるという利点があります.また,
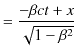 |
となります.ここで,Lorentz変換の式をまとめて書いておきます.時間成分は,
と変換されます.![]() 成分は,
成分は,
と変換されます.![]() 成分は,
成分は,
です.![]() 成分は,
成分は,
です.時間成分も空間成分と同様に変換されていることに注意して下さい.繰り返しますが,相対性理論では絶対時間は否定されます.(Newton力学の変換であるGalilei変換で,![]() となっていたのとは,全く違いますね.)
となっていたのとは,全く違いますね.)
次に,Lorentz逆変換,すなわちダッシュの付かない成分をダッシュの付いた成分で表す式を導いておきましょう.(2.10)式より,
です.故に,
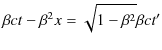
となります.また,(2.11)式より,
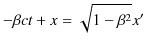
です.これらの式の両辺をそれぞれ加え計算します.
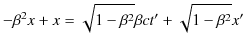 |
||
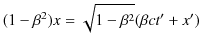 |
||
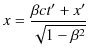 |
また,(2.14)式より,
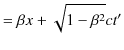 |
||
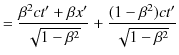 |
||
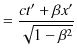 |
となります.Lorentz逆変換をまとめて書くと,
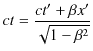 |
(2.15) | |
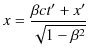 |
(2.16) | |
| (2.17) | ||
| (2.18) |
となります.これらは,Lorentz変換(2.10)式~(2.13)式で,ダッシュを付け替え,vを-vに置き換えたものになっています.このことからも,2つの慣性系が全く同等であることが理解されますね.
2.3 Lorentz変換とGalilei変換の関係
特殊相対性理論の座標変換は,Lorentz変換であることがわかりました.Galilei変換はNewton力学の変換であり,破棄されるべきものです.しかし,慣性系間の速度 ![]() が,光速
が,光速 ![]() に比べて小さいときは,Lorentz変換は近似的にGalilei変換になります.つまり,日常生活の上では,Galilei変換も近似的に成立するのです.計算によってこのことを示しておきましょう.Lorentz変換の時間成分は,
に比べて小さいときは,Lorentz変換は近似的にGalilei変換になります.つまり,日常生活の上では,Galilei変換も近似的に成立するのです.計算によってこのことを示しておきましょう.Lorentz変換の時間成分は,
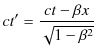
でした.ここで,
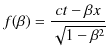
とおき,![]() についてMaclaurin展開します.
についてMaclaurin展開します.
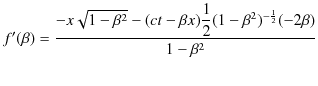
なので,
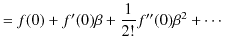 |
||
となります.ただし,![]() の2次以上の項は小さいとして無視しました.このとき,
の2次以上の項は小さいとして無視しました.このとき,
ですから,
となります.確かに,時間成分は近似的にGalilei変換になりました.同様に,![]() 成分も見ておきます.Lorentz変換は,
成分も見ておきます.Lorentz変換は,
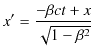
でした.ここで,
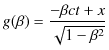
とおき,![]() についてMaclaurin展開します.
についてMaclaurin展開します.
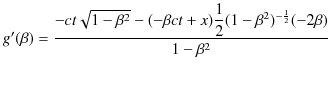
なので,
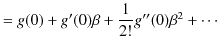 |
||
となります.ただし,![]() の2次以上の項は小さいとして無視しました.このとき,
の2次以上の項は小さいとして無視しました.このとき,
となります.確かに,![]() 成分は近似的にGalilei変換になりました.
成分は近似的にGalilei変換になりました.
一般に,慣性系間の速度 ![]() が光速
が光速 ![]() に比べて小さい場合,特殊相対性理論の結論はNewton力学に近似されます.特殊相対性理論はNewton力学を含んでいると言ってもよいでしょう.
に比べて小さい場合,特殊相対性理論の結論はNewton力学に近似されます.特殊相対性理論はNewton力学を含んでいると言ってもよいでしょう.
2.4 4次元時空と世界点・世界線
Lorentz変換(2.10)式~(2.13)式は時間と空間の成分が混ざった変換式になっています.時間と空間は密接に関係し,切り離して考えることは,もはや不可能です.そこで,これからは時間1次元と空間3次元からなる4次元時空という概念を導入します.慣性系はNewton力学では空間的な概念でしたが,特殊相対性理論では4次元時空の慣性系に進化します.特殊相対性理論における4次元時空の慣性系を,次のように表記します.
(慣性系を表していた ![]() という文字を,
という文字を,![]() に替えました.これは後のSectionで導入するMinkowski時空の頭文字から採りました.)括弧の中の最初の成分は時間についてのものですが,前にも触れたように光速
に替えました.これは後のSectionで導入するMinkowski時空の頭文字から採りました.)括弧の中の最初の成分は時間についてのものですが,前にも触れたように光速 ![]() が掛かっています.この成分を第0成分とします.また,
が掛かっています.この成分を第0成分とします.また,![]() は空間成分ですが,第1,第2,第3成分とします.(空間成分を第1,第2,第3成分とし,時間成分を第4成分とする表記方法もありますが,ここでは第0,第1,第2,第3成分とする方法を採用します.時間成分は第4成分とするよりも,第0成分とした方が,空間成分と見分けることができて考えやすいと思います.)
は空間成分ですが,第1,第2,第3成分とします.(空間成分を第1,第2,第3成分とし,時間成分を第4成分とする表記方法もありますが,ここでは第0,第1,第2,第3成分とする方法を採用します.時間成分は第4成分とするよりも,第0成分とした方が,空間成分と見分けることができて考えやすいと思います.)
フラッシュが光ったとか,物体が速度を変えたとか,2つの物体が衝突した等の物理的な出来事を事象といいます.事象を記述するには,その起こった時間と空間を示さなければなりません.そのために,4次元時空の1点
![]() である世界点というものを導入します.1つの粒子の4次元時空上での世界点の軌跡を世界線と言います.4次元時空のグラフを図示することは不可能なので,縦軸に時間成分
である世界点というものを導入します.1つの粒子の4次元時空上での世界点の軌跡を世界線と言います.4次元時空のグラフを図示することは不可能なので,縦軸に時間成分 ![]() 軸をとり,横軸に空間1成分(
軸をとり,横軸に空間1成分(![]() 成分)をとった,2次元時空図を描いてみます.
成分)をとった,2次元時空図を描いてみます.
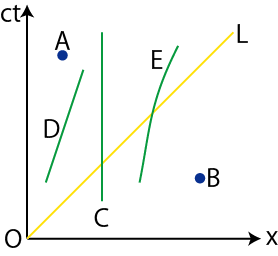
Figure2.2: 世界点と世界線
ここで,![]() と
と ![]() は世界点を示します.世界線
は世界点を示します.世界線 ![]() は静止している粒子を表しています.
は静止している粒子を表しています.![]() 成分が変化せず,時間成分
成分が変化せず,時間成分 ![]() だけが増加していますね.世界線
だけが増加していますね.世界線 ![]() は等速直線運動している粒子を表しています.傾きが一定になっていて等速であることがわかります.
は等速直線運動している粒子を表しています.傾きが一定になっていて等速であることがわかります.![]() は光の世界線です.速さが
は光の世界線です.速さが ![]() ですから,傾きは
ですから,傾きは ![]() になります.(縦軸が
になります.(縦軸が![]() であることに注意して下さい.)世界線
であることに注意して下さい.)世界線 ![]() は任意の運動をしている粒子を表しています.
は任意の運動をしている粒子を表しています.
2.5 Lorentz変換の2次元時空図
2次元時空図においてLorentz変換はどのように図示されるでしょうか? ![]() から
から
![]() へのLorentz変換の式は,
へのLorentz変換の式は,
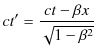 |
||
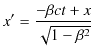 |
と表されます.変換された ![]() 軸は,
軸は,![]() とおいて,
とおいて,
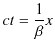 |
となります.また,変換された ![]() 軸は,
軸は,![]() とおいて,
とおいて,
となります.したがって,2次元時空図は図のようになります.
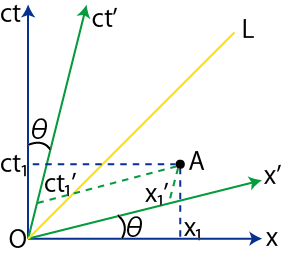
Figure2.3: Lorentz変換2
世界点 ![]() は
は ![]() に対しては
に対しては
![]() ですが,
ですが,![]() に対しては
に対しては
![]() となります.また,図の角
となります.また,図の角 ![]() は,
は,
の関係があります.![]() は光の世界線です.
は光の世界線です.
Lorentz逆変換も2次元時空図で表しておきましょう.変換の式は,
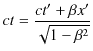 |
||
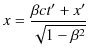 |
でした.変換された ![]() 軸は,
軸は,![]() とおいて,
とおいて,
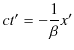 |
となります.また,変換された ![]() 軸は,
軸は,![]() とおいて,
とおいて,
となります.したがって,2次元時空図は図のようになります.
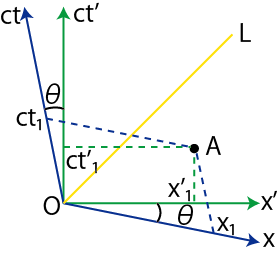
Figure2.4: Lorentz逆変換
世界点 ![]() は
は ![]() に対しては,
に対しては,
![]() ですが,
ですが,![]() に対しては
に対しては
![]() となります.やはり,図の角
となります.やはり,図の角 ![]() は,
は,
の関係があります.![]() は光の世界線です.
は光の世界線です.
2.6 IntervalとMinkowski時空
3次元空間の原点 ![]() と任意の座標
と任意の座標 ![]() の間の距離
の間の距離 ![]() の2乗は3平方の定理より,
の2乗は3平方の定理より,
で表されました.そして,この距離 ![]() の2乗は原点の回りの座標軸の回転に対して値を変えませんでした.(変換の前後で変わらない量を不変量といい,その性質を不変性と言います.)このことは直観的に明らかですが,直接計算によって次のように示すことができます.簡単のため,
の2乗は原点の回りの座標軸の回転に対して値を変えませんでした.(変換の前後で変わらない量を不変量といい,その性質を不変性と言います.)このことは直観的に明らかですが,直接計算によって次のように示すことができます.簡単のため,![]() 軸を軸として,
軸を軸として,![]() 平面を
平面を ![]() だけ反時計回りに回転させます.回転後の座標
だけ反時計回りに回転させます.回転後の座標
![]() は回転前の座標
は回転前の座標 ![]() によって,
によって,
と表されます.したがって,
となります.(証明終.)
4次元時空に対して,この3次元空間の距離 ![]() に相当する量を考えましょう.時間
に相当する量を考えましょう.時間 ![]() で空間座標の原点
で空間座標の原点 ![]() を出発した光の先端が
を出発した光の先端が ![]() 秒後に到達する点の座標の方程式,つまり,光の球面波の式は,
秒後に到達する点の座標の方程式,つまり,光の球面波の式は,
で与えられました.光速不変の原理より,この式が任意の慣性系において成立することから,Lorentz変換は導出されました.この式の左辺の量は,光に対しては常に 0 になりますが,原点
![]() と任意の世界点
と任意の世界点
![]() に対してはある有限の値をとります.そこで,この量を4次元時空における距離の2乗として定義し,その性質を調べることにします.
に対してはある有限の値をとります.そこで,この量を4次元時空における距離の2乗として定義し,その性質を調べることにします.
| (2.19) |
ここで,![]() をintervalと名付けることにします.(世界距離または不変距離とも言います.)Intervalの2乗の式の中には,空間成分の2乗の和に加えて,時間成分の2乗が入ってきています.そして,時間成分の2乗の符号と空間成分の2乗の和の符号は反対になっています.ここでは,時間成分の2乗の符号を正,空間成分の2乗の和の符号を負と定義しました.この定義は逆にしても構いません.要は,intervalはLorentz変換に対して不変であるという大切な性質をもっていればよいのです.これはもともとintervalが不変になるようにLorentz変換を導出したのですから,当然の結論なのですが,次のように直接計算して示すことができます.
をintervalと名付けることにします.(世界距離または不変距離とも言います.)Intervalの2乗の式の中には,空間成分の2乗の和に加えて,時間成分の2乗が入ってきています.そして,時間成分の2乗の符号と空間成分の2乗の和の符号は反対になっています.ここでは,時間成分の2乗の符号を正,空間成分の2乗の和の符号を負と定義しました.この定義は逆にしても構いません.要は,intervalはLorentz変換に対して不変であるという大切な性質をもっていればよいのです.これはもともとintervalが不変になるようにLorentz変換を導出したのですから,当然の結論なのですが,次のように直接計算して示すことができます.
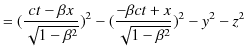 |
||
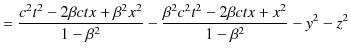 |
||
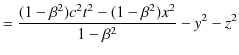 |
||
(証明終.)お互いに等速直線運動する2つの慣性系はLorentz変換で結ばれ,その際intervalは不変です.(これをintervalのLorentz不変性といいます.)IntervalがLorentz不変性をもつ慣性系のことをMinkowski時空と言います.特殊相対性理論における4次元時空はMinkowski時空です.
2.7 Minkowski時空の分類
特殊相対性理論の時空であるMinkowski時空は,intervalの2乗の符号により分類することができます.簡単のため,2次元時空を考えましょう.原点 ![]() と世界点
と世界点 ![]() の間のintervalの2乗は,
の間のintervalの2乗は,
となります.Intervalの2乗が正の値をとるとき,時空は時間的(Time-like)であると言います.このとき,
の関係があります.(2次元時空図での領域は,"Minkowski時空" の図を見て下さい.)時間的な時空において,原点 ![]() と世界点
と世界点 ![]() は因果関係をもつことができます.つまり,影響を及ぼすことのできる関係にあります.次に,intervalの2乗が負の値をとるとき,時空は空間的(Space-like)であるといいます.このとき,
は因果関係をもつことができます.つまり,影響を及ぼすことのできる関係にあります.次に,intervalの2乗が負の値をとるとき,時空は空間的(Space-like)であるといいます.このとき,
の関係があります.(2次元時空図での領域は,"Minkowski時空" の図を見て下さい.)空間的な時空では,原点 ![]() と世界点
と世界点 ![]() は因果関係をもつことができません.(信号は光速を超えることはできません.)最後にintervalの2乗が 0 のとき,時空は光的(Light-like)であると言います.このとき,
は因果関係をもつことができません.(信号は光速を超えることはできません.)最後にintervalの2乗が 0 のとき,時空は光的(Light-like)であると言います.このとき,
の関係があります.(2次元時空図では2本の黄色の直線になります.)光のintervalの2乗は 0 になります.まとめると次のようになります.
- Time-like(
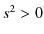 )
) - Space-like(
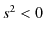 )
) - Light-like(
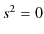 )
)
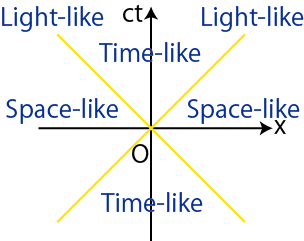
Figure2.5: Minkowski時空
次のChapterでは,特殊相対性理論に従うと,どのような世界になるのか,その非日常的な現象を見ていくことにしましょう.