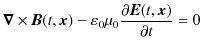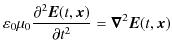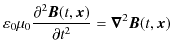Part1 特殊相対性理論

Chapter1 特殊相対性原理と光速不変の原理

1.1 Newton力学（絶対空間・絶対時間，そしてGalilei変換とGalileiの相対性原理）

19世紀までの物理学は，Newton力学とMaxwell電磁気学から構成されていました．特殊相対性理論はこの2つの物理学を土壌として，20世紀初頭にEinsteinによって創始されたのです．（論文として発表されたのは，1905年です．この年は，"奇跡の年" と呼ばれています．）このSectionでは，Newton力学について再考しておきます．特殊相対性理論は物理学の革命であり，Newton力学において根底となっている時間と空間に対する大前提は変更を余儀なくされました．その経緯を，このChapter全体にわたって詳細に見ていきましょう．まず，Newtonの3法則を改めて書き留めておきます．

　第1法則（慣性の法則） "力が働かないか，つりあっているとき，静止している物体は静止を続け，動いている物体は等速直線運動を続けます．"

　第2法則（運動の法則） "力が働くとき，物体には力の向きに加速度が生じます．加速度の大きさは，力の大きさに比例し，質量に反比例します．（数式で表現したものが運動方程式です．）"

　第3法則（作用・反作用の法則） "物体 $ A$ から物体 $ B$ へ力（作用）が働くとき，物体 $ B$ から物体 $ A$ へ，大きさが等しく，向きが反対で，同一作用線上にある力（反作用）が働き返します．"

第3法則はここでは問題とせず，第1法則と第2法則について考えましょう．第2法則の運動方程式があれば，第1法則の慣性の法則は必要ないように思われます．（運動方程式において，力を 0 にすれば，加速度も 0 になり，静止または等速直線運動になります．）しかし，慣性の法則は，その座標系が慣性系というものであるか否かを判定する条件になっています．つまり，慣性系とは，慣性の法則が成立する座標系であると定義されるのです．実際に慣性系を設定することは，思ったよりも難しいものです．すぐに思い付く慣性系の候補として，地球上での摩擦の小さな水平な台の水平方向の運動が挙げられます．しかし，摩擦を完全に取り除くことはできませんし，地球自体が運動しています．ですから，この例は慣性系ではないのです．ここで，宇宙空間を考えましょう．宇宙空間では無重力です．（重力は遠距離力なので，宇宙空間でも完全に 0 にすることはできません．しかし，ここでは，それを無視して考えることにします．）無重力な宇宙空間を浮遊している物体は，確かに慣性の法則に従い，何の力も加えなくてもに等速直線運動を続けることになります．このときの座標系は，近似的に慣性系と見なすことができるでしょう．ここで，物理の常套手段である理想化を行い，完全な慣性系が宇宙にあるものとして，今後の議論を進めることにします．ある慣性系が1つ見つかったとしましょう．それに対して等速直線運動している新しい座標系では，働く慣性力は 0 です．また，もとの慣性系に対して，物体が静止または等速直線運動していれば，新しい座標系に対する物体の運動の状態も，静止，または等速直線運動になることがわかります．したがって，新しい座標系も慣性系ということになります．もとの慣性系に対する新しい慣性系の速度は，等速度である限り，向きと大きさは任意です．したがって，新しく考えられる慣性系は無限個存在します．強調して書き留めておきましょう．

　"一旦，理想化された慣性系が1つ見つかれば，それに対して等速直線運動している無限個の座標系も慣性系になります．"

　ここで，基本的な事項ですが，絶対と相対という言葉の意味を考えておきましょう．絶対という言葉は，何か基準になるものが存在する場合に使います．例えば，"地面を基準として，ビルの5階は $ 20[m]$ の高さです．" と言った場合，地面からの高さというものは絶対的な量になります．それに対して，相対という言葉は，2つのもの $ A$，$ B$ があり，$ A$ に対する $ B$ の量とか，逆に $ B$ に対する $ A$ の量というものを考える場合に使います．例えば，"ビルの3階に対する7階の高さは $ 16[m]$ です．" と言った場合，3階に対する7階の高さという，あいたいする量を考えていますので，相対的な量ということになります．ここで，問題となるのが，慣性系は絶対的なものなのか？ それとも，相対的なものなのか？ ということです．言葉を変えて言うと，何か基準となる絶対的な慣性系が1つ存在していて，それに対して等速直線運動している無限個の慣性系が存在するのか？ それとも，基準となる慣性系というものは存在せず，無限個の慣性系は，全て同等で，あいたいする存在なのか？ ということです．結論を言うと，Newton力学では，慣性系には基準となる空間と時間が存在するということを大前提としています．お互いに等速直線運動する無限個の慣性系のうち，基準となる空間は絶対空間と言い，宇宙の重心を原点にとり，Descartes座標の $ x$ 軸，$ y$ 軸，$ z$ 軸を無限に伸ばして設定します．そして，Newton力学での時間は絶対時間と言い，全ての慣性系で共通であり，無限の過去から無限の未来に向かって一様に流れるものです．Newton力学の前提として，絶対空間と絶対時間が設定された理由は，それが，誰もが当然と思っている空間と時間の概念だからでした．宇宙空間として基準となるものが1つだけ存在し，その入れ物の中で，唯一の時間が過去から未来に向かって流れているという描像は常識として受け入れやすいものです．

　さて，ある慣性系 $ S$ が見つかったとします．$ S$ は絶対空間でもよいですし，それに対して等速直線運動している無限個の慣性系のうちの1つでもよいです．その慣性系 $ S$ の座標を $ (x,y,z)$，時間を $ t$ とします．慣性系 $ S$ では，Newtonの運動方程式，

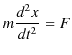
$\displaystyle m\dfrac{d^{2}x}{dt^{2}}=F$

が成立します．ここで，$ S$ に対して，$ x$ の正の方向に速さ $ v$ で等速直線運動している慣性系 $ S'$ を考えて，その座標を， $ (x',y',z')$，その時間を $ t'$ としましょう．（簡単のため，$ x$ 方向にのみ運動しているとしました．また，$ t=t'=0$ で2つの座標系の原点が重なっているとします．）

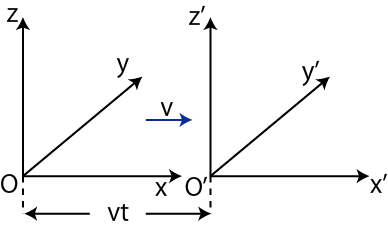
Galilei変換

Figure1.1: Galilei変換

このとき，$ t'$ と $ (x',y',z')$ の成分を $ t$ と $ (x,y,z)$ の成分で表すと，次のようになります．

  $\displaystyle t'=t$    
  $\displaystyle x'=x-vt$    
  $\displaystyle y'=y$    
  $\displaystyle z'=z$    

Newton力学では，時間は絶対時間ですから，2つの座標系で時間は共通になるとしました．（このことは，当然と思われるかもしれませんが，実は特殊相対性理論では変更されます．後のSectionを見て下さい．）$ x$ 成分は $ vt$ を引いています．これは，ダッシュの付く座標 $ x'$ は，原点が $ vt$ だけ正の方向に動いた分，ダッシュの付かない座標 $ x$ より，小さくなっているからです．$ y$ 成分と $ z$ 成分は，座標系が動いていませんので変わりません．以上のような座標変換のことをGalilei変換と言います．Galilei変換において，空間成分を時間 $ t=t'$ で微分すると，

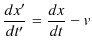  $\displaystyle \dfrac{dx'}{dt'}=\dfrac{dx}{dt}-v$    
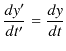  $\displaystyle \dfrac{dy'}{dt'}=\dfrac{dy}{dt}$    
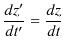  $\displaystyle \dfrac{dz'}{dt'}=\dfrac{dz}{dt}$    

となります．もう1回，時間 $ t=t'$ で微分すると，

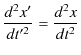  $\displaystyle \dfrac{d^{2}x'}{dt'^{2}}=\dfrac{d^{2}x}{dt^{2}}$    
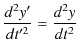  $\displaystyle \dfrac{d^{2}y'}{dt'^{2}}=\dfrac{d^{2}y}{dt^{2}}$    
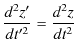  $\displaystyle \dfrac{d^{2}z'}{dt'^{2}}=\dfrac{d^{2}z}{dt^{2}}$    

となります．また，力 $ F$ は絶対的な物理量であり，あたらしい慣性系でも同じであるとします．すなわち，

$\displaystyle F'=F$

です．慣性系 $ S$ では，Newtonの運動方程式，

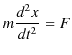
$\displaystyle m\dfrac{d^{2}x}{dt^{2}}=F$

が成立しました．このとき，上の関係より，新しい座標系 $ S'$ でも，運動方程式が成立することが確認されます．

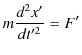
$\displaystyle m\dfrac{d^{2}x'}{dt'^{2}}=F'$

このように，ある慣性系で物理法則が成立するとき，Galilei変換した別の慣性系でも同じ形式で物理法則が成立することを，Galileiの相対性原理といいます．Newton力学では，Galileiの相対性原理が成立することがわかりました．

　Newton力学は，常識的な観点からも，Galileiの相対性原理が成立する点から考えても，矛盾はなく，何の問題もないように思われます．次に，Maxwell電磁気学を考えていきましょう．

 

1.2 Maxwell電磁気学（新しい座標変換と新しい相対性原理の可能性）

19世紀までの物理学のもう1つの柱であるMaxwell電磁気学について考察していくことにしましょう．簡単な電磁気学的現象例を取り上げると，コイルと棒磁石を使った電磁誘導の実験をする際，その相対的な運動のみが問題となります．つまり，コイルが静止していて棒磁石が動いていても，棒磁石が静止していてコイルが動いていても，その差異は認められません．すなわち，空間とは相対的なものではないのでしょうか？ それとも，絶対空間が存在するのでしょうか？ また，時間についてはどのようなことが言えるのでしょうか？ 議論を始めましょう．電磁気学の基礎方程式であるMaxwell方程式とは，次の4式でした．

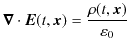  $\displaystyle \bm{\nabla}\cdot\bm{E}(t,\bm{x})=\dfrac{\rho(t,\bm{x})}{\varepsilon_{0}}$    
  $\displaystyle \bm{\nabla}\cdot\bm{B}(t,\bm{x})=0$    
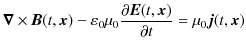  $\displaystyle \bm{\nabla}\times\bm{B}(t,\bm{x})-\varepsilon_{0}\mu_{0}\dfrac{\partial\bm{E}(t,\bm{x})}{\partial t}=\mu_{0}\bm{j}(t,\bm{x})$    
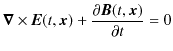  $\displaystyle \bm{\nabla}\times\bm{E}(t,\bm{x})+\dfrac{\partial\bm{B}(t,\bm{x})}{\partial t}=0$    

ここで，電荷密度 $ \rho(t,\bm{x})$ と電流密度 $ \bm{j}(t,\bm{x})$ が 0であるような真空の空間領域を考えると，Maxwell方程式は次のようになります．

  $\displaystyle \bm{\nabla}\cdot\bm{E}(t,\bm{x})=0$ (1.1)
  $\displaystyle \bm{\nabla}\cdot\bm{B}(t,\bm{x})=0$ (1.2)
  $\displaystyle \bm{\nabla}\times\bm{B}(t,\bm{x})-\varepsilon_{0}\mu_{0}\dfrac{\partial\bm{E}(t,\bm{x})}{\partial t}=0$ (1.3)
  $\displaystyle \bm{\nabla}\times\bm{E}(t,\bm{x})+\dfrac{\partial\bm{B}(t,\bm{x})}{\partial t}=0$ (1.4)

これらの真空中でのMaxwell方程式から，まず，電場 $ \bm{E}(t,\bm{x})$ の満たす方程式を導きます．(1.4)式に左から $ \bm{\nabla}\times$ をかけます．（回転をとります．）

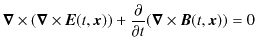
$\displaystyle \bm{\nabla}\times(\bm{\nabla}\times\bm{E}(t,\bm{x}))+\dfrac{\partial}{\partial t}(\bm{\nabla}\times\bm{B}(t,\bm{x}))=0$

ここで，ベクトル解析の公式，

$\displaystyle \bm{\nabla}\times(\bm{\nabla}\times\bm{A})=\bm{\nabla}(\bm{\nabla}\cdot\bm{A})-\bm{\nabla}^{2}\bm{A}$

より，

$\displaystyle \bm{\nabla}\times(\bm{\nabla}\times\bm{E}(t,\bm{x}))$ $\displaystyle =\bm{\nabla}(\bm{\nabla}\cdot\bm{E}(t,\bm{x}))-\bm{\nabla}^{2}\bm{E}(t,\bm{x})$    
  $\displaystyle =-\bm{\nabla}^{2}\bm{E}(t,\bm{x})$    

となります．最後の変形は(1.1)式を用いました．さらに，(1.3)式より，

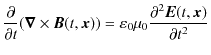
$\displaystyle \dfrac{\partial}{\partial t}(\bm{\nabla}\times\bm{B}(t,\bm{x}))=\varepsilon_{0}\mu_{0}\dfrac{\partial^{2}\bm{E}(t,\bm{x})}{\partial t^{2}}$

ですから， $ \bm{E}(t,\bm{x})$ の満たす方程式は，

$\displaystyle \varepsilon_{0}\mu_{0}\dfrac{\partial^{2}\bm{E}(t,\bm{x})}{\partial t^{2}}=\bm{\nabla}^{2}\bm{E}(t,\bm{x})$ (1.5)

となります．同様な計算により，磁束密度 $ \bm{B}(t,\bm{x})$ の満たす方程式は，

$\displaystyle \varepsilon_{0}\mu_{0}\dfrac{\partial^{2}\bm{B}(t,\bm{x})}{\partial t^{2}}=\bm{\nabla}^{2}\bm{B}(t,\bm{x})$ (1.6)

となることが確かめられます．(1.5)式と(1.6)式は，3次元波動方程式，

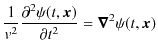
$\displaystyle \dfrac{1}{v^{2}}\dfrac{\partial^{2}\psi(t,\bm{x})}{\partial t^{2}}=\bm{\nabla}^{2}\psi(t,\bm{x})$

と同形になっていることに注意しましょう．ここで， $ \psi(t,\bm{x})$ は波動のもつ一般量（水波の場合は変位を表します．今の場合は電場 $ \bm{E}(t,\bm{x})$ や磁場 $ \bm{B}(t,\bm{x})$ になります．），$ v$ は波動の速さを表します．つまり，電場と磁場は波動として，空間を伝搬する性質をもっていることが理解されます．そして，電場と磁場の波動を電磁波と名付けたのでしたね．このとき，電磁波の速さ $ c$ は，

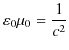
$\displaystyle \varepsilon_{0}\mu_{0}=\dfrac{1}{c^{2}}$

より，

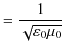$\displaystyle c$ $\displaystyle =\dfrac{1}{\sqrt{\varepsilon_{0}\mu_{0}}}$    
  $\displaystyle \cong\dfrac{1}{\sqrt{8.8541878\times10^{-12}[F\cdot m^{-1}]\times4\pi(=3.14159265)\times10^{-7}[N\cdot A^{-2}]}}$    
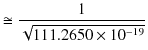  $\displaystyle \cong\dfrac{1}{\sqrt{111.2650\times10^{-19}}}$    
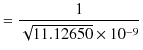  $\displaystyle =\dfrac{1}{\sqrt{11.12650}\times10^{-9}}$    
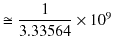  $\displaystyle \cong\dfrac{1}{3.33564}\times10^{9}$    
  $\displaystyle \cong0.29979\times10^{9}$    
  $\displaystyle \cong2.998\times10^{8}[m/s]$    

となります．これが光速と一致することから，光は電磁波の一種であることが判明したのでした．

　ここで問題となるのが，この光速 $ c$ はどの慣性系から観測されたものであるかということです．基準となる慣性系である絶対空間から測定されるものとしてみましょう．Newton力学ではGalileiの相対性原理が成立しましたので，絶対空間に対して，等速直線運動している慣性系についても，運動方程式が成立しました．しかし，Maxwell電磁気学に対してもGalilei変換を適用しようとすると，絶対空間に対する光速 $ c$ は，新しい慣性系に対しては光速は $ c$ ではなくなってまいます．Maxwell方程式の結論である波動方程式(1.5)式と(1.6)式では，光速は唯一 $ c$ です．したがって，Maxwell方程式は，Galilei変換に対して成立しないという結論になります．言葉を換えて言うと，Maxwell電磁気学に対しては，Galileiの相対性原理が成り立たないのです．Maxwell電磁気学が成立するのは，絶対空間に対してのみとなります．Maxwell電磁気学の結論である電磁波の存在にとって，空間には電磁波を伝搬する媒質が必要でした．星の光が宇宙空間を隔てて届くことからわかるように，電磁波は真空中でも伝わります．そこで，考え出されたのがEtherと呼ばれる媒質です．Etherは物質の運動を妨げることはありませんが，電磁波を伝搬する媒質としての性質をもったもので，全宇宙の重心を基準とした絶対空間に対して静止し，空気中，物質中，真空中を問わず，満ち溢れているものと考えられました．上の議論で，光速 $ c$ は絶対空間に対する速さということでしたが，ということは，絶対空間の中で静止しているEtherに対するものだということになります．

　しかしながら，絶対空間とその中に静止しているEtherに対してのみ成立する電磁気学は，美しさの点から承認しがたいものがあります．全ての慣性系で成立する電磁気学の可能性を考えなくてはいけません．Maxwell方程式が，Galilei変換に対して成立しないのならば，新しい座標変換，新しい相対性原理を考えることはできないのでしょうか．問題を整理しましょう．次の2つの立場が考えられます．

  1. 基準となる絶対空間と唯一の絶対時間が存在します．絶対空間とそれに対して等速直線運動する無限個の慣性系に関するGalilei変換を考えた場合，Newton力学についてはGalileiの相対性原理が成立します．また，Maxwell電磁気学は，絶対空間に対して静止しているEtherに対してのみ成立し，それ以外の慣性系では成立しません．つまり，Maxwell電磁気学については，Galileiの相対性原理が成立しません．（絶対空間に対して光速は 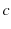$ c$ で，絶対空間に対して等速直線運動している慣性系に対しては，光速は変化します．）
  2. Maxwell電磁気学が全ての慣性系について成立するような，新しい座標変換が存在します．したがって，電磁波の波動方程式が全ての慣性系に対して成立するので，全ての慣性系に対して，光速は唯一 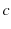$ c$ です．その場合，絶対空間とEtherの存在は否定されます．また，新しい座標変換に対して，Newton力学が成立するか，否か，検討しなければなりません．

Einsteinは後者の立場をとり，特殊相対性理論を創りました．その根拠となる実験を次のSectionで見ていくことにしましょう．（ただし，Einsteinは実験の結果を知らなくても，理論の美しさの観点から同じ結論を見出したと思われます．）

 

1.3 Michelson-Morleyの実験（絶対空間・Etherの概念の破棄から相対的な空間へ）

ここで，絶対空間とEtherの存在について決定的な判決を下したのが，1887年に行われたMichelson-Morleyの実験です．その当時，絶対空間の考え方が主流であったので，この実験は絶対空間に静止しているEtherに対する地球の運動を検出することが当初の目的でした．以下の議論は絶対空間を想定して行いますので，混乱しないようにして下さい．実験装置は図のようになります．

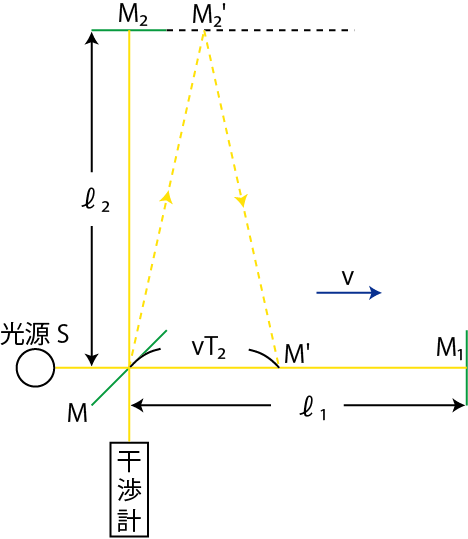
Michelson-Morleyの実験

Figure1.2: Michelson-Morleyの実験

光源 $ S$ から出た光の一部は，半透明の鏡 $ M$ を通過して直進し，鏡 $ M_{1}$ で反射されて再び $ M$ に戻り，ここで反射されて干渉計に入ります．また，光源 $ S$ から出た光の残りは，半透明の鏡 $ M$ により反射されて鏡 $ M_{2}$ へ向かい，ここで $ M_{2}$ に反射されて再び $ M$ に戻り，$ M$ を通り抜けて干渉計に入ります．はじめの光を $ L_{1}$，あとの光を $ L_{2}$ と呼べば，$ L_{1}$ と $ L_{2}$ は干渉します．絶対空間に静止しているEtherから見たとき，装置全体が $ MM_{1}$ の方向に地球とともに一定の速さ $ v$ で運動する場合を考えます．絶対空間では，光は全ての方向にEtherに対して $ c$ の速さで伝わるはずです．したがって，$ L_{1}$ の場合，行きの光の速さは $ c-v$ であり，帰りの光の速さは $ c+v$ になります．故に，光が $ MM_{1}$ を往復する時間 $ T_{1}$ は，

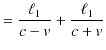$\displaystyle T_{1}$ $\displaystyle =\dfrac{\ell_{1}}{c-v}+\dfrac{\ell_{1}}{c+v}$    
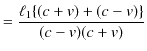  $\displaystyle =\dfrac{\ell_{1}\{(c+v)+(c-v)\}}{(c-v)(c+v)}$    
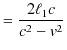  $\displaystyle =\dfrac{2\ell_{1}c}{c^{2}-v^{2}}$    

ですから，

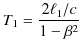
$\displaystyle T_{1}=\dfrac{2\ell_{1}/c}{1-\beta^{2}}$

となります．ただし，$ \beta$ は，

$\displaystyle \beta\equiv\dfrac{v}{c}$

で定義します．$ L_{2}$ について言えば，装置全体の速度は $ MM_{2}$ 方向については 0 なので，光の速さは $ c$ です．ただし，光の走った道筋は $ MM_{2}'M$ なので，そのとき経過した時間 $ T_{2}$ は，

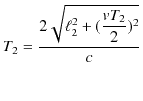
$\displaystyle T_{2}=\dfrac{2\sqrt{\ell_{2}^{2}+(\dfrac{vT_{2}}{2})^{2}}}{c}$

より，

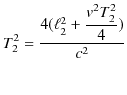  $\displaystyle T_{2}^{2}=\dfrac{4(\ell_{2}^{2}+\dfrac{v^{2}T_{2}^{2}}{4})}{c^{2}}$    
% latex2html id marker 1459 $\displaystyle \therefore$ $\displaystyle c^{2}T_{2}^{2}=4\ell_{2}^{2}+v^{2}T_{2}^{2}$    
% latex2html id marker 1461 $\displaystyle \therefore$ $\displaystyle (c^{2}-v^{2})T_{2}^{2}=4\ell_{2}^{2}$    
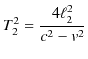% latex2html id marker 1463 $\displaystyle \therefore$ $\displaystyle T_{2}^{2}=\dfrac{4\ell_{2}^{2}}{c^{2}-v^{2}}$    
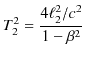% latex2html id marker 1465 $\displaystyle \therefore$ $\displaystyle T_{2}^{2}=\dfrac{4\ell_{2}^{2}/c^{2}}{1-\beta^{2}}$    
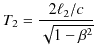% latex2html id marker 1467 $\displaystyle \therefore$ $\displaystyle T_{2}=\dfrac{2\ell_{2}/c}{\sqrt{1-\beta^{2}}}$    

となります．よって，2つの光の時間差 $ \Delta T$ は，

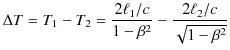
$\displaystyle \Delta T=T_{1}-T_{2}=\dfrac{2\ell_{1}/c}{1-\beta^{2}}-\dfrac{2\ell_{2}/c}{\sqrt{1-\beta^{2}}}$

となります．ここで，装置全体を，$ M$ を中心として時計回りに $ 90^{\circ}$ 回転して同じ実験をします．このとき，$ MM_{2}$ が地球の運動の向きに一致して，$ MM_{1}$ は運動の向きと垂直になります．したがって，この場合の時間差 $ \Delta T'$ は，

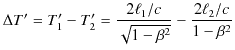
$\displaystyle \Delta T'=T_{1}'-T_{2}'=\dfrac{2\ell_{1}/c}{\sqrt{1-\beta^{2}}}-\dfrac{2\ell_{2}/c}{1-\beta^{2}}$

と求められます．この2つの実験の光の往復時間の差は，

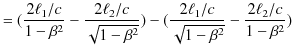$\displaystyle \Delta T-\Delta T'$ $\displaystyle =(\dfrac{2\ell_{1}/c}{1-\beta^{2}}-\dfrac{2\ell_{2}/c}{\sqrt{1-\b... ...}}})-(\dfrac{2\ell_{1}/c}{\sqrt{1-\beta^{2}}}-\dfrac{2\ell_{2}/c}{1-\beta^{2}})$    
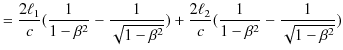  $\displaystyle =\dfrac{2\ell_{1}}{c}(\dfrac{1}{1-\beta^{2}}-\dfrac{1}{\sqrt{1-\b... ...}}})+\dfrac{2\ell_{2}}{c}(\dfrac{1}{1-\beta^{2}}-\dfrac{1}{\sqrt{1-\beta^{2}}})$    
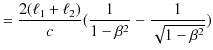  $\displaystyle =\dfrac{2(\ell_{1}+\ell_{2})}{c}(\dfrac{1}{1-\beta^{2}}-\dfrac{1}{\sqrt{1-\beta^{2}}})$    
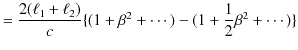  $\displaystyle =\dfrac{2(\ell_{1}+\ell_{2})}{c}\{(1+\beta^{2}+\cdots)-(1+\dfrac{1}{2}\beta^{2}+\cdots)\}$    
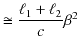  $\displaystyle \cong\dfrac{\ell_{1}+\ell_{2}}{c}\beta^{2}$    

と計算されます．よって， $ 90^{\circ}$ の回転により光路差の変化，

$\displaystyle c(\Delta T-\Delta T')\cong(\ell_{1}+\ell_{2})\beta^{2}$

に相当する干渉縞の移動が起こるはずです．ここで，太陽の周りの地球の公転速度は，

$\displaystyle v\cong3\times10^{4}[m/s]$

であり，光速は，

$\displaystyle c\cong3\times10^{8}[m/s]$

なので，

$\displaystyle \beta=\dfrac{v}{c}\cong10^{-4}$

となります．また，Michelson-Morleyの装置では，

$\displaystyle \ell_{1}\cong\ell_{2}\cong11[m]$

であったので，光路差の変化は，

$\displaystyle (\ell_{1}+\ell_{2})\beta^{2}=(11+11)\times(10^{-4})^{2}=22\times10^{-8}=2.2\times10^{-7}[m]$

となります．しかし，MichelsonとMorleyの結果は，実験値が上の理論値よりもずっと小さいことを示していました．地球のEtherに対する運動は検出されなかったのです．1つの可能性としては，地球がEtherに対して静止していることも考えられますが，太陽の周りを公転していることを考慮すると，そのアイディアは捨てなければなりません．残る選択肢は，絶対空間とその中にあるEtherの存在を否定するしかありません．

　このようにして，基準となる絶対空間が存在せず，全て同等な相対的な空間を考えていく必要が生じました．Einsteinは空間が相対的であるとしたのに留まらず，時間と空間との関係についても再考しました．次の節から特殊相対性理論の原理について考えていきましょう．

 

1.4 特殊相対性原理と光速不変の原理

1905年，Einsteinは19世紀までの物理学と決別するべく，特殊相対性理論を発表しました．Newton力学とMaxwell電磁気学の2つの理論を足がかりとして，革命的な理論に創りなおしたのです．その理論の核心となる2つの原理を，以下に見ていきましょう．

　特殊相対性理論では，慣性系の場合を考えます．このことは，特殊という言葉を使用する理由になっています．特殊相対性理論では，全ての慣性系は相対的です．つまり，特別な慣性系は存在せず，お互いに等速直線運動をしているあらゆる慣性系は同等になります．さらに，特殊相対性理論ではそれ以上のことを主張します．すなわち，全ての物理法則にとって，あらゆる慣性系は同等であるということです．このことをEinsteinは原理として採用しました．

原理1.1(特殊相対性原理) "物理法則は全ての慣性系において，同じ形式で表現されます．"

この原理を特殊相対性原理といいます．Newton力学の法則を表す方程式も，電磁気学の法則を表すMaxwell方程式も，同じ形式で表現されることを要請したのです．（後に，量子力学，場の量子論，弦理論の法則も含むように拡張されました．）具体的に特殊相対性原理を満たす座標変換を考えなくてはなりません．前述したように，Galilei変換は，Newton力学の運動方程式に対しては相対性原理を満たしますが，Maxwell方程式の形を変えてしまいますので，要求を満たしていません．新しい座標変換を考えなくてはなりませんが，次のChapterで導入していきます．

　特殊相対性理論にはもう1つ原理があります．Einsteinは10代半ばの頃，次のようなことを考えていたといいます．すなわち，光速で運動している人は鏡で自分の顔を見ることができるであろうか，という疑問です．顔から出た光は，その人が光速で追いかけているので，速さ 0 になり，鏡では見ることができないのではないでしょうか？ あるいは特別なことが起こるのでしょうか？ ここで，この疑問に答えるために，上記の特殊相対性原理を前述のMaxwell電磁気学について考えてみます．電磁気学の基本法則は4式のMaxwell方程式ですが，特殊相対性原理より全ての慣性系で同じ形式の方程式になると結論付けられます．よって，Maxwell方程式から導出される波動方程式も，全ての慣性系で同じ形式の方程式になります．実際に，変換後の慣性系での波動方程式を書き留めておくと，

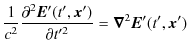  $\displaystyle \dfrac{1}{c^{2}}\dfrac{\partial^{2}\bm{E}'(t',\bm{x}')}{\partial t'^{2}}=\bm{\nabla}^{2}\bm{E}'(t',\bm{x}')$    
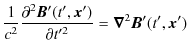  $\displaystyle \dfrac{1}{c^{2}}\dfrac{\partial^{2}\bm{B}'(t',\bm{x}')}{\partial t'^{2}}=\bm{\nabla}^{2}\bm{B}'(t',\bm{x}')$    

です．ダッシュが付いているのは，変換後の座標における量であることを示しています．ここで，波動方程式には光速 $ c$ が含まれていて，同形の波動方程式から計算されるので，全ての慣性系において光速は同じ値になることが理解されます．この結論は常識とは相容れませんが，Einsteinは原理として採用しました．（特殊相対性理論の原理は計2つです．）

原理1.2(光速不変の原理) "光速は全ての慣性系において一定値 $ c$ です．"

この原理を光速不変の原理といいます．（この原理によれば，自分の顔は見えることになりますね．）

 

1.5 同時性の問題（絶対時間の概念の破棄から相対的な時間へ）

光速不変の原理を認めると，事象が同時に起こるということについて，常識では考えられない結論が得られます．例として，等速直線運動している列車の中央でフラッシュを発した場合を考えます．列車の中にいる観測者にとって，光速は一定値 $ c$ です．この観測者にとって，光のパルス波は同時に列車の両端に到着します．（図の "同時性1" を参照してください．）

同時性1

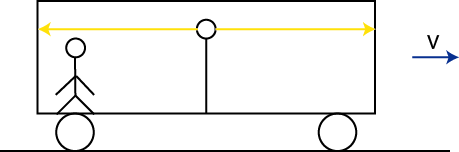
Figure1.3: 同時性1

一方，光速不変の原理から，地面にいる観測者にとっても光速は一定値 $ c$ です．列車は前方に運動しているので，光のパルス波は前方の端よりも後方の端に早く到着することになります.（図の "同時性2" を参考にして下さい．）

同時性2

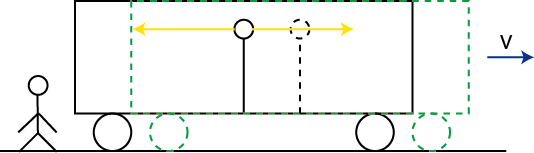
Figure1.4: 同時性2

列車の中の観測者にとって同時である出来事が，地面にいる観測者にとっては同時ではなくなります．もちろん，列車の速度は光速に比較して小さいので，この結論はほとんど無視できます．しかしながら，原理的には同時性が破れているのです．

　列車の中の観測者にとっての同時ということと，地面にいる観測者にとっての同時ということは違うことが理解できました．言い直すと，列車に固定した座標系と，地面に固定した座標系では同時性が異なるということです．さらに話を進めると，時間というものは観測する座標系によって異なったものである，ということまで考えることができます．全ての座標系で共通の絶対時間という概念は破棄される運命にあるのです．空間とともに，時間も相対的なものであることが理解されます．