Chapter2 力
2.1 いろいろな力
力の概念は,本来腕力から派生したもののようです.力は物体を変形させたり,物体の運動を変化させたりする原因になっています.
身近な力の例を幾つか挙げておきましょう.まず,地球から引かれる力である重力があります.2番目の例として,物体が水平面,斜面,あるいは曲面上にあるとき,その面から垂直に働く力が挙げられます.この力を垂直抗力といいます.垂直抗力は何故働くのでしょうか?物体も面も何の変化もないように思えます.実は物体を面の上に置いたとき,物体も面も僅かですが変形しているのです.その歪みをもとに戻そうとする力が垂直抗力の原因となっています.
3番目の例として,糸が張った状態にあるとき,糸に働いている力である糸の張力が挙げられます.糸の張力の原因も垂直抗力に似ていますが,糸の僅かな歪みによるものです.糸は引っ張られたら少しだけ伸びます.伸びたら縮もうとして張力が働くのです.ここで,軽い糸の場合,全ての位置で同じ大きさの張力が働くことについて言及しておきます.(軽いという言葉は,質量が無視できるという意味で使っています.)このことを証明します.まず,糸を短い部分に分割して考えます.分割したある部分に着目すると,その部分は左右に引かれています.その張力の大きさを,それぞれ ![]() と
と ![]() とします.(図を参照して下さい.)
とします.(図を参照して下さい.)
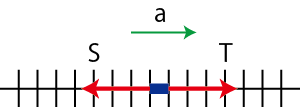
Figure2.1: 張力
このとき運動方程式 ![]() は,
は,
となり,直ちに ![]() が導かれます.この議論を糸の全ての部分に適用すると,全ての位置で同じ大きさの張力が働くことが理解されます.
が導かれます.この議論を糸の全ての部分に適用すると,全ての位置で同じ大きさの張力が働くことが理解されます.
4番目の例として,ばねの弾性力が挙げられます.ばねの弾性力の大きさ ![]() は,ばねの伸びまたは縮み
は,ばねの伸びまたは縮み ![]() に比例します.これをフックの法則と言います.
に比例します.これをフックの法則と言います.
ここで,![]() は比例定数でばね定数と言います.
は比例定数でばね定数と言います.
5番目の例として,摩擦力を挙げておきます.摩擦力は物体が面の上にあるとき,その面が粗いときに受ける力です.(理想的には摩擦を受けないなめらかな面というものを考えることができますが,現実にはなめらかな面は存在せず,粗い面しかありません.)物体が静止している場合の摩擦力は静止摩擦力と言います.物体が動き出す直前のギリギリの状態では,最も大きな静止摩擦力が働きますが,これを最大静止摩擦力(大きさを![]() とします.)と言います.このとき,
とします.)と言います.このとき,![]() は垂直抗力の大きさ
は垂直抗力の大きさ![]() に比例します.
に比例します.
ただし,![]() は比例定数で静止摩擦係数と言います.
は比例定数で静止摩擦係数と言います.![]() は面の状態によって決まります.また,物体が動いている場合に働く摩擦力のことを動摩擦力と言います.動摩擦力の大きさ
は面の状態によって決まります.また,物体が動いている場合に働く摩擦力のことを動摩擦力と言います.動摩擦力の大きさ ![]() も垂直抗力の大きさ
も垂直抗力の大きさ ![]() に比例します.
に比例します.
ただし,![]() は比例定数で動摩擦係数と言います.
は比例定数で動摩擦係数と言います.![]() も接触面によって決まります.一般に,最大静止摩擦力の方が動摩擦力よりも大きくなります.すなわち,
も接触面によって決まります.一般に,最大静止摩擦力の方が動摩擦力よりも大きくなります.すなわち,
です.
最後の例として,浮力を挙げておきます.例えば,水中に物体が沈んでいるとき,物体には上の面からも,側面からも,下の面からも,パスカルの原理に従い面に垂直に水圧が働きます.水圧は水深が深い程大きいので,下の面からの圧力の方が,上の面からの圧力よりも大きいのです.差し引き,上への力が生じます.これが浮力です.(側面に働く圧力は打ち消し合います.)
2.2 力の本質-4つの相互作用
腕力をはじめ,上に挙げたように身近な力はいろいろとありますが,現代の素粒子論では力は次の4つに分類されます.
- 重力(万有引力)
- 電磁力
- 強い力(核力)
- 弱い力
森羅万象において,この4つの力が全ての原因になります.この中で,身近な力は重力と電磁力です.また,腕力や垂直抗力,糸の張力,弾性力,摩擦力,浮力等,身近な大抵の力は,原子分子レベルでの電磁力に帰着されます.強い力と弱い力は素粒子の現象において重要となる力です.素粒子論の立場では4つの力は4つの相互作用と呼ばれます.
2.3 力の合成・分解と力のつりあい
2つの力と同等な1つの力を求めることを力の合成といい,合成された力を合力と言います.逆に,1つの力と同等な2つの力を求めることを力の分解といい,分解された力を分力と言います.ベクトルである力の合成または分解の方法は平行四辺形を描いて求めます.これらは,やはりベクトルである速度の合成・分解と同じような方法になります.
1つの物体にはたらく2力が,大きさが同じで,向きが反対で,同一作用線上にあるとき,力はつりあっていると言います.3力以上の力のつりあいも,幾つかの力を合成することにより,2力のつりあいに帰着されます.
2.4 作用・反作用
2つ物体があって,物体 ![]() が物体
が物体 ![]() に力を及ぼすとき,物体
に力を及ぼすとき,物体 ![]() は物体
は物体 ![]() に力を及ぼしかえします.これを作用・反作用の法則といいます.その際,作用・反作用の2力は大きさが同じで,向きが反対で,同一作用線上にあります.例えば,手で壁を押すと壁は手を押し返します.手でばねを引くと,ばねは弾性力により手を引き返します.2つの電荷の間にはたらくクーロン力はお互いに引き合うか,または,反発しあいます.このように,いかなる場合も作用・反作用の法則は成立するのです.
に力を及ぼしかえします.これを作用・反作用の法則といいます.その際,作用・反作用の2力は大きさが同じで,向きが反対で,同一作用線上にあります.例えば,手で壁を押すと壁は手を押し返します.手でばねを引くと,ばねは弾性力により手を引き返します.2つの電荷の間にはたらくクーロン力はお互いに引き合うか,または,反発しあいます.このように,いかなる場合も作用・反作用の法則は成立するのです.
また,つりありの2力と作用・反作用の2力は成立する3つの条件は同じですが,全く別物の2力であることに注意しましょう.つりあいの2力は同じ1つの物体にはたらく2力が,上記の3つの条件を満たすときに限り成立する関係です.作用・反作用の2力は異なる2物体の間で,上記の3つの条件を満たす力が必然的に働き合うものです.
では,何故,作用・反作用の力が働きあうのでしょうか?その答えはやはり素粒子レベルの現象に帰着されます.素粒子の4つの相互作用では作用・反作用の法則がやはり成立します.マクロな現象での力はミクロレベルの重力と電磁力が原因ですが,そのミクロレベルにおいて作用・反作用の法則が成立するのです.例えば,手で壁を押す場合,手と壁は原子・分子からできています.その原子・分子はミクロレベルにおいて作用・反作用を及ぼし合っています.(この場合は電磁力の作用・反作用です.)その原子・分子が集まって,マクロレベルの物体の間,すなわち手と壁の間に作用・反作用が働き合うのです.