Part1 力学の成立

Chapter1 運動

1.1 等速直線運動と等加速度直線運動

力学は，物体の運動，あるいは物体にはたらく力，エネルギー等について取り扱います．このChapterでは，運動について見ていくことにします．

　最初に，簡単のため直線運動を見ていくことにしましょう．直線上を動いた距離，あるいは移動距離を $ \ell[m]$ で表します．移動距離は，大きさだけの量，すなわちスカラーですが，向きを加えた物理量を変位 $ x[m]$ といいます．変位は，最初の位置から最後の位置を結んだ矢印で表すことができます．変位は，大きさと向きを持った量，ベクトルです．直線上を一方方向に運動する場合は，問題ありませんが，Uターンする運動の場合は注意が必要です．途中の経路と関係なく，この場合も，最初の位置と最後の位置を結んだ矢印が変位になります．

変位1

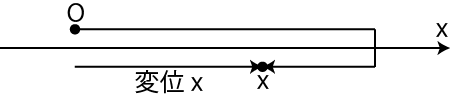
Figure1.1: 変位1

　運動を表す速さという物理量を，単位時間当たりの移動距離で定義します．

定義1.1(直線運動の平均の速さ)

$\displaystyle v\equiv\dfrac{\ell}{t}$

ただし，$ t[s]$ 間に $ \ell[m]$ 進んだ場合を考えました．速さは定義される物理量です．定義とは約束という言葉で言い直すことも可能です．何故，速さが単位時間当たりの移動距離なのかという理由は，そのように定義されたから，約束されたからということです．速さを定義すると運動を取り扱うことができるのです．速さを定義しなければ，その先に進むことができません．全ての物理量は定義されます．物理学とは定義された物理量の間の関係を方程式で表した法則や原理を明らかにしていく学問だと言えるでしょう．速さは，大きさだけの量，すなわちスカラーですが，速さに向きを加えたベクトルの物理量を速度 $ v[m/s]$ といいます．（速さと同じ文字を使います．）速度の定義は，単位時間当たりの変位です．

定義1.2(直線運動の平均の速度1)

$\displaystyle v\equiv\dfrac{x}{t}$

ただし，$ t[s]$ 間に $ x[m]$ 変位した場合を考えました．

　最も簡単な運動の状態としては，静止が挙げられますが，これについては特に言及することもないでしょう．次に簡単な運動の状態として，直線運動の中で，一定の速度で運動する等速直線運動が挙げられます．

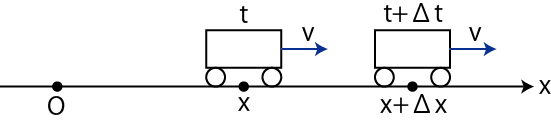
等速直線運動1

Figure1.2: 等速直線運動1

等速直線運動の $ v-t$ グラフと，$ x-t$ グラフを描いておきます．

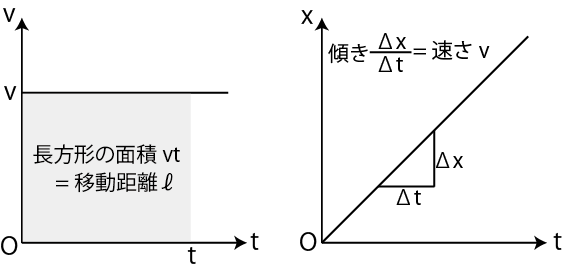
等速直線運動2

Figure1.3: 等速直線運動2

$ v-t$ グラフの長方形の面積は，移動距離 $ \ell[m]$ になり，$ x-t$ グラフの直線の傾きは，速さ $ v[m/s]$ になります．

　速度が変化する運動を取り扱うためには，速度が時間に対して変化する割合である加速度という物理量を考えます．加速度 $ a[m/s^{2}]$ とは，単位時間当たりの速度の変化量であると定義されます．

定義1.3(直線運動の平均の加速度)

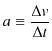
$\displaystyle a\equiv\dfrac{\Delta v}{\Delta t}$

ただし， $ \Delta t[s]$ の時間の間に対する速度の変化量を $ \Delta v[m/s]$ としています．

　等速直線運動の次に簡単な運動は，一定の加速度で直線運動する等加速度直線運動です．状況を図に示しておきます．

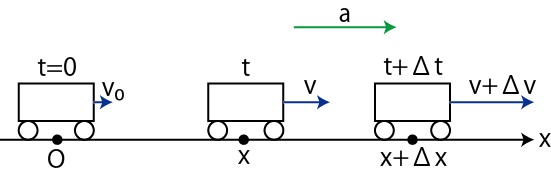
等加速度直線運動1

Figure1.4: 等加速度直線運動1

$ t=0[s]$ で，原点を通るときの速度を，初速度 $ v_{0}[m/s]$，一定の加速度を $ a[m/s^{2}]$ としておきます．等加速度直線運動の $ v-t$ グラフを描いておきます．

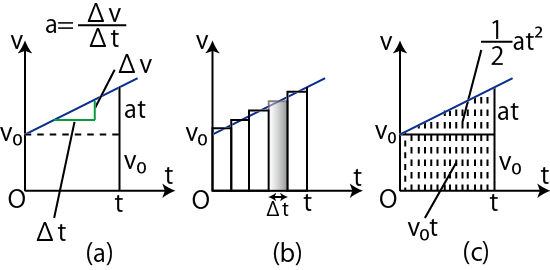
等加速度直線運動2

Figure1.5: 等加速度直線運動2

図の(a)から，$ v-t$ グラフの傾きは，一定の加速度 $ a[m/s^{2}]$ を表すことが理解でき，時間 $ t[s]$ における速度 $ v[m/s]$ は，

$\displaystyle v=v_{0}+at$

となることが確認されます．また，図の(b)のように，短い時間間隔 $ \Delta t[s]$ で区切っていくと，その間では等速直線運動と近似されますので，長方形の面積の和が移動距離になります． $ \Delta t[s]$ を $ 0[s]$ に近づける極限で，グラフのデコボコはなくなり，移動距離は図の(c)のように台形の面積になります．今，考えているような一方方向への直線運動の場合，移動距離は変位 $ x[m]$ に一致しますので，変位 $ x[m]$ は，

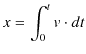
$\displaystyle x=\int_{0}^{t}v\cdot dt$

と積分を使って表すことができます．この場合は，積分を使わなくても面積は，図の(c)のように簡単に求められます．したがって，

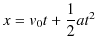
$\displaystyle x=v_{0}t+\dfrac{1}{2}at^{2}$

が成立します．速度の式と変位の式から，時間を含まない3番目の関係式を導くことができます．速度の式より，

$\displaystyle t=\dfrac{v-v_{0}}{a}$

となります．これを変位の式に代入して計算していきます．

$\displaystyle x=v_{0}\dfrac{v-v_{0}}{a}+\dfrac{1}{2}a(\dfrac{v-v_{0}}{a})^{2}$

したがって，

$\displaystyle 2ax$ $\displaystyle =2v_{0}(v-v_{0})+(v-v_{0})^{2}$    
  $\displaystyle =2v_{0}v-2v_{0}^{2}+v^{2}-2vv_{0}+v_{0}^{2}$    
  $\displaystyle =v^{2}-v_{0}^{2}$    

となりますので，時間を含まない関係式，

$\displaystyle v^{2}-v_{0}^{2}=2ax$

が成立します．

 

1.2 一般の直線運動

$ x$ の正の方向に加速度 $ a[m/s^{2}]$ で運動する直線運動を図に示しておきます．

直線運動

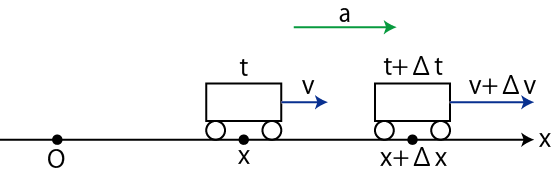
Figure1.6: 直線運動

図の時間 $ \Delta t[s]$ の間の変位は， $ \Delta x[m]$ です．さて， $ \Delta t[s]$ 間の平均の速度 $ v[m/s]$ は次のように表されます．

定義1.4(直線運動の平均の速度2)

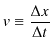
$\displaystyle v\equiv\dfrac{\Delta x}{\Delta t}$

$ \Delta t[s]$ を無限小にする極限をとると，この式の値は瞬間の速度となります．これを改めて $ v[m/s]$ とおくと，

定義1.5(直線運動の瞬間の速度)

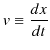
$\displaystyle v\equiv\dfrac{dx}{dt}$

となります．つまり，速度は変位を時間で微分した量です．また，平均の加速度 $ a[m/s^{2}]$ は次のように表されました．

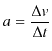
$\displaystyle a=\dfrac{\Delta v}{\Delta t}$

ここで， $ \Delta v[m/s]$ は $ \Delta t[s]$ の間の速度の変化量です． $ \Delta t[s]$ を無限小にする極限をとると，この式は瞬間の加速度を表します．これを改めて $ a[m/s^{2}]$ とおくと，

定義1.6(直線運動の瞬間の加速度)

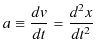
$\displaystyle a\equiv\dfrac{dv}{dt}=\dfrac{d^{2}x}{dt^{2}}$

となります．したがって，加速度は速度を時間で微分した量，あるいは変位を2回時間で微分した量です．

　では逆に加速度から速度を，速度から変位を求めてみましょう．まず，加速度から速度を求めてみます．

速度

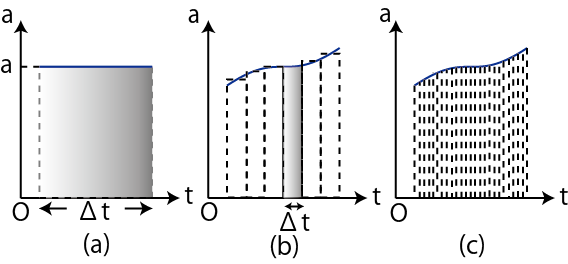
Figure1.7: 速度

一定の加速度 $ a[m/s^{2}]$ の等加速度直線運動という特別な場合を考えます．このとき，速度の変化量は $ a\Delta t[m/s]$ です．$ a-t$ グラフは $ a[m/s^{2}]$ が一定で，$ t$ 軸に平行な直線になりますが，速度の変化量はこのグラフの長方形の面積になります．（図 "速度" の(a)のグラフを参照して下さい．）一般に加速度が変化する場合では，グラフをある短い時間間隔 $ \Delta t[s]$ で幾つかの区間に分割します．その区間において加速度の平均値をとり，有限個の長方形をつくります．各区間において速度の変化量は長方形の面積で近似されます．したがって，全体の速度の変化量は長方形の面積の和になります．（図 "速度" の(b)を参照して下さい．）ここで， $ \Delta t[s]$ を無限小にする極限をとると，無限個の細長い長方形でグラフは分割され，グラフのでこぼこはなくなり，速度の変化量は無限個の細長い長方形の和になります．（図 "速度" の(c)を参照して下さい．）つまり，加速度が変化する場合でも速度の変化量は $ a-t$ グラフの面積であり，これは加速度 $ a[m/s^{2}]$ を時間 $ t[s]$ で積分したものです．故に，速度 $ v[m/s]$ は積分定数を初速度と考えて，次式で表されます．

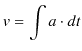
$\displaystyle v=\int a\cdot dt$

同様に，速度から変位を求めてみましょう．

変位2

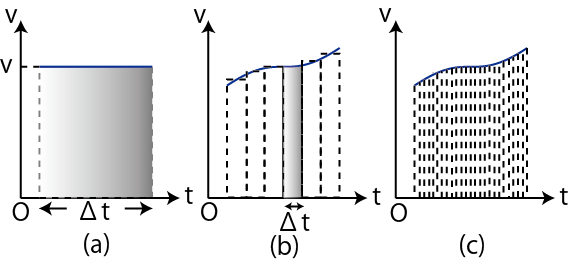
Figure1.8: 変位2

一定の速度 $ v[m/s]$ の等速直線運動という特別な場合を考えます．このとき，変位は $ v\Delta t[m]$ です．$ v-t$ グラフは $ v[m/s]$ が一定で，$ t$ 軸に平行な直線になりますが，変位はこのグラフの長方形の面積になります．（図 "変位2" の(a)のグラフを参照して下さい．）一般に速度が変化する場合では，グラフをある短い時間間隔 $ \Delta t[s]$ で幾つかの区間に分割します．その区間において速度の平均値をとり，有限個の長方形をつくります．各区間において変位は長方形の面積で近似されます．したがって，全体の変位は長方形の面積の和になります．（図 "変位2" の(b)を参照して下さい．）ここで， $ \Delta t[s]$ を無限小にする極限をとると，無限個の細長い長方形でグラフは分割され，グラフのでこぼこはなくなり，変位は無限個の細長い長方形の和になります．（図 "変位2" の(c)を参照して下さい．）つまり，速度が変化する場合でも変位は $ v-t$ グラフの面積であり，これは速度 $ v[m/s]$ を時間 $ t[s]$ で積分したものです．故に，変位 $ x[m]$ は次式で表されます．

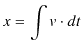
$\displaystyle x=\int v\cdot dt$

　等加速度直線運動の場合に成立する関係式を導いておきましょう．ただし，初期条件は $ t=0[s]$ で $ v=v_{0}[m/s],x=0[m]$ と与えておきます．まず，

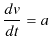
$\displaystyle \dfrac{dv}{dt}=a$

の式からスタートします．加速度が一定の場合を考えていますので， $ a[m/s^{2}]$ は定数です．両辺を時間 $ t[s]$ で一回積分すると，

$\displaystyle v=at+C$

となります．（$ C$ は積分定数．）ここで，$ t=0[s]$ で， $ v=v_{0}[m/s]$ の条件を代入すると，

  $\displaystyle v_{0}=a\times0+C$    
% latex2html id marker 1273 $\displaystyle \therefore$ $\displaystyle C=v_{0}[m/s]$    

になります．よって，

$\displaystyle v=v_{0}+at$

の関係式が成立します．もう一度，両辺を時間 $ t[s]$ で積分すると，

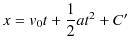
$\displaystyle x=v_{0}t+\dfrac{1}{2}at^{2}+C'$

となります．（$ C'$ は積分定数．）ここで，$ t=0[s]$ で $ x=0[m]$ の条件を代入して，

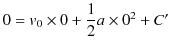  $\displaystyle 0=v_{0}\times0+\dfrac{1}{2}a\times0^{2}+C'$    
% latex2html id marker 1288 $\displaystyle \therefore$ $\displaystyle C'=0$    

です．故に，

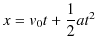
$\displaystyle x=v_{0}t+\dfrac{1}{2}at^{2}$

が成立します．逆に，この式を時間 $ t[s]$ で1回微分すると，

$\displaystyle v=v_{0}+at$

が導かれ，さらにもう1回時間 $ t[s]$ で微分すると，

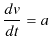
$\displaystyle \dfrac{dv}{dt}=a$

となることが確かめられます．

 

1.3 曲線運動

一般の曲線運動を取り扱ってみましょう．状況を図示すると図のようになります．

曲線運動

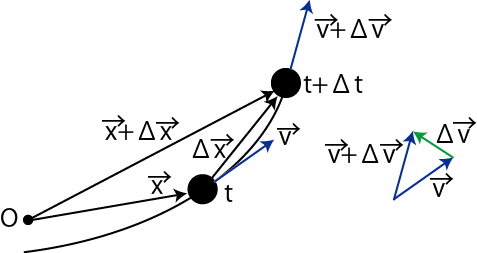
Figure1.9: 曲線運動

この場合，平均の速度 $ \vec{v}[m/s]$ は次のように表されます．

定義1.7(曲線運動の平均の速度)

$\displaystyle \vec{v}\equiv\dfrac{\Delta\vec{x}}{\Delta t}$

ここで， $ \Delta t[s]$ はある有限の時間， $ \Delta\vec{x}[m]$ は $ \Delta t[s]$ の間の変位です．（曲線運動の場合も，変位とは途中の経路と無関係に，考えている最初の位置と最後の位置を結んだ矢印になります．） $ \Delta t[s]$ を無限小にする極限をとると，この式の値は瞬間の速度になります．これを改めて $ \vec{v}[m/s]$ とおき直すと，

定義1.8(曲線運動の瞬間の速度)

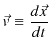
$\displaystyle \vec{v}\equiv\dfrac{d\vec{x}}{dt}$

です．つまり，速度は変位を時間で微分した量です．また，平均の加速度 $ \vec{a}[m/s^{2}]$ は次のように表されます．

定義1.9(曲線運動の平均の加速度)

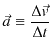
$\displaystyle \vec{a}\equiv\dfrac{\Delta\vec{v}}{\Delta t}$

ここで， $ \Delta t[s]$ はある有限の時間， $ \Delta\vec{v}[m/s]$ は $ \Delta t[s]$ の間の速度の変化量です． $ \Delta t[s]$ を無限小にする極限をとると，この式の値は瞬間の加速度になります．これを改めて $ \vec{a}[m/s^{2}]$ とおくと，

定義1.10(曲線運動の瞬間の加速度)

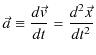
$\displaystyle \vec{a}\equiv\dfrac{d\vec{v}}{dt}=\dfrac{d^{2}\vec{x}}{dt^{2}}$

となります．したがって，加速度は速度を時間で微分した量，あるいは変位を2回時間で微分した量です．

 

1.4 速度の合成と分解

2つの速度を合成することを考えましょう．例えば，状況としては動いている列車の中で走っている人の速度を求めるような場合です．列車の速度 $ v_{1}[m/s]$ と，列車に対する人の速度 $ v_{2}[m/s]$ の合成速度 $ v[m/s]$ を求めましょう．そのためには，速度というものが $ 1[s]$ 間の変位であることを思い出します．$ 1[s]$ の間に列車は $ v_{1}[m]$ 動き，その列車に対して人は $ v_{2}[m]$ 動きます．したがって，$ 1[s]$ 間に，人が地面に対して動いた変位は，

$\displaystyle v[m]=v_{1}[m]+v_{2}[m]$

となります．$ 1[s]$ あたりの変位は，速度の定義ですから，これがそのまま合成速度の式になります．

$\displaystyle v[m/s]=v_{1}[m/s]+v_{2}[m/s]$

一直線上の速度の向きを正と負で表すことができますから， $ v,v_{1},v_{2}[m/s]$ は負の値もとることができます．

　斜め方向の2つの速度を合成する問題を考えましょう．速度はベクトルですから，ベクトルの合成の方法である平行四辺形の作図によって，合成されます．しかし，おそらく，ベクトルという数学的概念が先にあった訳ではなく，速度とか力といった物理的な量が研究され，それがベクトルという抽象化された数学的実体となったと考えられます．ですから，速度の合成は数学的にではなく，物理的に理解する必要があります．

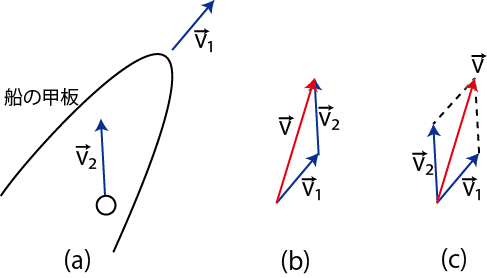
速度の合成と分解

Figure1.10: 速度の合成と分解

速度の合成を考える上で，簡単な状況として，運動する船の甲板上にある運動する物体というものを設定しましょう．船が $ \vec{v}_{1}[m/s]$ で運動し，その船に対して物体が $ \vec{v}_{2}[m/s]$ で運動する場合です．一直線上の運動の場合と同じように，速度が $ 1[s]$ 間の変位であることを使いましょう．$ 1[s]$ 間に，船は $ \vec{v}_{1}[m]$ だけ動き，物体は船に対して $ \vec{v}_{2}[m]$ だけ動きます．したがって，物体の運動を岸から見ると，$ 1[s]$ 間に，図の(b)のようになります．すなわち，まず $ \vec{v}_{1}[m]$ だけ船が変位し，その船の変位に $ \vec{v}_{2}[m]$ を加える訳ですから， $ \vec{v}_{1}[m]$ の終点に $ \vec{v}_{2}[m]$ の始点をもってきて， $ \vec{v}_{1}[m]$ の始点から $ \vec{v}_{2}[m]$ の終点への矢印が，合成された $ 1[s]$ あたりの変位 $ \vec{v}[m]$ になります．$ 1[s]$ あたりの変位は速度の定義ですから，この図の(b)の関係は，そのまま，速度の関係になります．つまり，速度 $ \vec{v}_{1}[m/s]$ と，速度 $ \vec{v}_{2}[m/s]$ の合成速度は， $ \vec{v}[m/s]$ になります．ここで， $ \vec{v}_{2}[m/s]$ を平行移動して始点を揃えると，平行四辺形の図(c)になります．したがって，合成速度は平行四辺形の対角線となるのです．この状況をベクトルの数式で表すと，

$\displaystyle \vec{v}[m/s]=\vec{v}_{1}[m/s]+\vec{v}_{2}[m/s]$

となります．

　速度の分解は合成の逆です．図の(c)の平行四辺形で赤矢印の合成された速度を，青矢印のもとの速度に戻せばよいのです．速度を分解する際，分解の方向は任意であって，異なる二方向であれば，分解することができます．

 

1.5 相対速度

通常，速度と言ったとき，基準である地面から見た場合の絶対的な速度を指します．それに対して，お互いに運動している物体が一方から他方を見たときの速度を相対速度と言います．

　一直線上の運動の場合，前Sectionの速度の合成の式，

$\displaystyle v=v_{1}+v_{2}$

において， $ v_{1}[m/s]$ は地面から見た列車の速度， $ v_{2}[m/s]$ は列車に対する人の速度，$ v[m/s]$ は地面から見た人の速度です．ここで， $ v_{2}[m/s]$ は列車から見た人の相対速度になっていることに注意しましょう．

$\displaystyle v_{2}=v-v_{1}$

となりますから，相対速度を求めるルールとしては，観測者の速度（この場合，列車の速度．）を引くということになります．

　斜め方向のの運動の場合，前Sectionの速度の合成の式，

$\displaystyle \vec{v}=\vec{v}_{1}+\vec{v}_{2}$

において， $ \vec{v}_{1}[m/s]$ は岸から見た船の速度， $ \vec{v}_{2}[m/s]$ は船から見た物体の速度， $ \vec{v}[m/s]$ は岸から見た物体の速度です．ここで， $ \vec{v}_{2}[m/s]$ は船から見た物体の相対速度になっていることに注意しましょう．

$\displaystyle \vec{v}_{2}=\vec{v}-\vec{v}_{1}$

となりますから，相対速度を求めるルールとしては，一直線上の運動の場合と同じく，観測者の速度を引くということになります．1から見た2の相対速度を $ \vec{v}_{12}[m/s]$ と書くことにすると，

$\displaystyle \vec{v}_{12}=\vec{v}_{2}-\vec{v}_{1}$

と書き直すことができます．